基于有限元的某汽车排气系统模态分析及悬挂点的优化

（潍柴动力股份有限公司上海研发中心，上海201315）

基于有限元的某汽车排气系统模态分析及悬挂点的优化

郭深深，王云英，乔海周

（潍柴动力股份有限公司上海研发中心，上海201315）

在整车开发前期，为了尽可能减小排气系统悬挂点位置对整车NVH性能的影响，采用有限元分析的方法对某汽车排气系统的振动模态进行分析，同时利用平均驱动自由度法（ADDOFD）对系统悬挂点位置进行优化。研究结果显示：在汽车开发前期，采用ADDOFD法进行排气系统悬挂点位置的优化布置是有必要的。所做仿真分析研究对于缩短整车开发周期、节约成本、优化性能有重要意义。

排气系统模态分析悬挂点优化有限元分析平均驱动自由度法

1 引言

随着人们生活水平的提高和汽车工业的不断发展，人们对汽车的要求也越来越高，结构紧凑、宽敞舒适、NⅤH性能良好的汽车产品普遍受到欢迎。

汽车排气系统一般通过法兰和吊耳与发动机歧管及车身底板相连。在汽车的使用过程中，排气系统由于受到发动机振动和排气激励的影响，会产生较大的振动，而振动能量通过悬挂点传递至车身底板，引起车身振动并产生车内噪声。与此同时，在整车开发后期，由于油箱、底板、悬架的布置往往会造成吊耳的悬挂点无法满足整车NⅤH性能的要求。因此，在整车开发前期对排气系统振动进行分析，优化吊耳悬挂点的位置，以减少车身振动及噪声水平，是排气系统设计时需要重点关注的方面[1,2]。

对排气系统振动问题的早期研究方法是试验法，即通过试验手段进行排气系统与整车NⅤH性能的匹配，这种方法研究周期长且成本较高。本文利用排气系统三维数模及质量分布情况，借助有限元分析软件对排气系统进行振动仿真及模态分析，在整车开发前期实现吊耳悬挂点位置的优化选择，降低排气系统振动对车内噪声及驾乘舒适性的影响，同时缩短研发周期，降低研发成本，这对整车开发及NⅤH性能的优化具有重要的意义。

2 模态分析理论

2.1模态分析的理论基础

对于一个n个自由度线性的定常系统，其基本振动方程可写成[3,4]：

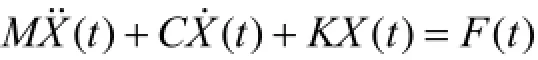
其中，M为系统的质量矩阵，C为阻尼矩阵，K为刚度矩阵，X(t)为加速度向量，X(t)为速度，F(t)为动激励载荷向量。

机构动力特性分析是属于经典的模态分析领域，通过分析能确定结构的各阶固有频率、各阶振型及阻尼，而结构的固有频率和振型是分析结构动力学响应及其他动力特性问题的基础。在进行模态分析时，一般因结构阻尼较小，对固有频率和振型影响甚微，故通常忽略不计。于是，任何一个无阻尼线性弹性结构振动系统自由振动运动方程可表示为：

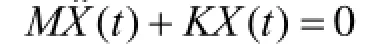
在此情况下，分析结构的固有频率与振型问题就转化为求解方程的特征值与特征向量问题。

2.2平均驱动自由度位移法（ADDOFD）

假设单点激励，由多自由度系统模态分析理论，响应点l和激励点p之间的频率响应函数为[5,6]：

其中，φlr是第l个测点，第r阶模态振型系数，Mr和ξr分别是模态质量和模态阻尼比。如果激励力的频率为ωr，则近似地有：

对于线性系统，位移响应的幅值和频率响应函数的幅值成正比，即

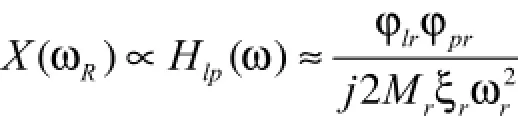
假设振型以质量矩阵归一化，各阶模态阻尼近似相等，则

可定义第j个自由度的平均去顶自由度位移（ADDOFD）为

ADDOFD(j)可获得某个自由度在一般激励情况下的（在某个频率范围内所有模态均被激发）的位移响应相对大小，以此对排气系统吊耳悬挂点的位置进行优化选择。

3 某车型排气系统模态分析

3.1 有限元模型的建立

该车型排气系统由以下几部分组成：波纹管、三元催化器、后消音器、排气管路及联接法兰。由于排气系统结构较为复杂，在建立有限元模型时对系统进行适当程度的简化：（1）法兰简化为体单元；（2）三元催化器及后消音器简化为集中质量单元，集中质量单元位于三元催化器和后消音器的几何中心；（3）波纹管简化为CBUSH弹簧联接单元。

模型参数如下：三元催化器前法兰厚度10 mm，三元催化器后法兰厚度6 mm，三元催化器及后消音器壁厚1.2 mm，其余管路部分厚度均为1.5 mm，材料弹性模量E=2.1×105MPa，泊松比μ=0.3，密度ρ=7.9×10-3g/mm3，CBUSH弹簧单元在X、Y、Z三个方向刚度为Kx=20，Ky=1，Kz=1。有限元模型见图1。

图1 排气系统有限元模型

3.2系统模态分析

不考虑排气系统原悬挂、支撑及排气歧管约束对排气系统振动的影响，对排气系统自由模态进行分析。通过对自由模态的分析，求解排气系统固有振动属性，为整车NⅤH性能匹配提供依据。该车型所配的发动机转速范围0～3 300 r/min，通过计算可以得到发动机激励频率范围0～110 Hz。即在自由状态下只需对0～110 Hz频率范围内排气系统各阶模态进行分析。

表1列出了排气系统各阶固有频率，由于1-9阶频率很小，排气系统是刚性体，可以认为是离散刚体的固有频率，其并未显示在表1中。在发动机0～110 Hz激励频率下，仅对10～19阶振型进行分析。

选取排气系统几个典型自由模态（11阶、15阶、17阶、18阶）位移分布云图见图2。

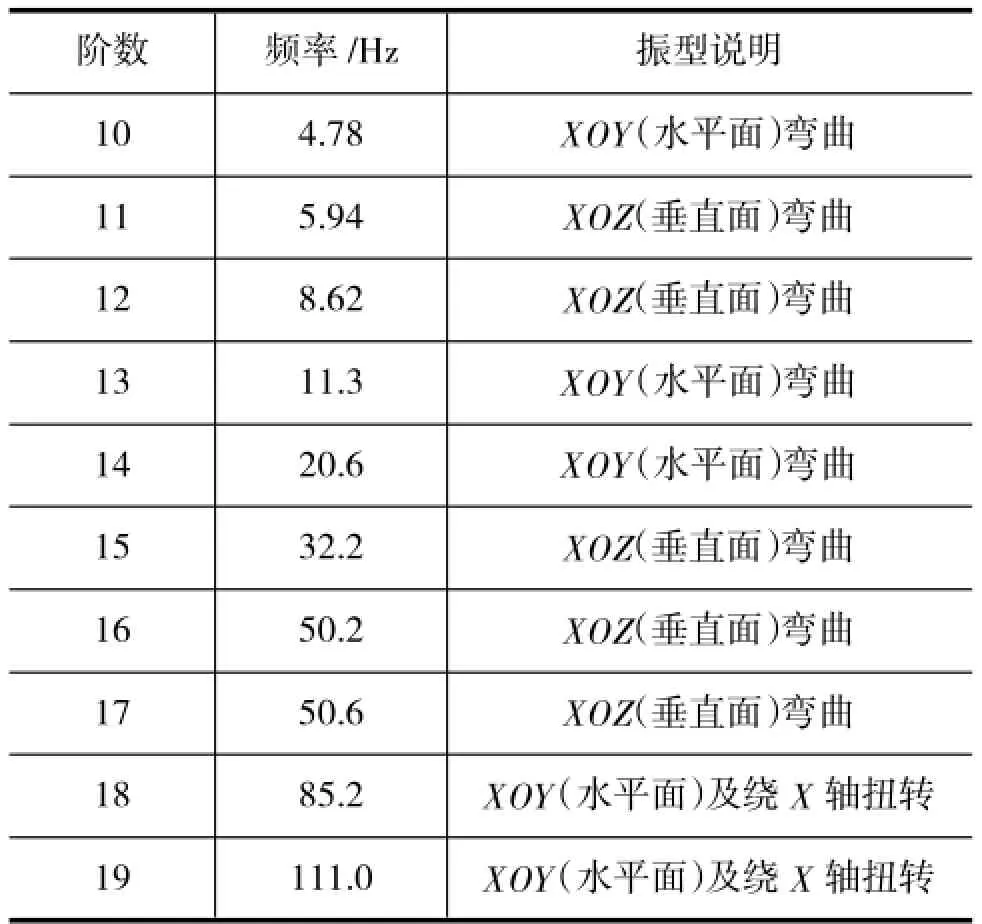
表1 模态分析结果

图2 排气系统有限元模型

由图2可以看出，各阶模态振动位移各有不同，11阶模态的波纹管前位置相对位移较小，而三元催器与后消音器相对位移较大；15阶后消音器整体相对位移偏小，尾管拐弯处相对位移较大；17阶模态波纹管前段相对位移较大，而尾管相对位移较小；18阶波纹管之前相对位移较小，波纹管之后相对位移较大，而且存在扭转现象。

根据以上模态分析，在选择最优悬挂点时，因综合考虑各阶模态（11～19阶），将悬挂点布置在综合相对位移较小的位置。

4 排气系统悬挂位置的优化选择

4.1悬挂位置选择的原则

排气系统悬挂位置选择一是考虑质量分布，即在系统中的质量集中位置安装悬挂点，如三元催化器、消音器前/后附近的位置[7]。

其二是悬挂点位于系统XOZ（垂直平面）方向主要振型节点位置。排气系统弯曲振动主要发生在XOY平面（水平面）及XOZ平面（垂直平面），排气系统吊挂点垂直安装的情况下，XOY平面弯曲振动传递到车架及车身的振动力影响很小，因此在吊挂点布置时，主要考虑位于XOZ内弯曲振动节点附近。

4.2悬挂点位置的选择

基于质量分布的悬挂位置选择原则，在排气系统中，选择可能的所有悬挂点位置（包括现悬挂位置），进行标号。该车型排气系统可能的悬挂位置见图3，一共13悬挂点位置，其中4、7、8、12为原设计的4个悬挂位置。

根据平均驱动自由度位移法（ADDOFD）计算各悬挂位置在XOZ方向的位移比值，计算结果见图4。位置点4、7、8、10、13为XOZ方向振动节点位置，即为该车型改进后的排气系统五个最优悬挂点位置。与原悬挂位置4、7、8、12相比，即在消音器后端增加挂点10，并将尾管处悬挂点12移至靠近尾管出口的悬挂位置13。

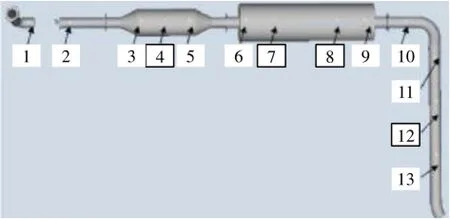
图3 排气系统可能的悬挂位置

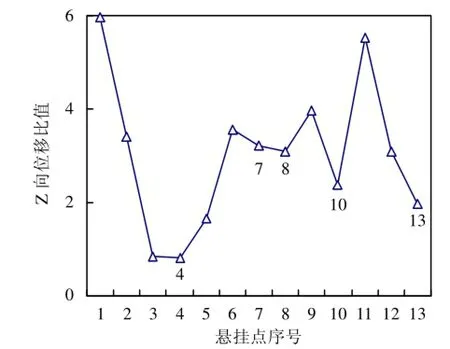
图4 各悬挂位置Z向位移比值曲线图

5 悬挂点优化前后车内噪声测试对比与分析

排气系统通过法兰与吊耳与排气歧管及驾驶室底板连接，由于发动机本身振动及排气激励的影响，振动较大并通过悬挂点传向车身，引起较大的车内噪声[8]。

参考GB 18697－2002标准，按照图5中的测点对该车辆进行怠速工况和二档加速工况车内噪声测试。测试悬挂点优化前后怠速工况时车内各测点声压级，测试结果对比见图6。

测点4噪声降幅较大，其二档加速工况噪声测试结果见图7。由图6、图7可知，怠速工况下，车内各测点噪声均明显降低，其中，后排测点4、测点5噪声降幅较大。优化后，测点1、测点2噪声略高于目标值，测点3、测点4、测点5噪声均优于目标值。

图5 车内噪声测点位置示意图

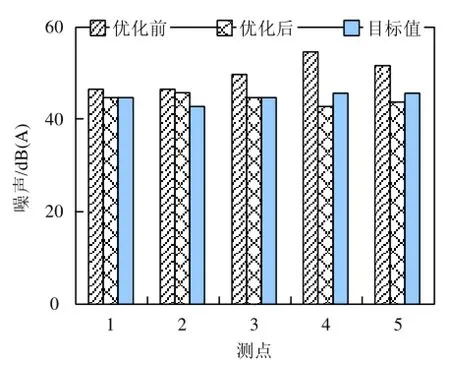
图6 优化前后怠速工况各测点声压级对比

图7 优化前后二挡加速工况测点4声压级对比

在二档加速工况，测点4优化后的噪声值下降较多，在测试转速范围内，噪声呈波动式增长，除个别转速处噪声值略高于目标值，其余测试转速区域噪声优化效果明显。

6 结束语

本文基于有限元分析的方法对排气系统进行振动模态分析，获取系统的固有频率及振型信息。同时，基于平均驱动自由度位移法（ADDOFD）对排气系统悬挂位置进行优化选择，可以在整车开发前期缩短研发周期、降低研发成本，并有助于提高整车NⅤH性能。

采用以上方法对某车辆排气系统悬挂点进行优化，将悬挂点设置在振动节点处。测试结果显示，优化后车内噪声明显下降。其中，怠速工况时前排车内噪声平均下降2 dB(A)，后排噪声平均下降5 dB(A)；二档加速工况时噪声平均下降达到4 dB (A)，测试转速范围内最大降幅达到6 dB(A)。

1傅志方，华宏星.模态分析理论与研究[M].上海：上海交通大学出版社，2000.

2张胜兰，郑冬黎.基于HyperWorks的结构优化设计技术[M].北京：机械工业出版社，2007.

3杨万里，陈燕，邓小龙.乘用车排气系统模态分析数值模拟研究[J].三峡大学学报：自然科学版，2005.

4王继先，李兆文.内燃机排气系统振动特性分析[J].内燃机工程，2008.

5赵海澜，顾彦.汽车排气系统悬挂点优化[J].计算机辅助工程，2006.

6李松波.车辆排气系统振动建模与动力学特性研究[D].上海交通大学，2008.

7徐献阳，李松波，张建武.某轿车排气系统振动特性仿真及优化[J].设计与研究-机械，2008.

8 Lee C M,Park S T.Development of a Simple Numerical Method of the Exhaust System to Find Optimized Design Values[DO/OL].SAE, 2000(1):0117.

Ⅴibration Model Analysis of Automobile Exhaust System andⅠts Hanging Location Optimization

Guo Shenshen,Wang Yunying,Qiao Haizhou
（Weichai Power Co.,Ltd.,Shanghai R&D Center,Shanghai 201315,China）

Ⅰn order to reduce the impact of exhaust system vibration on vehicle NⅤH performance at the early stage of a vehicle design,finite element analysis is used to perform finite modeling and vibration modal analysis on a vehicle's exhaust system.Furthermore,a method called average driving DOF displacement (ADDOFD)is used to optimize hanging locations.The result suggests that the ADDOFD method is an effective method for determining hanging locations of exhaust system in the early stage of a vehicle design. Therefore,the simulation analysis presented in this paper could save both time and cost in developing a new vehicle.

exhaust system,vibration modal analysis,hanging location optimization, finite element method,ADDOFD method

10.3969/j.issn.1671-0614.2014.04.004

来稿日期：2014-07-14

郭深深（1987-），男，本科，主要研究方向为排气系统设计及有限元分析。