基于装配自由度分析解决欠约束问题

王 浪， 张京英， 杨 薇， 樊 琼

（北京理工大学机械与车辆学院，北京 100081）

基于装配自由度分析解决欠约束问题

王 浪， 张京英， 杨 薇， 樊 琼

（北京理工大学机械与车辆学院，北京 100081）

装配是机械制造过程中的一个重要环节，在装配过程中，经常会遇到欠约束问题。在复杂装配环境下，某个装配零件的欠约束会对其他零件的装配产生意想不到的结果。装配时，约束条件和零件自由度之间存在一种内在联系，通过建立基体和目标零件的自由度空间坐标系，对约束条件和自由度关系分析，得到约束条件和自由度关系的逻辑值，通过逻辑值判断剩余自由度的个数和类型，从而为快速解决欠约束问题提供了一种途径。

欠约束；自由度分析；逻辑值；装配；空间坐标系

装配是机械制造过程中的一个重要环节。产品装配所需工时占产品生产制造总工时的40%～60%[1]。装配求解问题是三维几何造型中的基本问题，其实质是约束满足问题，即通过一组几何装配约束推理求得实体的空间位置和方向[2]。

欠约束是指零件在装配时，没有被完全约束，能在某个方向运动。在装配体比较简单时，欠约束问题不明显，但是在大型复杂的装配体中，如果某个零件存在欠约束，那么以此零件表面为约束条件的零件以及其他相关的零件就会在装配时发生错乱，产生意想不到的结果，这就是欠约束问题带来的麻烦。欠约束问题经常体现在轴与孔的装配约束中，当某个螺钉需要装配在板件的孔上时，通常采用轴对齐和贴合两种约束方式就能在外观上达到基本的装配要求，但螺钉还是可以绕轴线旋转，这就是欠约束。传统上习惯的做法是置之不理，因为零件已经达到基本的装配要求。如果要解决这个欠约束，传统通常是在螺钉和板件上新建两个平面，利用平面约束关系来限制螺钉的转动，但在大型复杂的装配体中操作非常繁琐。

针对欠约束问题，为使得零件完全被约束，本文通过建立自由度空间坐标系，找出自由度和约束条件的相互关系，得到逻辑值，为快速解决欠约束问题提供了一条有效的途径。

1 刚体自由度和常见约束类型归类

1.1 刚体自由度

自由度分析法是一项用以求解一组刚体的位置和方向以满足特定几何约束的技术[3]。自由度是确定一个几何体或系统所必需的独立的坐标或参数的个数[4]。一个刚体在空间任意运动时，可分解为 3个平动自由度和 3个转动自由度。如图1所示，在空间坐标系中，一个没有受到平任动何自约由束度的可刚表体示，为沿、着X，和Y→，, Z绕轴X方，向Y，的Z3个轴方向的3转动自由度可表示为 Rx、 Ry和 Rz。

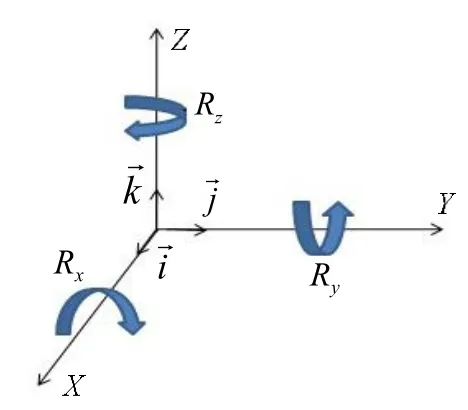
图1 刚体的自由度空间坐标系

1.2 常见约束类型

零件装配的过程实际上就是使被装配的零件逐步满足约束的过程[5]，零件之间的约束是通过两个零件上的几何元素的不同配合来完成的[6]。常见约束类型如表1所示，这些约束类型在本质上是一致的，都是由平面+平面、线+线或平面+线的约束组成，因此，零件装配过程主要是由这3种约束来限制零件的运动，使零件的自由度完全为零。

表1 约束类型

2 建立约束条件和自由度的关系，计算逻辑值

2.1 建立自由度空间坐标系

在零件装配过程中，平面约束和轴约束是装配过程中遇到最多的约束，下面主要对这两种约束类型的自由度进行分析。在零件装配过程中，定义已经被完全约束自由度为零的零件称为基体，建立基体的空间自由度坐标系如图2(a)所示，定义这个基体的空间自由度坐标系为基坐标系，基体自由度为零，但是平动和转动的自由度方向依然存在。定义待装配的零件为目标零件，建立目标零件的空间自由度坐标系如图2(b)所示，目标零件有沿 X1， Y1， Z1轴方向的平动自由度和绕 X， Y， Z轴

111的转动自由度 Rx1、 Ry1、 Rz1。对装配→过程中目标零件自由度的分析就转变为分析 i1、 →j1、 k→1和 Rx1、 Ry1、 Rz1这 6个由自由度构成的矢量相对基坐标系的位置关系。

图2 自由度空间坐标系

2.2 面+面约束和自由度关系的分析与计算

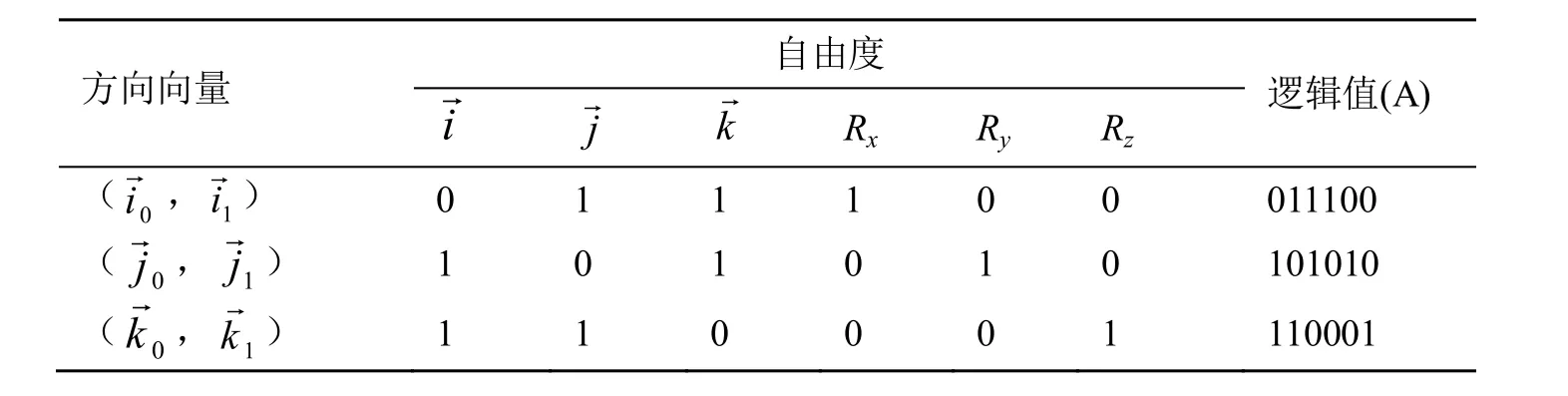
表2 面+面约束和自由度关系

表3 A1、A2和A3逻辑与运算

2.3 线+线约束和自由度关系的分析和计算

表4 线+线约束和自由度关系

表5 B1、B2和B3逻辑与运算

3 复合约束条件和自由度关系的实例分析计算

下面以螺钉和板的装配关系为例说明，将螺钉装入板上的孔中，采用线+线和面+面的联合约束方式对螺钉的自由度进行分析。

使用轴对齐方式使螺钉的轴线和孔的轴线对齐，建立如图3所示的自由度空间坐标系，目标零件的轴线方向向量为孔的轴线的方向向量为，根据表4中可得到如图3所示的结果，图3中的红色×符号表示目标零件螺钉的自→由度被限制住，螺钉只剩下两个自由度，即和 Rz1（一个平动自由度和一个转动自由度），得到的逻辑值为B3=001001。

图3 轴对齐约束方式

使用平面贴合约束方式使螺钉的下表面和板的上表面相贴合，如图4所示建立自由度空间坐 根k→1据，标 表作系 为，2基中目体标(的零 ，板件的螺)上 ，钉表可下面得表的到面方如的向图方向4向量所向为示量的，为结果，图中螺钉处有红色×符号的 3个自由度被限制，只剩下 、 和 Rz13个方向的自由度，得到的逻辑值为A3=110001。

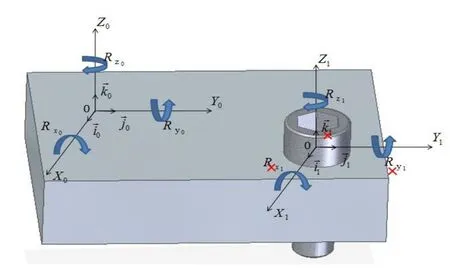
图4 平面贴合约束方式

通过轴对齐和平面贴合的复合约束方式，得到的螺钉的自由度如图5所示，螺钉只剩下Rz1方向的自由度，而采用逻辑值直接进行与运算可得A3·B3=000001，结果中的1表示的是 Rz1方向的自由度，与实际复合约束结果一致。

装配过程中，为使得螺钉完全被约束，自由度为零，还需要利用其他平面的约束方式，使得 Rz1方向的自由度被限制，但是由于目标零件的装配已经达到基本要求，就没必要再重新构建平面，新建约束。对于欠约束，系统可以向用户弹出一个提醒对话框，告知约束不足，同时系统可通过逻辑值的运算，进行(，)或(，)操作，使得逻辑值为 000000，这样目标零件螺钉被完全约束，自由度为零。

图5 复合约束方式

4 结 论

约束条件和自由度之间存在内在联系，通过建立基体和目标零件的自由度空间坐标系，对约束条件和自由度关系进行分析，得到约束条件和自由度关系的逻辑值，逻辑值中1的个数和位置决定了目标零件的自由度的个数和具体类型。在装配过程中，通过控制或来控制目标零件的自由度，使逻辑值为000000，目标零件自由度变为零，目标零件被完全约束，这为快速解决欠约束问题提供了一种有效途径。

[1] 陈万领, 严晓光, 陈卓宁, 宾鸿赞. 面向三维 CAD的装配顺序建模系统研究[J]. 中国机械工程, 2005, 16(20): 1839-1842.

[2] 周 昀, 袁 波, 胡事民, 孙家广. 基于自由度归约分析的装配求解新方法[J]. 计算机辅助设计与制造, 1998, (11): 33-35.

[3] 张红哲, 侯文彬, 胡 平, 李运兴. 模具装配中求解约束的自由度分析算法[J]. 机械设计与制造, 2003, (1): 38-39.

[4] 程志明, 韩兆洲. 自由度的认识与应用[J]. 统计与决策, 2011, (12): 167-169.

[5] 张 翀, 周经野, 韩忠愿. 基于自由度分析的装配体约束求解[J]. 湘潭大学自然科学学报, 2006, 28(1): 41-45.

[6] 彭 享, 郭连水. 自由度描述与装配约束图求解方法的研究[J]. 机械工程师, 2007, (12): 57-59.

Resolution of Under-Constraint Problem Based on DOF Analysis During Assembly Process

Wang Lang, Zhang Jingying, Yang Wei, Fan Qiong
(School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China )

Assembly is an important part in the process of mechanical manufacturing. Under-constraint often exists in the assembly process. If a part is in an under-constraint situation during a large and complex assembly process, it will bring an unexpected result to the related parts which take the surface of the part as constraint reference. To solve the under-constraint problem, the relationship between degrees of freedom (DOF) and constraints is established by building space coordinate system. Logical values can be obtained from the tables. The numbers and types of DOF are determined by logical values, and it provides a quick method to solve the under-constraint problem.

under-constraint; DOF analysis; logical value; assembly; space coordinate system

TP 391.72

A

2095-302X (2014)02-0226-04

2013-04-18；定稿日期：2013-06-13

王 浪（1989-），男，湖北武汉人，硕士研究生。主要研究方向为机械设计。E-mail：603787864@qq.com