汽轮机转子挠曲对可倾瓦轴承油膜特性的影响
曹康琪越
(大唐长春第二热电有限责任公司,长春 130000)
目前,汽轮机可倾瓦滑动轴承轴瓦油膜的失稳现象频繁发生,旋转机械难以达到额定性能指标,严重影响到汽轮机组安全经济运行[1-2]。为了解决这一问题,高庆水等[3]在分析圆柱轴承压力特性时首次使用了Fluent数值模拟,论证了各种方法计算结果与实际的误差大小,但是没能给出一个研究其他滑动轴承的最优数值模拟方法;涂林等[4]在使用Fluent中的RNGk-ε模型模拟油膜特性时修正了湍动黏度,使模拟结果更接近实际值,但是对于小间隙的油膜流场计算误差较大。张楚等[5]基于气液两相流原理模拟计算油膜特性,得出了滑动轴承油膜分布规律,但是该方法不能很好的计算流体本身的流动特性。Matthew Cha[6]等利用数值模拟方法对雷诺方法进行有限元求解,分析了支点对可倾瓦滑动轴承非线性油膜力的影响,得出了油膜厚度与油膜压力的关系,但是对于可倾瓦轴承其他因素的影响没有进行分析。Kyung-Bo Bang[7]等通过实验研究了传统六瓦可倾瓦轴承油膜温度与功率损耗之间的关系,通过改变可倾瓦轴承轴颈转速、轴承载荷和润滑油进口速度的大小,得出了这三者分别对轴承功率损耗的影响大小。但是,没能得给出其他可倾瓦功率损耗与轴瓦温度的关系。而对于线支撑的可倾瓦滑动轴承,汽轮机转子挠曲对油膜特性的影响不可忽视。因此,本文从汽轮机可倾瓦滑动轴承油膜狭小间隙内湍流流动角度,依据流体力学理论与数值计算方法,建立了可倾瓦轴承油膜湍流数学模型与油膜流场物理模型,运用ANSYS中CFX对可倾瓦滑动轴承油膜特性进行了数值模拟分析。
1 物理模型建立
1.1 转子挠曲的产生
随着火电厂大机组的发展趋势,汽轮机轴跨度逐渐增大,汽轮机轴会产生一定大小的挠曲变形,挠曲与载荷的关系如图1所示。

图1 挠曲与载荷的关系Fig.1 Relationship between deflection and load
挠曲变形对于瓦块点支撑的可倾瓦滑动轴承油膜特性影响较小,因为点支撑的瓦块在径向上可以自由调整。对于瓦块是线支撑的可倾瓦滑动轴承,其油膜特性势必会受到挠曲变化的影响。
设汽轮机轴在实际运行时的轴心线与理想中轴心线的夹角为θ。随着汽轮机载荷的变化,挠曲夹角θ也在不断变化,如图2所示。
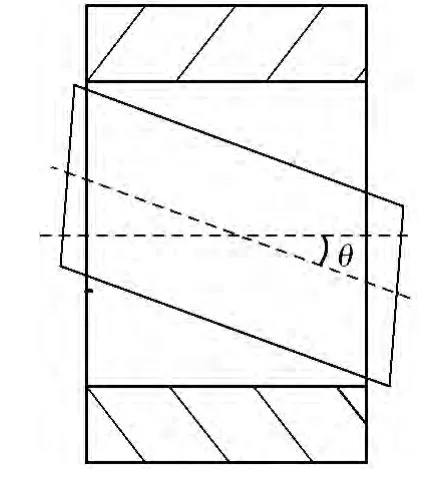
图2 挠曲夹角示意图Fig.2 Schematic diagram of deflection angle
在一般情况下,汽轮机轴的挠度和转角随截面位置的不同而改变,是坐标x的函数,即

式中:V为挠曲线方程;x为汽轮机轴长度,mm。
转角方程为

式中:θ为转角方程;θ为挠曲夹角,°。
式(1)和式(2)表示的函数关系分别称为挠曲线方程和转角方程。
当汽轮机轴弯曲时,若不计剪力影响,横截面在变形以后仍保持平面,与挠曲线相正交,则横截面转角θ与该截面处挠曲线的倾角相等,在小变形下,倾角θ很小,故有

式中:θ为挠曲夹角,°;V为挠曲线方程;x为汽轮机轴长度,mm。
由式(1)和(3)可知,挠曲线方程在任一截面x处的函数值,即为该截面的挠度。
1.2 模型的建立
可倾瓦轴承瓦块数量一般为3~10个或10个以上,最常见的结构是4个或5个。瓦块的布置方式有两种:载荷正对相邻瓦块支点之间和载荷正对某一瓦块支点,在受载荷最大瓦块的最小油膜厚度条件下,载荷对两支点之间轴承承载能力较高。可倾瓦轴承的瓦背材料为钢或铜铬合金,绝大多数瓦材料采用钢,其成本低、强度高。由于铜铬合金有较高的导热率,在较高转速的轴承中采用铜铬合金材料的瓦背,可以将工作热量由瓦面传递出去,避免瓦面温度过高而导致安全性降低。本文以载荷对着两支点之间的线支撑四瓦可倾瓦滑动轴承为例,根据表1的可倾瓦轴承设计参数,用Pro/E对四瓦可倾瓦滑动轴承油膜模型进行建模,其物理模型以及网格如图3所示。
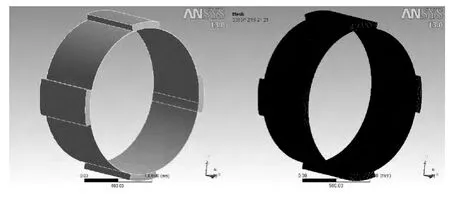
图3 四瓦可倾瓦滑动轴承油膜模型网格图Fig.3 Four pad tilting pad moving bearing oil film model and its grid graph

表1 可倾瓦轴承设计参数Tab 1 Design parameters of tilting pad bearing
2 物理模型的分析
2.1 控制方程
根据质量守恒定律,对于一个给定控制体的流体单元来说,将流入的流体质量减去流出的流体质量就得到了流体质量的增加率。根据流体单元流体质量的增加率,可以推导出粘性流体连续性方程:

式中:ρ为流体密度,kg/m3;t为时间,s;u、v、w为速度,m/s。
在流体单元中,假如润滑油的粘性力与温度变化无关,则不可压缩粘性流体的N-S方程为

式中:ρ为流体密度,kg/m3;ui为速度,m/s;t为时间,s;p为压强,Pa;μ为动力粘度,Pa·S;fi为单元质量流体所具有的质量力,N。
根据热力学第一定律的推导,润滑油运动的能量方程:

式中:ρ为流体密度,kg/m3;e为热力学能,J;▽为矢量微分算子;p为压强,MPa;T为热力学温度,K;k为傅里叶定律中传热系数,W/m2·K;Φ为耗散系数,表示粘性应力所作的功率。
2.2 数值求解
在ANSYS中,CFD提供了许多湍流模型,包括Spalart-Allmaras模型、k-ε模型、k-ω模型、雷诺应力模型(RSM)、大涡模拟模型(LES)。其中,Spalart-Allmaras模型是相对简单的方程模型,不能用于复杂的流场。雷诺应力模型(RSM)适用于雷诺应力明显具有各向异性的流场中,如龙卷风、燃烧室等带有强烈旋转的流场;大涡模拟模型(LES)适用于大涡结构受流场影响较大的流场中。
k-ω模型包含了流体的剪切流扩散,剪切应力输运k-ω模型简称SST(Shear Stress Transport)kω湍流模型,它是将k-ω模型和k-ε模型都乘以一个混合函数,然后再相加的结果。这种模型具有k-ω模型近壁区计算和k-ε模型远场计算两大优点。SSTk-ω模型增加了横向耗散导数项,考虑了湍流剪切应力,使用的湍流常数也和其他模型不同,应用范围更加广泛,可以用于带逆压梯度的流动计算,能够很合理的考虑流体的涡流黏度。
润滑油物性:润滑油密度为900 kg/m3,比热容cp=1885 J/kg·K,热传导系数k=0.4 W/m·K,动力粘度为0.02 Pa·s。设置换热类型为 Thermal Energy,湍流模型为SST模型。湍流密度选择默认的中等湍流密度,因为1% ~5%的湍流密度适合大多数流体。
润滑油边界条件的设置:进口为压力进口,压力值为0.2 MPa,进口润滑油温度为40℃;轴颈为旋转无滑移壁面,且是光滑的,轴颈旋转速度为3000 r/min;出口为开放出口,中等湍流密度,出口油温为55℃,因为在浸泡式可倾瓦轴承中,出口可认为是没有压力的。轴瓦为无滑移外壁,且是光滑的,求解器的收敛残差为0.0001。
3 模拟结果
当其他条件不变时,用ANSYS分别计算转角为0.02°、0.04°、0.06°、0.08°的四瓦可倾瓦滑动轴承油膜温度及油膜压力,如图4所示。
由图4a可以看出,对于整个油楔,汽轮机轴偏心处油膜较薄,油压峰值较高,轴颈另一侧油膜较厚,油膜极值压力较低。对于整周瓦块,每个瓦块都有一个油膜压力极值,极值大小不同。对于某个瓦块,沿着瓦块油膜分布的顺时针方向,油压从进口油压0.2 MPa逐渐升高达到极值,再逐渐降低至下一个进口油压0.2 MPa,而且瓦块支点处油膜分布不均。沿着瓦块宽度方向,油膜压力先增加至极值压力再逐渐减小,而且在极值压力附近油膜压的分布梯度变化较大。
沿着轴瓦的轴线方向,油膜压力逐渐增加到最大值后逐渐减小。当轴颈向轴瓦中心处偏移时,油膜压力极值中心向轴瓦支点处偏移,支点处的分界线逐渐明显,最终导致每块轴瓦上油膜压力极值区被分成两个压力区域(例如五瓦可倾瓦轴瓦上有两个正压力极值),油膜波动加剧,甚至出现负压区。
由图4b可以看出,随着挠曲转角增大,汽轮机可倾瓦滑动轴承油膜温度分布不均匀,油膜容易破裂,刚度变差,稳定性变差,不能很好的冷却轴瓦,从而引起轴瓦过热。
从图4c可以看出,当汽轮机转子挠曲逐渐增大时,对于线支撑轴瓦的四瓦可倾瓦滑动轴承来说,随着转角的增大,中轴面对称的油膜发生了变化,压力极值中心向轴内侧偏移,极值压力变化不大。但是转角大到一定程度时,油膜会破裂,不能很好地支撑轴颈的旋转,从而引起轴颈与轴瓦摩擦。
因此,对于可倾瓦四瓦轴承,线支撑轴瓦固然可用于重载汽轮机,但是其油膜特性易受轴的转角影响,此时可以使用点支撑轴瓦的可倾瓦滑动轴承,挠曲转角的大小对于使用点支撑瓦块的可倾瓦滑动轴承的轻载汽轮机影响较小。
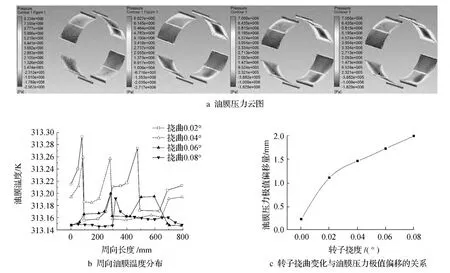
图4 四瓦可倾瓦轴承油膜特性图Fig.4 four watt tilting pad bearing oil film characteristics
4 结论
1)通过对轴瓦支撑为线支撑的可倾瓦滑动轴承油膜流场进行建模,选用SST湍流模型用于狭小间隙内的湍流流场,计算误差较小。
2)整个油楔每块轴瓦上均形成有油膜压力极值且油膜压力极值不同。当转子发生挠曲变化时,汽轮机轴偏心处油膜较薄,油压峰值较高,轴颈另一侧油膜较厚,油膜极值压力较低。
3)对于可倾瓦四瓦轴承,线支撑轴瓦固然可用于重载汽轮机,但是其油膜特性易受轴的转角影响,此时可以考虑使用点支撑轴瓦的可倾瓦滑动轴承。
[1]赵娟.高速滑动轴承-转子系统的动态特性研究[D].哈尔滨:哈尔滨工业大学,2009:1 5.ZHAO Juan.Research on dynamic characteristics of high-speed sliding bearing-rigid rotor[D].Harbin:Harbin Institute of Technology,2009:1 5.
[2] M.J.尼尔.摩擦学手册[M]:北京:机械工业出版社,2003(9):64 66.M.J.Nile.Manuel of tribology[M].Beijing:China Machine Press,2003(9):64 66.
[3]高庆水.基于CFD方法的液体动压滑动轴承动特性研究[J].润滑与密封,2008,33(9):65 67.GAO Qingshui.Research on dynamic characteristics of hydrodynamical journal bearing based on CFD analysis[J].Lubrication Engineering,2008,33(9):65 67.
[4]涂林,李多民,段滋华.基于Fluent的动压滑动轴承油膜力场模拟研究[J].润滑与密封,2011,36(4):82 86.TU Lin,LI Duomin,DUAN Zihua.Pressure field numerical simulation of hydrodynamic bearing based on Flunent[J].Lubrication Engineering,2011,36(4):82 86.
[5]张楚,杨建刚,郭瑞,等.基于两相流理论的滑动轴承流场计算分析[J].中国电机工程学报,2010,30(29):80 84.ZHANG Chu,YANG Jiangang,GUO Rui,et al.Simulation of journal bearing flow field using computational fluid dynamics two phase flow theory[J].Proceedings of CSEE,2010,30(29):80 84.
[6] MATTHEW CHA,PATRIK ISAKSSON,SERGEI GLAVATSKIH.Influence of Pad Compliance on Nonlinear Dynamic Characteristics of Tilting Dad Journal Bearings[J].Tribology International,2013,57(5):46 53.
[7] KYUNGBO BANG,JEONGHUN KIMA,YONGJOO CHO.Comparison of Power Loss and Pad Temperature for Leading Edge Groove Tilting Pad Journal Bearings and Conventional Tilting Pad Journal Bearings. Tribology International,2010,43(8):1287 1293.

