基于有限元的电力电缆过负荷运行能力研究
于 海,李 伟,王娜娜,张金桂
(1.东北电力大学电气工程学院,吉林 吉林 132012;2.齐鲁石化分公司热电厂,山东 淄博 255000;3.国网滨州供电公司,山东滨州256610)
电力电缆在电力系统中的使用日益普遍[1-2]。在电缆线路设计、规划及敷设中,电力电缆载流量是最重要的参数,确定载流量的方法有热路法[3]、边界元法[3]、有限容积法[4]、有限差分法[5-7]和有限元法[8-11]等。其中有限元法适用于各种工况,能够处理各种复杂边界,且计算精度高、速度快。为防止电缆事故对生产、生活造成巨大的经济损失,电缆运行载流量远低于额定载流量[12]。当电力系统输电线路发生故障或面临紧急供电需求时,电力部门往往采取停电检修、拉闸限电等措施,并没有充分发挥电力电缆裕量。本文基于有限元法,分析了电力电缆的过负荷运行能力,并给出了电缆过负荷运行能力曲线。
1 基于有限元的电缆温度场计算
1.1 温度场控制方程
交联聚乙烯电力电缆缆芯的最高允许温度为90℃,高于此温度,则会引起绝缘加速老化、降低电缆使用寿命[13]。电缆运行载流量不同,则电力电缆缆芯温度不同,因此电缆载流量的计算归结于电缆温度场的计算。
基于热传导定律和能量守恒原理,建立温度场控制方程,如图1所示。在单位时间内,对任何微元体传入微元体的热量和该微元体内部热源产生的热量之和等于该微元体所积蓄的热量。任意时刻正交各向异性物体内部的瞬态热传导微分方程为

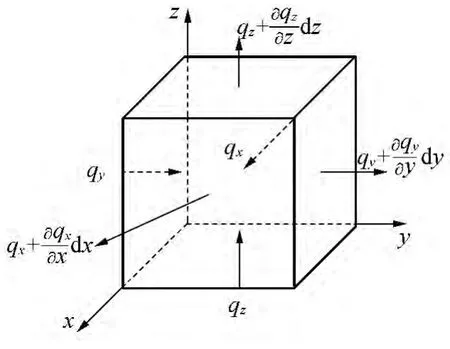
当物体温度达到稳态时,温度梯度为零,可得到稳态热传导微分方程为

式中:qx= -kx(∂T/∂x),qy= -ky(∂T/∂y),qz=-kz(∂T/∂z);kx、ky、kz为导热系数,W/(m·K);qb为微元体内部热源单位时间、单位体积所产生的热量;ρ为材料密度,kg/m3;c为材料的比热,J/(kg·K)。
1.2 初始条件和边界条件
对瞬态问题需要定义初始条件,即给出初始时刻物体的温度分布情况。
边界条件说明物体边界上热传递进行的特点,边界条件一般分为三种类型:第一类边界条件为温度边界条件,即任意点各个时刻温度是坐标和时间的已知函数;第二类边界条件为热流强度边界条件,即任意处各个时刻流入或流出物体表面的热流强度是坐标和时间的已知函数;第三类边界条件为对流边界条件和辐射边界条件。地埋电力电缆边界条件如图2所示。

1.3 温度场有限元的一般格式
温度场有限元的一般格式如下[14]:


式中:qb为内部热源;V为求解域的体积;c为比热;Sq为热流输入边界,q为边界上的热流强度;Sc为对流边界;h为对流系数;Sr为辐射边界;κ为等效辐射系数;Te为对流边界处的流体温度;Tr为辐射边界处的辐射源温度。
式(1)表示热流平衡原理,该式适用于电力电缆稳态温度场和暂态温度场计算。在很多情况下,寻找满足式(1)的温度函数比较困难。对于电力电缆温度场的求解,有限元法避免了寻找一个满足整个求解域的温度函数,即把求解域划分为几个有限单元,然后针对每个单元用节点上的温度建立该单元的温度插值函数。每个单元都有与其对应的温度场表达式,因此,可用所有单元的温度场函数代替满足整个求解域的温度函数。式(1)对整个求解域的积分可转化为对所有单元上的积分,在边界上的积分可转化为在相应单元相应边界上的积分。
1.4 电缆温度场损耗计算
电力电缆运行时,缆芯、绝缘层、金属护套等均会产生损耗,使电力电缆在运行中温度升高,当电缆产热与散热达到平衡时,缆芯温度为最高允许温度。由于金属护套通常采用交叉互联接地,有效减少了护套感应电压,使金属护套损耗降低。为简化计算,仅考虑缆芯损耗[3]:

式中:R0为20℃时缆芯单位长度直流电阻;θc为缆芯温度;ys为集肤效应系数;yp为临近效应系数;α20为20℃时缆芯电阻温度系数。
2 电力电缆有限元计算模型的验证
进行了220 kV电力电缆预埋温升试验。电缆预埋管埋深为1 m,土壤热阻系数为2.44 K·m·W-1,比热容[15]为 1277 J· kg-1·K-1,密度为1400 kg/m3,深层土壤温度为18℃。电缆参数如表1所示。
该试验持续153 h,通入电流1380 A,并使用热电偶元件测量缆芯、绝缘层、铝护套、外护层表面和预埋管表面温度。使用有限元程序计算电缆各层温度,计算温度与试验温度如图3所示。
从图3可以看到,缆芯的试验温度与计算温度最大相差4.29℃;外皮试验温度与计算温度最大相差为5.40℃;接近稳态时,缆芯的试验温度和计算温度仅相差1.14℃。由此证明了有限元计算的正确性。
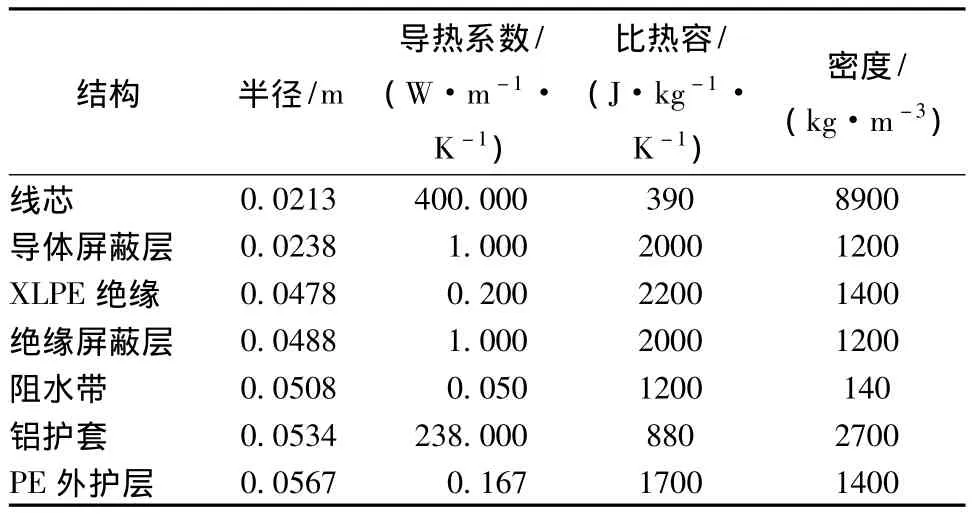
表1 220 kV 1000 mm2电力电缆参数Tab.1 220 kV 1000 mm2power cable parameters
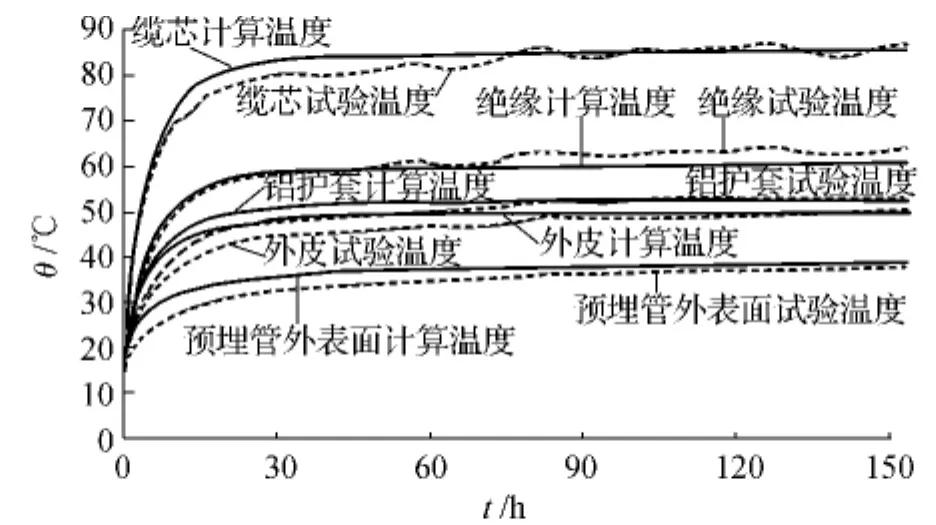
图3 220 kV预埋电缆恒定负荷下温升曲线Fig.3 Temperature rise curve 220 kV pre buried cables under constant load
3 电缆过负荷的运行能力
3.1 电缆运行载流量下的缆芯温升计算
电力系统在实际运行时,由于日负荷曲线具有显著的波动性,电力电缆运行载流量远远小于额定载流量。本文以东北地区春平甲乙线220 kV 1000 mm2电缆运行状况为例,计算过负荷运行能力。该电缆预埋敷设方式如图4所示,当环境初始温度为15℃、土壤热阻系数为1 K·m/W、土壤表面对流系数为12.5 W/(m2·K)时,使用有限元程序计算其额定载流量为957 A。春平甲乙线日负荷曲线如图5所示,其最大输送电流小于250 A,不足线路额定载流量的26%。
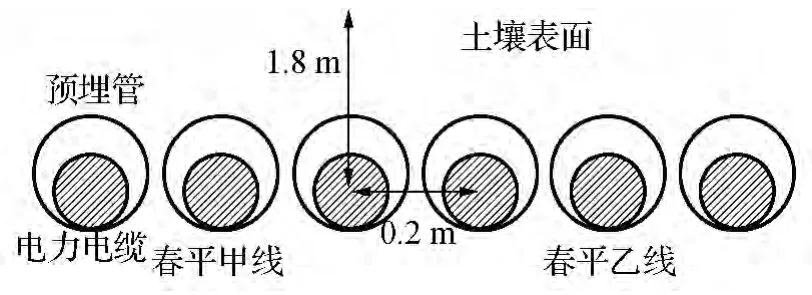
图4 春平甲乙线敷设方式Fig.4 Chun Ping A and B line laying mode
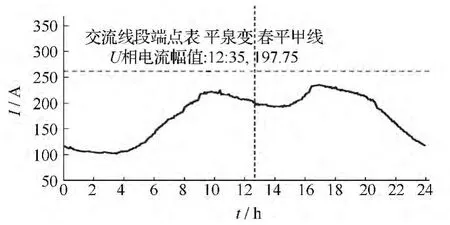
图5春平甲线日负荷曲线Fig.5 Chun Ping U line daily load curve
使用有限元程序计算得到甲线在日负荷曲线下的缆芯温升曲线如图6所示。从图6可以看到,缆芯的最高温度不足22℃,远低于缆芯温度上限90℃。所以,电缆使用容量远低于电缆的额定容量,电缆具有很大的过负荷运行能力。

图6 春平甲线12月2日缆芯温升曲线Fig.6 Temperature rise curve of cable core for Chun Ping A line in December 2nd
3.2 电缆过负荷运行能力计算
分别采用220 kV 2200 mm2与66 kV 1400 mm2XLPE绝缘电力电缆进行过负荷运行能力研究。电缆埋深1.8 m,环境初始温度为15℃,土壤热阻系数为1.0 K·m·W-1,初始负荷和过负荷分别用该电缆额定载流量的倍数(负荷标幺值)表示。电力电缆在不同初始负荷与过负荷下缆芯达到最高允许工作温度所需要的时间如图7、图8所示。

图7 220 kV电缆过负荷运行能力曲线Fig.7 220 kV cable over load capacity curve
由图7、图8可知:对于初始负荷为0.4倍额定载流量的220 kV 2200 mm2电力电缆,分别施加2.16、1.81、1.62、1.48 倍的过负荷时,经过 1、2、4、8 h缆芯温度达到了90℃;对于初始负荷为0.4倍额定载流量的66 kV 1400 mm2电力电缆,分别施加2.19、1.76、1.47、1.30 倍的过负荷时,经过 1、2、4、8 h缆芯温度达到了90℃。由于不同区域间电缆传输电能大小不同,且同等级电压下的电力电缆存在多种缆芯截面面积,本文又对初始负荷为0.4倍额定载流量的220 kV 400 mm2电力电缆进行了过负荷运行能力计算。当分别施加1.86、1.58、1.38、1.24倍的过负荷时,经过1、2、4、8 h缆芯温度能达到90℃。

图8 66 kV电缆过负荷运行能力曲线Fig.8 66 kV cable over load capacity curve
通过以上计算可知,由于过负荷运行能力采用额定载流量的倍数计算,当外界环境不变时,不同电缆过负荷运行能力基本相同。
4 结论
1)电缆预埋温升试验验证了有限元法计算电缆预埋温度场的正确性。
2)线路运行载流量不足额定载流量的26%,缆芯的最高温度不足22℃,电缆存在很大的过负荷运行能力。
3)当外界环境不变时,电缆初始负荷和过负荷采用负荷标幺值来计算,不同电缆过负荷运行能力基本相同。
[1]雷成华,刘刚,阮班义,等.根据导体温升特性实现高压单芯电缆动态增容的实验研究[J].高电压技术,2012,38(6):1397 1402.LEI Chenghua,LIU Gang,RUAN Banyi,et al.Experimental research of dynamic capacity based on conductor temperature rise characteristic of HV single-core cable[J].High Voltage Engineering,2012,38(6):1397 1402.
[2]刘刚,雷成华.提高单芯电缆短时负荷载流量的试验分析[J].高电压技术,2011,37(5):1288 1293.LIU Gang,LEI Chenghua.Experimental analysis on increasing temporary ampacity of single-core cable[J].High Voltage Engineering,2011,37(5):1288 1293.
[3]马国栋.电线电缆载流量[M].北京:中国电力出版社,2003.MA Guodong.Wire and cable ampacity[M].Beijing:China E-lectric Power Press,2003.
[4] 陶文铨.计算传热学的近代进展[M].北京:科学出版社,2001.TAO Wenquan.Advances in computational heat transfer[M].Beijing:Science Press,2001.
[5]郑良华,于建立,周晓虎,等.直埋电缆群载流量和稳态温度场计算新方法[J].高电压技术,2010,36(11):2833 2837.ZHENG Lianghua,YU Jianli,ZHOU Xiaohu,et al.New method to calculate ampacity and the steady-state temperature field of direct buried cable system [J].High Voltage Engineering,2010,36(11):2833 2837.
[6]曹惠玲,王增强,李雯靖,等.坐标组合法对直埋电缆与土壤界面温度场的数值计算[J].电工技术学报,2003,18(3):59 63.CAO Huiling,WANG Zengqiang,LI Wenjing,et al.Numerical computation of temperature distribution of underground cables and soil with combinatorial coordinates[J].Transactions of Electrotechnical Technology,2003,18(3):59 63.
[7] GAGGIDO C,OTERO A F,CIDRAS J.Theoretical model to calculate steady-state and transient ampacity and temperature in buried cables[J].IEEE Transactions on Power Delivery,2003,18(3):667 677.
[8]王有元,陈仁刚,陈伟根,等.有限元法计算地下电缆稳态温度场及其影响因素[J].高电压技术,2008,34(12):3086 3092.WANG Youyuan,CHEN Rengang,CHEN Weigen,et al.Application of finite element in calculation of underground cable steadystate temperature field and its influential factors[J].High Voltage Engineering,2008,34(12):3086 3092.
[9]梁永春,柴进爱,李彦明,等.基于FEM的直埋电缆载流量与外部环境关系的计算[J].电工电能新技术,2007,26(4):10 13.LIANG Yongchun,CHAI Jinai,LI Yanming,et al.Calculation of ampacity reduction factors for buried cables with surroundings based on FEM[J].Advanced Technology of Electrical Engineering and Energy,2007,26(4):10 13.
[10] ANDERS G J,CHAABAN M,BEDARD N.New approach to ampacity evaluation of cables in ducts using finite element technique[J].IEEE Transactions on Power Delivery,1987,2(4):969 975.
[11]付永长,张文斌,陈涛,等.不规则排列电缆温度场及载流量计算[J].电网技术,2010,34(4):173 176.FU Yongchang,ZHANG Wenbin,CHEN Tao,et al.Calculation on temperature field and current-carrying capacity of irregular arranged cables[J].Power System Technology,2010,34(4):173 176.
[12]鲁志伟,于建立,郑良华,等.交联电缆集群敷设载流量的数值计算[J].高电压技术,2010,36(2):481 487.LU Zhiwei,YU Jianli,ZHENG Lianghua,et al.Numerical calculation of ampacity for XLPE cables in cluster laying[J].High Voltage Engineering,2010,36(2):481 487.
[13]高小庆,姜芸,罗俊华,等.XLPE电力电缆过负荷温升与早期损害机理的研究[J].高电压技术,1997,23(2):62 64.GAO Xiaoqing,JIANG Yun,LUO Junhua,et al.Research on XLPE cable over-load temperature rise and early-stage damage mechanism [J].High Voltage Engineering,1997,23(2):62 64.
[14]梁醒培.应用有限元分析[M].北京:清华大学出版社,2010.LIANG Xingpei.Applied finite element analysis[M].Beijing:Tsinghua University Press,2010.
[15] LI H J.Estimation of soil thermal parameters from surface temperature of underground cables and prediction of cable rating[J].IEE Proc.Gener.Transm.Distrib.,2005,152(6):849 854.

