基于BP网络预测的地埋电力电缆动态增容

王娜娜，于 海，刘同同，陈江源，敖 明

(1．东北电力大学 电气工程学院，吉林 吉林 132012;2．吉林省电力有限公司 电力科学研究院，长春 130021)

社会经济的发展拉动用电量的需求不断增长。但是为安全起见，通常电缆输送容量远小于其额定容量值，甚至不到20%，按最大负荷运行计算其利用率，也难以达到50%。敷设新电缆集群［1］耗费时间和空间，仅考虑现行电缆时发现:线路出现故障时，非故障线路有容量裕度［2］，可适量承担故障线路甩出的负荷。所以合理增加非故障线路的运行容量可以方便又经济地实现可靠供电。因此本文针对已敷设电缆，对增加其输送容量进行研究，用BP神经网络预测增加容量后电缆热状态［3］，建立电缆温升［4－8］神经网络预测模型，并通过插值得到从增容开始，缆芯经过多长时间到达最高允许温度(90℃)。设计的试验针对80%负荷(小于额定负荷)、满负荷、过20%负荷(大于额定负荷)3种情况，试验结果验证了模型的正确性。

1 模型理论分析

1．1 增容后电缆可安全运行的最大时间

电缆在实际容量下稳定运行，增容后必然经历从初始稳态温度上升到缆芯最高允许温度90℃的过程，所需要的时间定义为tΔ。电缆在增容后，运行时间小于其相应的tΔ。不同的电缆初始容量和增容量，将对应不同的tΔ。电缆缆芯温度若小于90℃，可安全运行。本文模型的最终目标是获得tΔ。

1．2 BP算法及BP神经网络预测模型

1．2．1 BP 算法

神经网络是由大量处理单元互相连接而成的网络。前馈型BP神经网络权值的调整规则采用向后传播学习算法。其三层结构的输入层、中间层(隐层)、输出层之间采用全连接。当一对学习样本提供给网络后，神经元的激活值从输入层经各中间层向输出层传播输出层的各神经元，获得网络的输入响应后，按照减少目标输出与实际值误差的方向逐层修正各连接权值。随着误差逆向传播与修正，网络对输入模式响应的正确率也不断上升，最终完成学习。

1．2．2 模型建立

设定额定载流量为IN;增容后值为Inew;初始运行负荷为IC;初始负荷到达稳态后温度为即初始实际运行负荷与额定容量的百分比作为网络输入变量I1，其值反映初始实际运行负荷的大小即增容后负荷值与额定容量百分比作为网络输入变量I1′，其值反映增容程度的大小。I1、I1′运行条件对应的缆芯状态由tc开始升温，其升温过程的数据组为W，目标是预测I2(I2可以等于I1)、I2′运行条件下的缆芯温升数据组W′。本文学习样本是历史数据，每一组学习数据包括I1和I1’运行条件下的缆芯温升数据组W，I2、I2′、I2和I2′运行条件下的缆芯温升数据组W′，即输入向量是上一组运行条件下的缆芯温升数据组及下一组缆芯温升运行条件，输出向量是下一组运行条件下的缆芯温升数据组。部分学习样本的运行条件如表1所示。

根据这样的学习过程建立起前一组与后一组的关系，即运行条件改变前后的关系。

1．3 插值计算以及matlab实现

采取插值和拟合最为常用。缆芯温升历史数据是以30 min为时间间隔测得的，因此温升预测结果中的时间变量同样是以30 min为步长。对于过负荷最终稳态温度超出90℃，而要获得刚好对应90℃时所对应的时间tΔ，本文采用了插值进行计算。分段Hermite插值是用一条曲线来逼近，最高次数可高于三次。电力电缆的温升曲线为多个指数函数的叠加，因此为获取特定温度对应的时间，选用了分段Hermite插值。另外考虑了一阶导数，相对来说此方法比直接线性插值要光滑。选用MATLAB进行编程，输出预测和插值结果，其程序流程如图1所示。

表1 学习部分样本运行条件Tab．1 Operation conditions of part learning sample

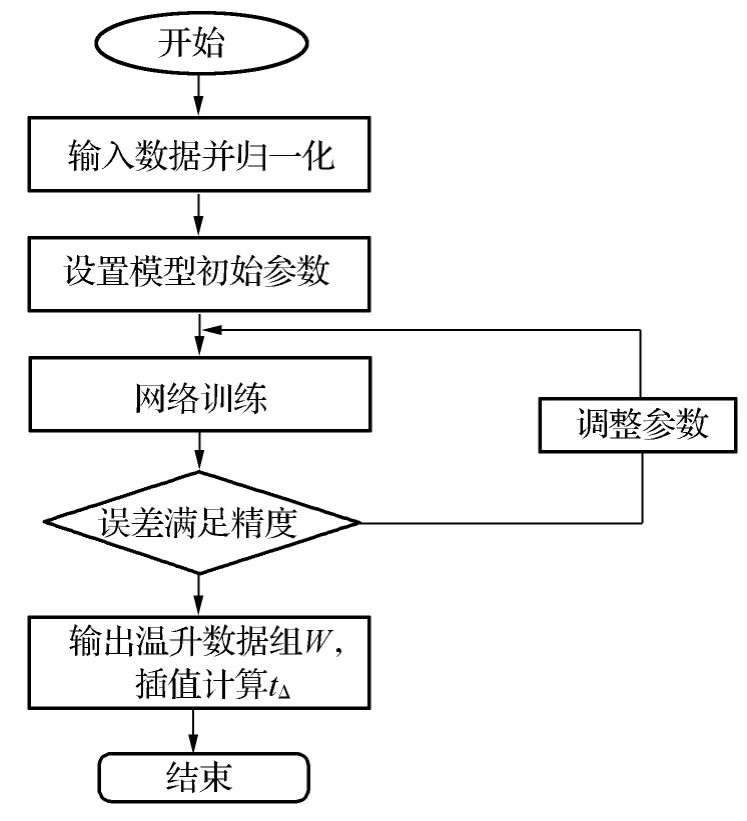
图1 matlab实现预测程序流程图Fig．1 Flow chart of using matlab realization farecast program

2 试验研究

2．1 试验的建立

为研究动态增容后电缆温升，校验所建模型，设计了66 kV电力电缆暂态温升试验。以66 kV直埋单芯交联聚乙烯电缆完成本次试验。试验接线原理图如图2所示。电缆埋深1．8 m，土壤热阻系数为1．25 K·m·W－1，密度为1400 kg·m－3，深层土壤温度为15℃。用热电偶监测电缆外皮、铝护套、缆芯及环境温度。

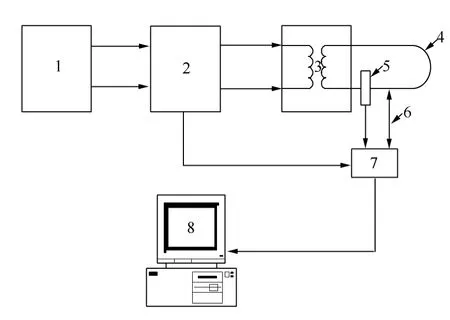
1—三相试验电源;2—单相调压器;3—大电流发生器;4—电缆回路;5—电流互感器;6—测温传感器;7—现场测量单元;8—上位机。

电流的施加方式如图3所示。试验电力电缆额定载流量IN为1700 A。以0～10 A(30%IN)阶跃电流作为电缆初始实际运行电流，到达稳态后电缆缆芯温度为21．6℃。增加额定容量至80%IN，即以510～1360 A阶跃电流作为模拟增容后运行电流;增加额定容量至满负荷，即以1360～1700 A阶跃电流作为模拟增容后运行电流;增加额定容量的120%，即以1700～2040 A阶跃电流作为模拟增容至过负荷运行电流。

2．2 试验结果与预测结果的对比分析

增容后的试验曲线和预测曲线如图4所示。增容50%时，电缆负荷由510 A跃变为1360 A，由预测结果得到缆芯温升至56．36℃到达稳态，即增容至80%IN，电缆缆芯温度小于最高允许温度90℃，tΔ理论上趋于无穷。试验结果与预测结果相符合，导体温升过程中预测温度与试验温度最大误差为4．6℃。增容后容量不超出额定容量，电缆可持续安全供电，无需考虑其缆芯状态。

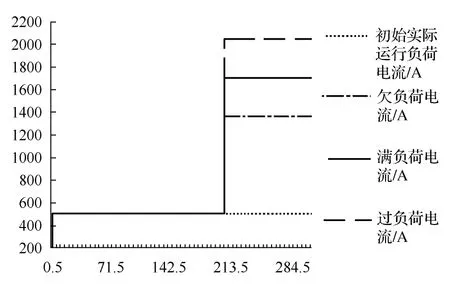
图3 电缆导体温升试验电流施加方式Fig．3 Current loading method of cable transient temperature rising test

图4 电缆缆芯温升试验值与计算值曲线Fig．4 Curve of cable core temperature rising test and calculation value

增容至满负荷时，电缆负荷由1360 A跃变为1700 A，由预测结果得到温升至81．5℃到达稳态，即满负荷时电缆缆芯温度小于电缆设计满负荷时最高允许温度90℃，约为额定工作温度的90．5%，tΔ理论上趋于无穷。试验结果与预测结果相符合，即地埋电缆由欠负荷增至满负荷时缆芯温度不会超出额定工作温度，可长时间运行。根据供电的需求，增容后容量小于等于额定容量，均可长时间运行，对电网供电。

增容至 120%IN(过负荷)时，电缆负荷由1700 A跃变为2040 A，由预测结果得到温升至101．48℃到达稳态，可以看出电缆的最高温度超出电缆设计满负荷时最高允许温度(90℃)10%以上，经插值计算tΔ为19．35 h。试验结果在图4中示出，到达稳态后温度试验值为100．47℃。温度最大误差3.94℃，试验tΔ约为23 h，与计算值基本一致。即地埋电缆增容至过负荷时缆芯温度将超出额定工作温度，但可以超负荷运行tΔ=23 h。

3 结论

1)地埋电缆初始实际运行负荷未达到额定值时，可以通过动态增容使其利用率最大化。满负荷甚至过负荷运行，只要运行时间在相应tΔ内，电缆缆芯最高温度就达不到电缆设计满负荷时的最高允许温度90℃，可安全运行。

2)BP神经网络应用于电力电缆动态增容具有可行性和优越性，预测具有较高的精度，实现运算十分迅速，为电力电缆的运行和管理提供了新依据。

3)对于其他不同的电缆等级、敷设环境等，增容计算结果的差异性需要进一步研究。

［1］赵健康，雷清泉，王晓兵，等．复杂运行条件下交联电缆载流量研究［J］．高电压技术，2009，35(12):3123-3128．ZHAO Jiankang，LEI Qingquan，WANG Xiaobing，et al．Experimental research on ampacity of extruded power cable under complex operating condition［J］．High Voltage Eng，2009，35(12):3123-3128．

［2］汤毅，王晓兵，陈燕萍，等．10 kV三芯交联电缆载流量的试验研究［J］．高电压技术，2009，35(11):2807-2812．TANG Yi，WANG Xiaobing，CHEN Yanping，et al．Experimental research on the current rating of 10 kV three-core XLPE cables［J］．High Voltage Eng，2009，35(11):2807-2812．

［3］ MICHAEL R，GREGORY P．Thermal modeling of portable power cables［J］．IEEE Transactions on Industry on Applications，1997，33(1):72-79．

［4］琚亚平，张楚华．基于人工神经网络与遗传算法的风力机翼型优化设计方法［J］．中国电机工程学报，2009，29(20):106-111．JU Yaping，ZHANG Chuhua．Optional design method for wind turbine airfoil based on artificial neural network model and genetic algorithm［J］．Proceedings of the CSEE，2009，29(20):106-111．

［5］雷成华，刘刚，李钦豪．BP神经网络用于单芯电缆导体温度的动态计算［J］．高电压技术，2011，37(1):184-189．LEI Chenghua，LIU Gang，LI Qinhao．The BP neural network used for dynamic calculation of single core cable conductor temperature［J］．High Voltage Eng，2011，37(21):184-189．

［6］刘刚，雷成华，刘毅刚．根据电缆表面温度推算导体温度的热路简化模型暂态误差分析［J］．电网技术，2011，35(4):212-217．LIU Gang，LEI Chenghua，LIU Yigang．Analysis on transient error of simplified thermal circuit model for calculating conductor temperature by cable surface temperature［J］．Power System Technology，2011，35(4):212-217

［7］雷鸣，刘刚，邱景生，等．单芯电缆线芯温度的非线性有限元法实时计算［J］．电网技术，2011，35(11):163-168．LEI Ming，LIU Gang，QIU Jingsheng，et al．Real-time core temperature calculation of single-core cable by nonlinear finite element method［J］．Power System Technology，2011，35(11):163-168．

［8］张施令，彭宗仁，刘鹏，等．电热耦合模型应用于高压干式直流套管径向温度和电场分布计算［J］．中国电机工程学报，2013，33(22):191-200．ZHANG Shi Ling，PENG Zongren，LIU Peng，et al．Electro-thermal coupling model for computation of radial temperature and electric field of resin impregnated paper high voltage direct current bushing［J］．Proceedings of the CSEE，2013，33(22):191-200．