弯折谱估计在抛物型方程模型电波传播中的应用研究
肖金光 周新力 刘晓娣
(海军航空工程学院电子信息工程系,山东 烟台264001)
引 言
抛物型方程(Parabolic Equation,PE)模型的分步傅里叶(Split Step Fourier Transform,SSFT)解法能够步进求解,且步长可灵活选取,适于计算远距离电波传播,受到了国内外的广泛关注[1-4].美国“高级折射效应预测系统”(Advanced Refractive Effects Prediction System,AREPS)的计算核心高级传播模型(Advanced Propagation Model,APM)就是基于PE研制的,类似软件还有对流层抛物方程程序(Tropospheric Electromagnetic Parabolic Equation Routine,TEMPER)[3,5].海上发生概率较高的蒸发波导中,电波频率和辐射角满足一定条件时可实现超视距传播,这种传播机制对低高度低仰角对海辐射源影响较大,具有重要的研究价值[6].在海风作用下,海面表面相对于可陷获传播波段的电波波长呈光滑或粗糙表面特性.PE通过边界阻抗引入下边界粗糙海面或者地形的影响,而边界阻抗取值依赖于电波在表面上的入射余角.常用的入射余角解法有射线追踪(Ray Tracing,RT)和平面波谱估计(Plane Wave Spectral Estimation,PWS)两种.APM和TEMPER在蒸发波导条件下采用RT[7],国内研究PE模型时,对入射余角延续了类似的思路[8].RT法所得入射余角在部分区域可能多值或无值造成入射余角取值震荡或不得不直接忽略表面粗糙的问题,而大气的超折射作用使得PWS的平面波前假设不成立,估计误差非常大[7,9].为了计算海杂波,2012年Ali Karimian等提出了弯折波谱估计(Curved Wave Spectral Estimation,CWS),通过将接收阵列的阵列流型与大气折射联系起来,克服了PWS对平面波前的要求,利用PE计算结果估计蒸发波导条件下的表面入射余角[10].但是,进行阻抗边界PE模型计算需要用到入射余角,对当前步进的PE结果进行入射余角估计,就会成了一个“鸡生蛋、蛋生鸡”问题.
为解决上述问题,本文提出单独运行一次在光滑平面条件下的PE,用CWS估计所需的入射余角,然后用于粗糙海面的PE计算,并通过数值试验验证了方法的可行性.
1 阻抗边界条件下的抛物方程模型
1.1 抛物方程模型
笛卡尔坐标系下,时谐因子为exp(-i wt),二维标量波方程忽略后向传播并作近轴近似,可得标准抛物方程(Standard Parabolic Equation,SPE)为[1]

式中:k为电磁波波数;n(x,z)为大气折射率;u(x,z)为场分量.考虑地球曲率的影响(re为地球半径),SPE的SSFT解为[11]

显然式(2)可以步进迭代解算,两指数项分别表征了传播媒质的折射效应和障碍物绕射效应.F、F-1为正、反傅里叶变换,变换点数N由奈奎斯特准则zmaxpmax=Nπ确定,zmax和pmax分别为需输出的高度和变换域最大值.若β是以辐射源点为顶点的最大计算域锥角,相邻两点高度差Δz需满足[1,11]

初始场由天线方向图的傅里叶逆变换求得,上边界采用Tukey窗函数滤波,在需要输出计算值区域上方添加吸收层,层内用窗函数滤波使场缓慢衰减为0,避免边界上的强反射“污染”计算域.下边界为光滑表面时,可由镜像原理将FFT进一步简化为正弦变换或余弦变换,但对于粗糙表面或地形等阻抗边界,需要引入满足SPE解的辅助函数

式中α为边界阻抗.根据Dirichlet边界条件,z=0时w=0,场分量为u的电磁波在阻抗边界上的传播就等效于为w在光滑阻抗边界上的传播,可得混合傅里叶变换(Mixed Fourier Transform,MFT)解.若引入式(4)的差分形式,同样可以步进求解PE,这种方法称为离散混合傅里叶变换(Discrete Mixed Fourier Transform,DMFT)法[8].
传播因子Fa定义为接收点场强E和自由空间接收点场强E0之比,由PE计算结果可求得[3]

则传输损耗L(x,z)为
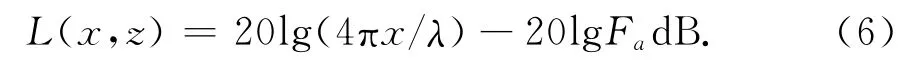
1.2 边界阻抗与入射余角
阻抗边界条件下,式(2)的求解与边界阻抗α密切相关.阻抗边界条件可描述为[8]
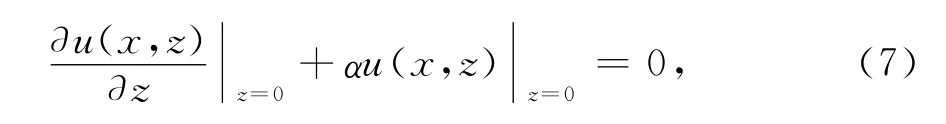
粗糙海面条件下有[8,12]

式中:Γ为电波在海面上的反射系数;θ为其入射余角;ρ为粗糙度衰减因子.若复介电常数为ξ′,则

式中:HPol和VPol分别表示水平极化和垂直极化.根据米勒-布朗模型,粗糙度衰减因子ρ为[13]

式中I0是第一类零阶修正贝塞尔函数.瑞利粗糙参数γ=2khrmssinθ,表示电波以入射余角θ入射到均方根高度为hrms的海面上时,入射波与反射波的相位差,由Philips海谱,风速为w时hrms=0.005 1 w2.γ趋于0时ρ趋于l,则光滑阻抗边界条件下α为
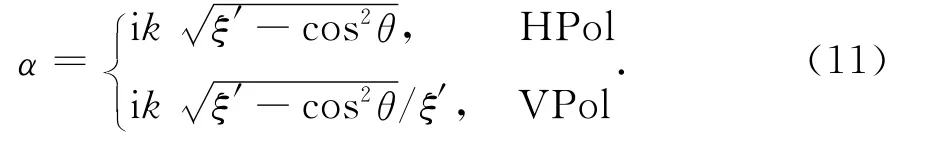
由于能够在蒸发波导中陷获传播的电波入射余角一般都小于1°,此时α又可以进一步近似为

由式(7)~(11)可知,α是θ的函数,因此入射余角θ对粗糙海面条件下的PE模型求解至关重要.
2 入射余角求解
2.1 RT和PWS谱估计法
RT本质上是几何光学近似,其泰勒级数近似解法较适于小仰角电波传播情况.根据折射率梯度将大气分层,计算射线轨迹[14],与电波的频率无关.
对大气折射率n引入平坦地球近似,以将电波沿地球表面的传播等效为水平传播,则平坦地球修正大气折射率为
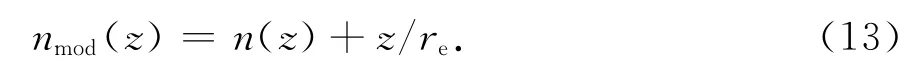
大气修正折射指数M为(nmod-1)×106.在蒸发波导中有[3]

式中:表面粗糙参数z0为1.5×10-4m;d为波导高度;M(z0)取为330M单位.取蒸发波导高度24m,天线高度20m,基于RT的射线轨迹如图1所示.
由图1可以看出:RT法用射线近似电波传播路径,在部分距离上没有射线到达表面,这种部分区域的无值现象在天线高度较高时比较明显,天线高度较低时会有所改善;而部分地方可能存在两个甚至多个值,这种多值性在天线高度较低时会更加突出.取24m高蒸发波导中天线高度为10m,RT估计的入射余角如图2所示.
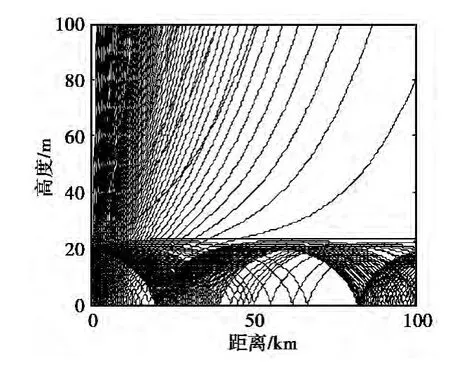
图1 20m天线的射线轨迹
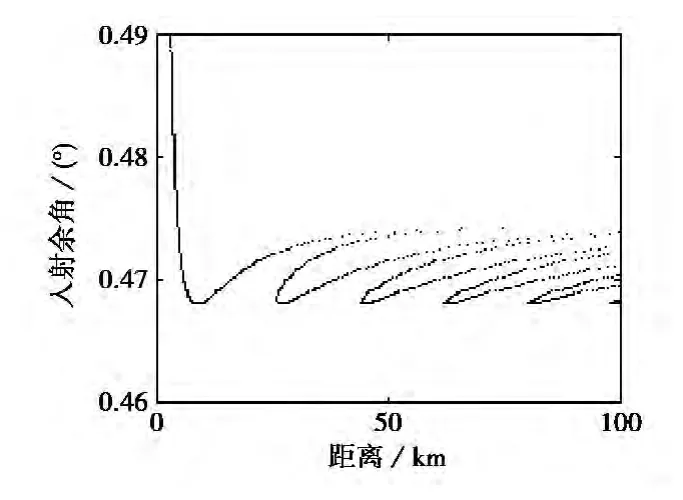
图2 10m天线RT估计的入射余角
由图2可知入射余角在部分距离上存在可能多值,这在天线安装位置较低时更加明显.这种在相邻区域甚至是同一距离上,因多条射线到达而形成的入射余角多值,恰恰表明了RT不能反映多路径传播电波的叠加效应,不能表征衍射、绕射机制,无射线到达区域的衍射、绕射和反射直接被忽略了.对于多值的取舍及造成取值震荡,文献[15]取RT估值最大值包络作为最终拟合值.
时域信号的频谱表示信号在频率上的能量分布,而空间谱表示的是信号在空间上的能量分布,从空间谱可得信号波达方向(Dirrect of Arrive,DOA).PWS假设电波具有平面波前,取空域上的部分场值(可以通过补零增加序列长度),经傅里叶变换后就是入射波的空间谱,搜索谱峰值即得到入射波主能量的DOA[16].APM中对于非蒸发波导情况下粗糙表面的DOA估计,通过单独运行一次光滑表面条件下的PE,取下表面附近的部分数据,估计到达下表面的电波的入射余角,另外在混合模式下,PE计算区域电波溢出方向的估计也采用PWS.但是蒸发波导条件下,大气超折射作用使得PWS的平面波前假设不成立,致使估计误差非常大.
2.2 CWS谱估计法[10]
高度z处的电波传播速度为

式中c0为真空电波传播速度.以θz入射到高度z处电波的波数为
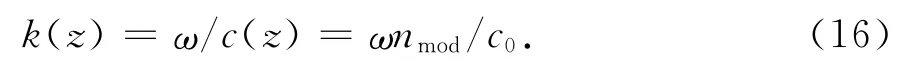
由费涅耳定理,水平波数为
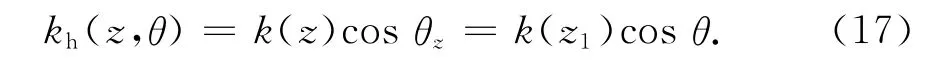
式中θ是海表面z1处的入射余角.则垂直波数为

垂直方向上场的相位变化就是垂直波数的积分.取贴近表面的Na点PE计算复场值进行谱估计,则第l点相对海面的相位差为
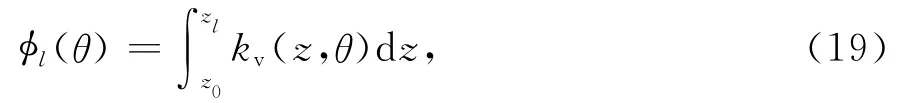
则空间谱为
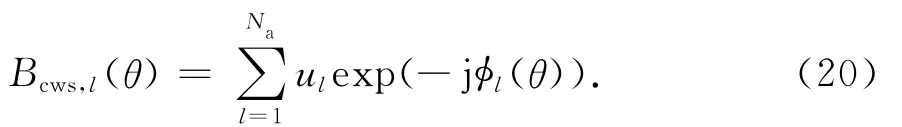
对于线性阵列,在-90°~90°范围内搜索式(18)的峰值,空间谱取得峰值时,对应角度θ即为入射波在参考高度上的入射余角,CWS通过式(12)~(18)将接收阵元相对参考高度的相位变化与大气折射率剖面和电波波长联系起来,从而可以应用于非平面波前的情况[10].而PWS实质上是CWS中垂直波数为常数的特例,第l点相对海面的相位差为

可得PWS空间谱为

由式(18)可知,CWS中,相同大气折射率条件下,电波频率越高,垂直波数越大,垂直接收阵列上场的相位变化越大,这一与电波波长相关联的特性是RT所不具备的.
2.3 三种方法估计特性比较
对RT、PWS、CWS三种入射余角方法的估计特性进行列表比较,如表1所示.
由表1可知CWS不仅表征了大气非均匀特性,而且与电波波长有关,估值具有唯一性,规避了RT和PWS的缺陷,因此用于海面电波传播的入射余角估计更具优势.

表1 RT、PWS、CWS估计特性比较
3 CWS用于PE计算
能否在一次计算中直接应用CWS呢?如果采用文献[10]的思路,直接对PE结果进行入射余角估计,就会在计算当前距离场值时需要基于该场值计算结果估计的参数,这显然是一个“鸡生蛋、蛋生鸡”的悖论.
针对这一矛盾,本文提出单独运行一次在光滑平面条件下的PE,用CWS估计所需距离上的入射余角,然后用于粗糙海面的PE计算,步骤如下:
1)PE模型相关参数设置;
2)根据波导剖面,用CWS估计各阵元相对于参考高度的相位差;
3)运行光滑表面条件下的PE模型;
4)根据3)的结果,用2)所得阵列流型,搜索谱峰值,对应的角度就是电波在该距离处海表面上的入射余角;
5)基于所估计的入射余角进行粗糙海面的PE模型计算.
算法可行性分析:
1)TEMPER对存在地形的情况也是单独运行一次在光滑平面条件下的PE,以进行PWS,在地形处取RT和SE的最大值,因为大气超折射作用使得PWS的平面波前假设不成立,导致误差太大而无法将PWS应用于蒸发波导情况[7].而CWS实质上是通过阵列流型的相位补偿,将入射波等效为平面波了,因此从原理上具有可行性.
2)由于CWS对光滑表面的PE计算场值进行估计,因此可以估计任意距离上入射余角,且估计值具有唯一性,弥补了RT部分区域存在多值或无值的两个重要缺陷.
3)避免了计算当前距离场值时需要基于该场值计算结果估计的参数这一悖论.
4)光滑平面条件下的PE,不需要考虑有限边界阻抗的问题,且初始化参数设置与第3步相同.运行光滑海面条件下的PE,计算量相对于RT要大,如果存在地形情况,相对于TEMPER所采取的在RT和PWS两种方法所得结果做选择,因为省略了RT,计算量反而是少的.因而从计算量的角度上具有应用的可行性.
5)蒸发波导陷获传播电波的入射余角一般小于1°,因此在超视距传播区域的入射余角估计中可以将谱峰搜索的范围限定在一个较小的半空间角度内,如0~1°,可以进一步降低计算量.
4 数值试验分析
4.1 参数设置
设辐射源频率为10GHz,高斯天线高20m,仰角为0°,蒸发波导高24m,粗糙海面时取风速为5 m/s,需输出高度为0~100m.根据式(3)阵元间距为0.16m,需1 024点FFT,步长取为Δr=4π(Δz)2/λ即296.5m.阵元数选为[10]

式中θBW是第一零点波瓣宽度(rad),对应角度值取为0.17°,则阵元数为126.
4.2 基于光滑海面PE的CWS性能分析
由式(17)、(19)、(21)及设定的参数,取角度θ搜索范围中一点0.47°为例,PWS和CWS各阵元相对参考海面的相位差φl(0.47)如图3所示.

图3 PWS和CWS相对参考面的相位差
由图3可知,由于蒸发波导中的大气陷获折射作用,各阵元间的相位差不再均匀,垂直接收阵列的底部相位梯度大,而顶部梯度小,这与式(14)所示大气折射指数剖面曲线特性一致.CWS估计所用的阵元相位阵列表征了这一作用机制,是其相对于PWS的本质区别.
对光滑海面条件下的PE计算场值作PWS和CWS估计,并与RT所估计的入射余角作比较,如图4所示.

图4 光滑海面入射余角估计
由图4可知,CWS与RT的入射余角估计值走势吻合较好,CWS估值略小于RT,而PWS误差较大.而且非常明显的,RT法在开始阶段的入射余角估计值密集,但在40~80km范围内和末端估计值较为稀疏,这与图1射线到达的位置是一致的.与RT不同,PWS、CWS是对光滑表面PE计算场值进行估计,可以根据需要获得所需步进点上的估计值.
图4中角度估值的最大值与辐射源高度和PE步长有关,步长小、辐射源布设位置高时,就会较大,反之亦然.相应的,在谱峰搜索时,可以根据几何关系或者RT法进行粗略估算,将搜索范围限定在一个适当小的角度范围内.
光滑海面CWS(风速为0)、粗糙海面CWS(对风速为10m/s的计算结果进行CWS估计)与RT三种方法超视距部分的估计值均值随辐射源频率的变化如图5所示.
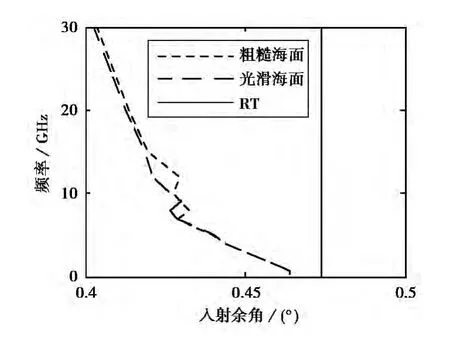
图5 估计均值与频率的关系
由图5可知,RT估值不随频率和风速变化,CWS估值比RT的估值小,电波频率越低,两者之间的差值越小,频率越高差值越大.由式(18)可知,频率越高,垂直波数受到大气非均匀特性影响越大,而RT与电波的频率没有关系.CWS通过使用场值进行角度估计,表征了多径信号在空间中的相互调制机制.比较光滑海面CWS(风速为0)、粗糙海面CWS(风速为10m/s)可知,风速越大,CWS估值越大,但总体上风速对CWS结果影响较小,这也是本文中用光滑海面PE结果代替粗糙海面PE结果(暂不可得)进行CWS估计的原因.
此外,CWS和RT估值均值随波导高度和天线高度的变化呈相同变化规律,在此不再赘述.
4.3 基于CWS的粗糙海面PE性能分析
基于光滑海面条件下PE模型计算结果,进行CWS估计,估计的入射余角用于粗糙海面条件下的PE模型计算.10GHz辐射源的电波传播损耗如图6所示(对于高于180dB的值和低于110dB的值均归入相近的区间表示).对不同频率的辐射源,分别基于RT法和CWS估计入射余角进行PE计算,在不同距离和高度上进行比较,分别如图7~9所示.为了清晰显示差异,图8、9中绘出了两者传播损耗的差值(CWS-RT).
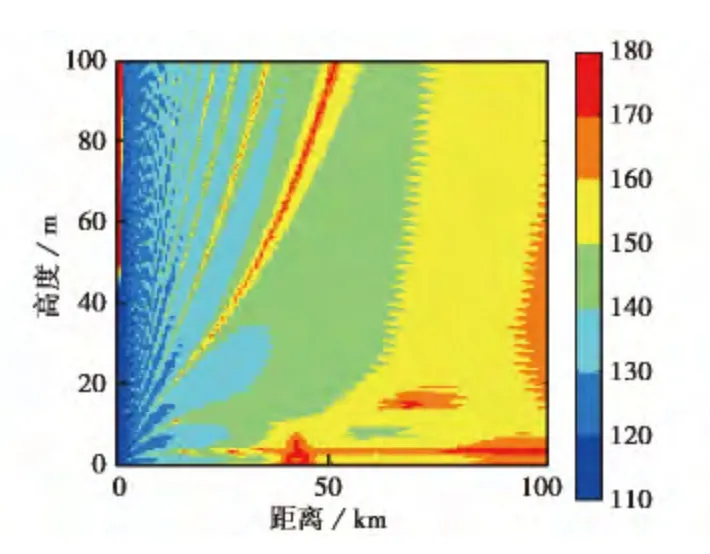
图6 基于CWS入射余角的电波传播损耗
由图7~9可知,10GHz信号源基于CWS的传播损耗比RT大0.1dB,走势一致(图7),而20 GHz时两者差值最大可达数dB(图8、9),且随距离增大而增大,在较低高度上比较明显.这与式(18)的内涵一致,较低频率电波的垂直波数变化较小,电波受大气非均匀特性的影响也较小,当频率变大,垂直波数变大,电波受大气非均匀特性的影响也变大.同样是表征大气非均匀特性,CWS与电波波长有关,而RT与电波波长无关.20GHz频率下,CWS的损耗总体上比RT的大,接收高度越高,差值曲线越趋于平缓;天线较低时低高度上的差值较大.这是因为天线高度较低时,RT估值存在多值性和跳跃性,不能表征多径信号叠加的缺陷更加明显.
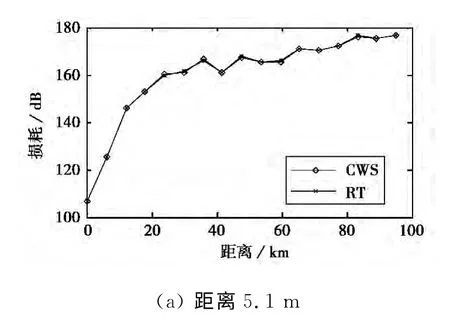

图7 20m高10GHz信号源的传播损耗

图8 20m高20GHz信号源的传播损耗
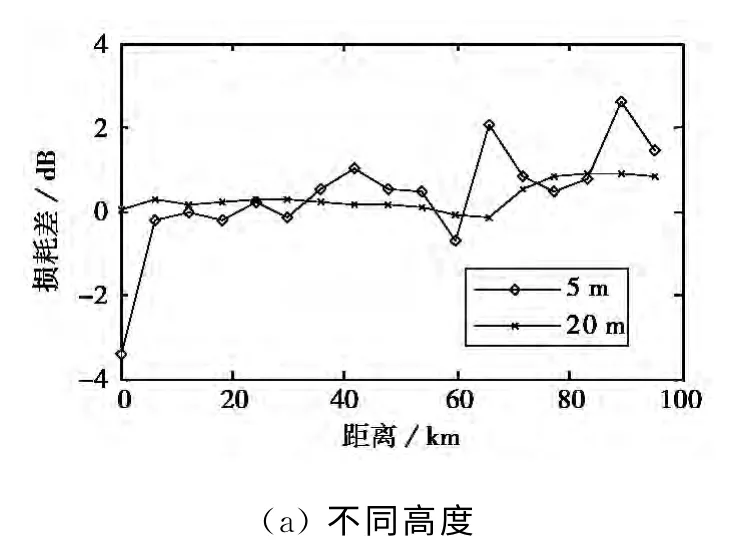
5 结 论

图9 5m高20GHz信号源的传播损耗
入射余角是抛物方程法求解阻抗边界电波传播中的重要参数.海面蒸发波导情况下,目前采用的RT法估计入射余角存在部分区域存在多值或无值以及与电波频率无关的缺陷,而PWS因为平面波前假设不成立而误差较大.CWS表征了大气非均匀特性对电波波前的影响,同时避免了计算当前值需要用到基于当前值的估计参数这一个悖论,本文提出了一种基于CWS入射余角估计进行PE模型海面电波传播计算的方法.通过对光滑海面的PE计算结果进行CWS谱估计,将估计的入射余角用于粗糙海面的PE模型计算,仿真和分析表明基于CWS的PE计算结果与基于RT的走势契合较好,较低频率电波的垂直波数变化较小,电波受到大气非均匀特性的影响也较小,两者差值较小;在较高频率时,CWS计算的低空传播损耗明显较大,更好地反映了海面低空大气超折射对较高频率电波的显著作用.新方法可以估计任意距离上入射余角,且估计值具有唯一性,规避了RT在部分区域多值或无值而相应造成的取值震荡,及其与电波频率无关的缺陷.新方法的计算量相比于纯RT法要大,相比地形条件下的RT和PWS选择法要小.新方法为蒸发波导和地形并存条件下,一致地求解粗糙面入射余角提供了解决方法,后续将予以研究.
[1]LEVY M F.Parabolic Equation Methods for Electromagnetic Wave Eropagation[M].London:IEE Press,2000:20-35.
[2]王红光,张 蕊,康士峰,等.大气波导传播的抛物方程模型研究综述[J].装备环境工程,2008,5(1):11-15.WANG Hongguang,ZHANG Rui,KANG Shifeng,et al.Overview on parabolic equation model research for atmospheric ducting propagation[J].Equipment Environmental Engineering,2008,5(1):11-15.(in Chinese)
[3]SIRKOVA I.Brief review on PE method application to propagation channel modeling in sea environment[J].Central European Journal of Engineering,2012,2(1):19-38.
[4]BARRIOS A E.Considerations in the development of the advanced propagation model(APM)for U.S.Navy applications[C]//Proceedings of the International Conference on Radar RADAR’2003Radar Conference,2003:77-82.
[5]BROOKNER E,CORNELY P R,LOK Y F.AREPS and TEMPER-getting familiar with these powerful propagation software tools[J].2007.
[6]黄小毛,张永刚,王 华,等.蒸发波导中电磁波异常传播特征研究及其应用[J].电子与信息学报,2006,28(8):1508-1512.HUANG Xiaomao,ZHANG Yonggang,WANG Hua,et al.A ray tracing algorithm for duct environment[J].Journal of Electronics &Information Technology,2006,28(8):1508-1512.(in Chinese)
[7]DOCKERY G D.An overview of recent advances for the TEMPER radar propagation model[J].IEEE Transactions on Antennas and Propagation,2007,44(1):896-905.
[8]郭立新,李宏强,杨 超,等.改进DMFT算法研究粗糙海上蒸发波导中的电波传输特性[J].电波科学学报,2009,24(3):414-421.GUO Lixin,LI Hongqiang,YANG Chao,et al.Characteristics of radio wave propagation in the evaporation duct environment over the rough surface by the improved DMFT algorithm[J].Chinese Journal of Radio Science,2009,24(3):414-421.(in Chinese)
[9]SPRAGUE R A,PATTERSON W L,BARRIOS A E.Advanced Propagation Model(APM)Version 2.1.04 Computer Software Configuration Item(CSCI)Cocuments[R].San Diego:Space and Naval Warfare Systems Command,2007.
[10]KARIMIAN A,YARDIM C,GERSTOFT P,et al.Multiple grazing angle sea clutter modeling[J].IEEE Transactions on Antennas and Propagation,2012,10(9):4408-4417.
[11]姚景顺,杨世兴.抛物方程模型在海上电波传播中的应用[J].电波科学学报,2009,24(3):493-497.YAO Jingshun,YANG Shixing.A terrain parabolic equation model for propagation over the ocean[J].Chinese Journal of Radio Science,2009,24(3):493-497.(in Chinese)
[12]刘爱国,察 豪.海上蒸发波导条件下电磁波传播损耗实验研究[J].电波科学学报,2008,23(6)1119-1203.LIU Aigou,CHA Hao.Experiment study of electromagnetic wave propagation Loss in oceanic evaporation duct[J].Chinese Journal of Radio Science,2008,23(6):1119-1203.(in Chinese)
[13]FREUND D E,WOODS N E.Forward radar propagation over a rough sea surface:an numerical assessment of the Miller-Brown approximation using a Horizonally polarized 3GHz line source[J].IEEE Trans on Antennas Propagat,2006,54(4):1292-1304.
[14]孙 方,王红光,康士峰,等.大气波导环境下的射线追踪算法[J].电波科学学报,2008,23(1):179-183.SUN Fang,WANG Hongguang,KANG Shifeng,et al.A ray tracing algorithm for duct environment[J].Chinese Journal of Radio Science,2008,23(1):179-183.(in Chinese)
[15]DOCKERY G D,KUTTLER J R.An improved impedance-boundary algorithm for Fourier split-step solutions of the parabolic wave equation[J].IEEE Transactions on Antennas and Propagation,1996,44(12):1592-1599.
[16]汤 俊.统计信号处理[M].北京:清华大学出版社,2006.

