基于博弈论的多基站协作波束成形*

任婵婵，张文娟，肖海林，李民政

(桂林电子科技大学信息与通信学院，广西 桂林 541004)

1 引言

多基站协作通信能够有效消除小区间的共信道干扰(CCI)，从而改善系统的频谱效率。文献［1］研究了在异构网络中基站协作的资源分配问题，使系统的传输速率得到极大的提高。文献［2］在上行系统中分析了真实信道条件下的协作可以显著提高抗干扰能力。文献［3］在基站协作MIMO蜂窝系统中，假设所有用户速率相等，通过不同基站协作通信得到传输功率下界，利用固有波束成形方案得到传输功率上界，进而得到容量界限。

波束成形作为多基站协作通信的关键技术，在已知信道状态信息(CSI)的情况下，能够有效地改善小区边缘用户的性能及公平性［4］。文献［5］联合利用预编码与波束成形算法消除小区间的干扰，所提算法虽然使用户的计算复杂度减小，但是也相应的降低了系统的性能。文献［6－7］均是在MISO系统下对协作波束成形算法进行研究。文献［6］在基站功率受限的情况下求得最优波束向量，同时也提高边缘用户的传输速率，但发射天线多于两根时，系统性能会大大下降。文献［7］研究了在传输速率中断概率给定的条件下，使系统效用函数最大化，但未考虑算法复杂度问题。文献［8］提出了基于对角化迫零波束成形算法，但算法本身也受天线数目的限制，且天线数量增多时其性能不能保证。

针对以上问题，本文提出了基于博弈论的波束成形算法，该算法的性能与天线数目无关，且计算复杂度也较小。此外，利用该算法不仅使小区效用达到最大，而且达到了抑制小区间干扰的目的。

2 系统模型

协作波束成形通信系统模型如图1所示，此模型为由N个小区组成的下行系统，每个基站有M根发射天线。每个小区内均匀分布着多个用户，为减少用户多天线尺寸问题造成信号相关性带来的系统复杂度，假设所有用户为单天线。为验证基于博弈论的波束成形算法干扰抑制的可行性和简化系统模型，不失一般性，每个小区选取一个边缘用户作为研究对象［9］。协作的基站通过骨干网连接到中央控制器，中央控制器负责处理共享的信道状态信息。

图1 协作波束成形通信系统模型Fig.1 Cooperative beamforming communication system model

假设基站i发送有用信号给本小区的边缘用户i，则第i个小区中的用户接收到的信号为

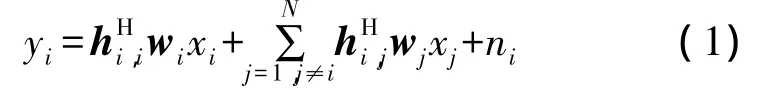
式中，第一项为有用信号，第二项为其他小区对第i个用户的干扰信号，ni表示均值为0、方差为σ2i的加性高斯白噪声(AWGN)，hi，j表示基站j到用户i的瑞利衰落系数，H表示共轭转置运算，wi表示基站i的波束向量，xi表示基站i的发射信号。

由于各个基站的CSI已经共享，可得用户i的信干噪比(SINR)为

式(2)中，波束向量wi应满足

其中，Pi表示基站i的发射功率，υi表示波束的方向向量。联合式(2)和式(3)，用户i接收的信干噪比还可以描述为

在已知用户信干噪比的条件下，可得用户i的速率为

以最大化用户速率为目标，优化问题可建模为

同时，各基站的发射功率与波束向量应满足

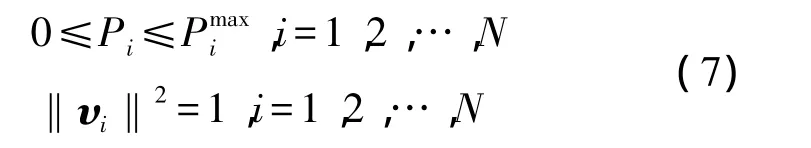
3 基于博弈论的波束成形算法

为优化多基站协作下的波束向量，首先，在式(5)的基础上建立波束成形的博弈论模型;其次，在纳什均衡存在且唯一的前提下，求得算法的纳什均衡。

3.1 博弈论算法

博弈论算法是满足个体最优的优化算法［10］。博弈论算法中包含3个要素:参与者集合、策略空间和效用函数。

(1)参与者集合

参与者包括所有的博弈方，由于假设所有的参与者均是理性的，所以各个博弈方均以获取最大利益为目标。设定各个小区为参与者，可得参与者集合为

(2)策略空间

博弈论的策略空间中包含每个参与者可供选择的策略集，参与者是同时选择策略的，即每一个参与者在选择策略时并不知道其他参与者的选择。以第i个基站发射的波束向量wi为具体策略，以Wi表示第i个基站参加策略的策略集，两者的关系可以表示为

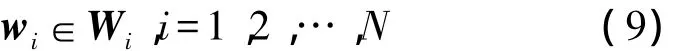
(3)效用函数

在博弈论算法中，效用函数是衡量性能好坏的依据，反应了参与者能够获得的利益。假设(w1，w2，…，wN)表示每个基站选定一个策略后形成的策略组合，则用ui(w1，w2，…，wN)表示所有基站选择策略(w1，w2，…，wN)时第 i个基站的效用。由于目标函数的优化方向与效用函数的增长方向是一致的，则效用函数可表示为

其中，uobj=lb(1+ri)，i=1，2，…，N 表示目标函数，uprice=μPi，i=1，2，…，N 为价格函数，表示基站要付出的代价，其中μ为常数。

综上所述，利用博弈论算法解决波束成形问题可建模如下:

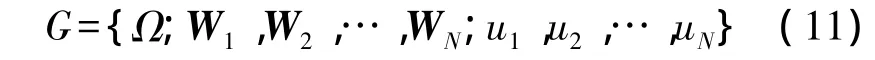
为了使目标函数最大化，需最大化效用函数，即

由于效用函数是关于基站的发射功率Pi的函数，对Pi求导可得

由式(14)可知，各个基站的可选策略应该是连续型的，则可以利用一定规则求得一个纳什均衡。纳什均衡是博弈论的一种解的形式，因此在求得纳什均衡之前，首先证明它的存在性与唯一性。

3.2 纳什均衡

定理1:在所提的博弈G中，波束成形算法一定存在纳什均衡。

证明:纳什均衡存在的充分必要条件为［11］:

(1)Pi是在欧式空间上的子集，且满足非空，有界闭集以及凸集;

(2)ui在P上连续，且在Pi处二次拟凹。

根据实际意义，Pi不可能为空，而且满足0≤Pi≤，所以Pi是有界的闭集。由于在欧式空间中，单点为一个凸集，所以Pi也是一个凸集。

因为拟凹函数与凸函数是等价的，所以只需证明ui是关于Pi的凸函数即可。在式(13)的基础上可得二阶导数为

由式(15)可知，效用函数ui在P上连续，在Pi处拟凹，故基于博弈论的波束成形算法存在纳什均衡。

定理2:若利用基于博弈论的波束成形算法得到最优效用函数的一个纳什均衡，则此纳什均衡是唯一的。

证明:纳什均衡唯一的充要条件是满足函数是标准函数［12］。标准函数在Pj≥0的情况下，应该同时满足正性、单调性及可延性3个条件。

(1)正性，即 g(Pj)＞0

当假设系统可行时，可知ui＞0，即满足lb(1+ri)＞μPi，则有 ΛPi=ri＞lb(1+ri)＞μPi，又已知 Pi＞0，所以。根据上文分析，c为大于1的常数，所以函数满足正性，即

(2)单调性，即假设 Pj≥P'j时，g(Pj)≥g(P'j)或g(Pj)≤g(P'j)

在 Pj≥P'j的假设下，可得 Λ(Pj)≤Λ(P'j)，判断函数g(Pj)的单调性，对其做差为

由式(17)可知，函数g(Pj)满足单调性。

(3)可延性，即对所有 α＞1，有 αg(Pj)＞g(αPj)

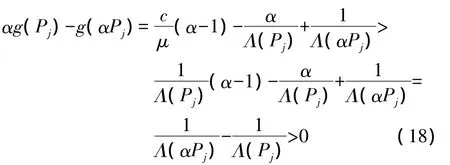
式(18)表示当 α＞1 时，满足 αg(Pj)＞g(αPj)，即函数具有可延性。

通过以上三点，证明了函数g(Pj)为标准函数，同时也说明算法存在唯一的纳什均衡。下面利用求解纳什均衡的方法求出此唯一解。

在博弈的过程中，一方参与者所选策略是由其他参与者上一时刻的策略决定的。在此博弈G中，若策略组合(w1，w2，…，wN)满足对每一个小区 i，是其他N－1个小区所选策略()的最优反应策略，此时就达到了各个小区不愿背离的平衡态，那么()就是所要求的纳什均衡，即

对所有集合Wi中的元素wi都成立，亦即是以下问题的解:

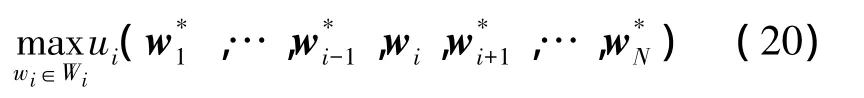
3.3 求解纳什均衡的步骤

(1)初始化。记 w=(w1，w2，…，wN)，取 k=0时刻，给出初始化策略组合w(0)=(w1(0)，w2(0)，…，wN(0));

(2)更新。记 w－i=(w1，…，wi－1，wi+1，…，wN)以最大化ui为目标，利用k时刻的策略组合w－i(k)更新小区i在k+1时刻的波束向量，得到新的策略组合w(k+1);

(3)判断。假设ε是一个很小的数，判断公式‖ui(k)－ui(k－1)‖＜ε是否满足，若不满足，则跳到步骤2;若满足，则最佳策略w*=w(k)。

4 仿真分析

首先给出波束方向图，在假设用户方向已知的情况下，验证算法的可行性;其次，给出效用函数的迭代过程，验证算法的收敛性。仿真中，基站的天线数M=4，每个用户配备单根天线，基站到用户的信道矩阵是均值为0、方差为1的复高斯随机变量，价格因子μ=0.4，波长是天线阵元间距的2倍，判决系数 ε 取值为10－7。

图2为3个基站协作时的波束方向图性能比较。其中，非协作算法指文献［13］中提到的波束向量选取方法，其波束向量为仿真中，设置本小区的用户方向为10°，相邻小区的干扰用户的方向分别为－150°、120°。从图中可以看出，相对于文献［13］中提到的非协作算法，所提出的基于博弈论的波束成形算法实现了在期望用户方向上得到较高的增益，在干扰用户方向上增益明显减小，体现出算法良好的性能。

图2 三基站协作时的波束方向图性能比较Fig.2 Beam pattern performance comparison of three base stations cooperation

图3为4个基站协作时的波束方向图性能比较。仿真中，同样的设置本小区的用户方向为10°，相邻小区的干扰用户的方向分别为－150°、－60°、120°。在与图2相同的约束下，由图3可知，当协作基站数目增大后，基于博弈论的波束成形算法仍可以使本小区的有用信号增强，使相邻小区的干扰信号减弱，达到了理想的效果，而非协作算法对所需抑制干扰的方向偏离更加严重。

图3 四基站协作时的波束方向图性能比较Fig.3 Beam pattern performance comparison of four base stations cooperation

图4给出了3个基站协作时3个小区效用函数的收敛曲线。设置期望用户方向为10°，干扰用户方向分别为－150°、120°。小区效用的每一步迭代均是相对于其他小区上一步策略的最优反应策略，从图中可以看出，3个小区的效用逐渐增大直至达到最大值，进一步验证了算法的收敛性。

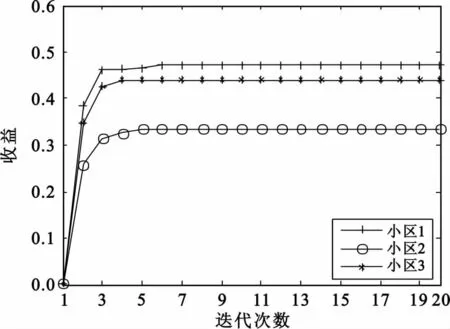
图4 不同小区的效用函数Fig.4 Utility function of different cells

5 结束语

波束成形技术是小区间干扰管理的一个关键技术，为最大化用户速率，本文提出了基于博弈论的波束成形算法，将此问题转化为求解纳什均衡的过程，并证明了纳什均衡的存在性和唯一性，最后求解出此纳什均衡。所提算法是一种使自身利益达到最大化的优化算法，故适用于个体最优化系统。仿真结果表明，在协作基站数目增多时，基于博弈论的波束成形算法仍然能够很好地减小相邻小区干扰用户的影响。此外，该算法具有很好的收敛性，在博弈的过程中，全部小区的效用均达到了相对最大值。在今后的工作中，将进一步研究此算法在其他场景中的应用。

［1］Li Q，Hu Q Y，Qian Y，et al.Intracell cooperation and resource allocation in a heterogeneous network with relays［J］.IEEE Transactions on Vehicular Technology，2013，62(4):1770－1784.

［2］Balachandran K，Kang J H，Karakayali K，et al.An analysis of uplink base station cooperation with practical constraints［J］.IEEE Transactions on Wireless Communications，2012，11(3):1056－1065.

［3］Wang P，Wang H，Li P，et al.On the capacity of MIMO cellular systems with base station cooperation［J］.IEEE Transactions on Wireless Communications，2011，10(11):3720－3731.

［4］Zhou T，Peng M，Wang W，et al.Low－ complexity coordinated beamforming for downlink multicell SDMA/OFDM systems［J］.IEEE Transactions on Vehicular Technology，2013，62(1):247－255.

［5］Hardjawana W，Vucetic B，Li Y H.Multi－user cooperative base station systems with joint precoding and beamforming［J］.IEEE Journal of Selected Topics in Signal Processing，2009，3(6):1079－1093.

［6］Liu Y F，Dai Y H，Luo Z Q.Coordinated beamforming for MISO interfereence channel:complexity analysis and efficient algorithms［J］.IEEE Transactions on Signal Processing，2011，59(3):1142－ 1157.

［7］Li W C，Chang T H，Lin C，et al.Coordinated beamforming for multiuser MISO interference channel under rate outage constraints［J］.IEEE Transactions on Signal Processing，2013，61(5):1087－1103.

［8］Kim H，Yu H，Sung Y，et al.An efficient algorithm for zero－forcing coordinated beamforming［J］.IEEE Communications Letters，2012，16(7):994－997.

［9］He S，Huang Y，Yang L，et al.A multi－cell beamforming design by uplink－downlink max－min SINR duality［J］.IEEE Transactions on Wireless Communications，2012，11(8):2858－2867.

［10］刘鹏，徐秀，巩思园，等.基于议价博弈论的无线协作中继网络性能改进算法［J］.电讯技术，2012，52(5):770－775.LIU Peng，XU Xiu，GONG Si－yuan，et al.Performance improvement algorithms based on bargaining game theory for wireless cooperative relay networks［J］.Telecommunication Engineering，2012，52(5):770－775.(in Chinese)

［11］Xu W Q，Wang X D.Pricing－based distributed downlink beamforming in multi－cell OFDMA networks［J］.IEEE Journal on Selected Areas in Communications，2012，30(9):1605－1613.

［12］Wang B，Han Z，Liu K J R.Distributed relay selection and power control for multiuser cooperative communication networks using stackelberg game［J］.IEEE Transactions on Mobile Computing，2009，8(7):975－990.

［13］Ramya B，Robert W Jr.Adaptive limited feedback for sum－rate maximizing beamforming in cooperative multicell systems［J］.IEEE Transactions on Signal Processing，2011，59(2):800－811.