基于联合概率加权的高分辨雷达目标点迹处理*
李思奇,陈怀新
(中国西南电子技术研究所,成都 610036)
1 引言
高分辨雷达[1]是采用宽带雷达技术,与窄带雷达相比可以获得更高的距离分辨率,因此在精确制导中得到了非常广泛的应用[2-3]。高分辨雷达通常工作在微波、毫米波频段,目标及部件的长度远大于波长,回波信号提供目标更多的特征信息,目标将占据多个距离分辨单元,可近似为一组离散的散射点,而这类目标被称为扩展目标。高分辨雷达在跟踪扩展目标时必须对目标的多散射点进行点迹数据处理,从而估计得到目标的散射中心。另外,雷达接收信号的同时不但含有来自目标的回波信号,也有从地物、云雨以及人为施放的箔条等物体散射产生的回波信号,这种回波信号称为杂波[4-5]。由于杂波往往比目标信号强得多,杂波的存在严重影响雷达对目标的跟踪能力,所以雷达目标点迹处理[6]需要考虑抑制杂波的方法,以提高在杂波区中跟踪目标的能力。
扩展目标经高分辨雷达信号检测[7-9]后在距离、角度上通常存在多个散射点,同时目标的散射点与虚假、干扰混在一起,成为了高分辨雷达目标点迹处理的难点。文献[10-11]中点迹处理方法的前提是认为信号检测出散射点都是目标的散射点,对其进行凝聚,这样会导致存在杂波干扰时点迹凝聚处理的精度下降。针对实际复杂环境,本方法采用目标点迹配对方法把多散射点数据进行归类,把目标产生的散射点归在一起,剔除脉冲压缩副瓣引起的虚假散射点和杂波干扰,再采用联合概率加权凝聚得到目标散射中心。这种方法可以有效抑制杂波的干扰,具有很好的可靠性,满足工程应用的要求。
2 目标点迹配对与凝聚方法
2.1 目标点迹配对
目标点迹配对就是为区别距离邻近而角度差别大或角度邻近而距离差别大的目标散射点,从而剔除异常的散射点,分辨和归并出目标散射点。对异常散射点的判别,结合卡尔曼滤波技术[12],利用目标点迹的前后时刻相关性判别。
首先,把雷达散射点实测的量测值距离、方位和俯仰(r,θ,φ),转换到直角坐标系下:
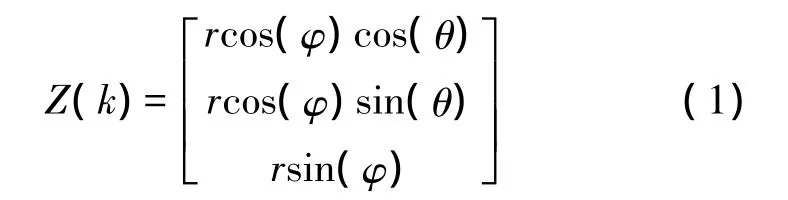
利用传感器观测方程预测当前时刻目标量测预测值:

其中,H(k)为观测矩阵,表达式如下:

本方法认为出现异常散射点表现为一种大新息,如果通过信号检测的散射点中出现异常值,新息必将增大。定义散射点残差(新息)变量的表达式为
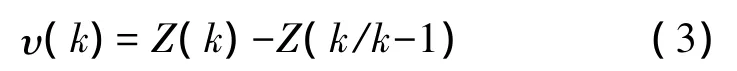
其中,υ(k)是均值为零的高斯随机向量,其协方差矩阵为
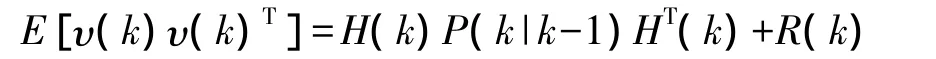
式中,P(k|k-1)为预测协方差矩阵,R(k)为量测噪声协方差矩阵。
利用上述计算出的散射点残差及其统计性质对散射点量测值Z(k)的每个分量进行判别,判别式为
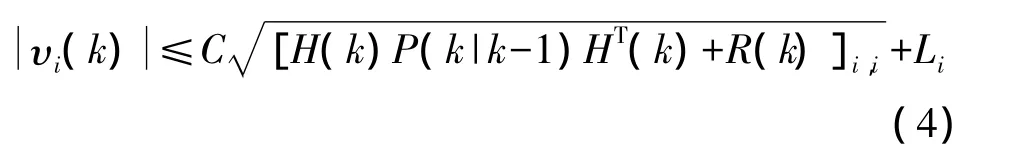
其中,下角i表示矩阵对角线上的第i个元素,υi(k)表示υ(k)的第i个分量,Li表示目标某一方向长度,HT表示矩阵H的转置;C为常数,可根据实际情况选取,通常可选3或4。如果散射点残差的每个分量都满足上述判别式,则此散射点为目标散射点;反之,则此散射点是由杂波或干扰引起的异常散射点,将其剔除。
从上述点迹配对算法过程可以看出,递推滤波中的残差对异常值的判别能力取决于预测精度,即E[υ(k)υ(k)T]的大小。预测精度越高,判别异常值的能力就越强。
2.2 基于联合概率加权的目标点迹凝聚
为了抑制距离波门内强杂波和干扰,本文采用一种基于联合概率加权的目标散射中心估计方法。这个方法的主要思想在于:考虑了点迹配对上的所有目标散射点,并根据大量的相关情况计算出各概率加权系数及所有强散射点的加权和,然后用它来凝聚得到目标散射中心。
在累积量测Zk={Z(j)}kj=1上建立位置条件概率βm(k):
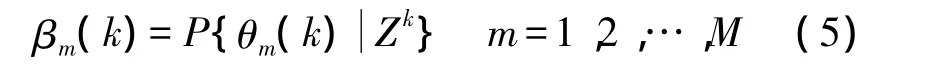
其中,M为经信号检测得到的散射点个数,事件θm(k)={散射点m为目标散射点},且这些事件是互斥、完备的,故满足

下面介绍βm(k)的计算方法。
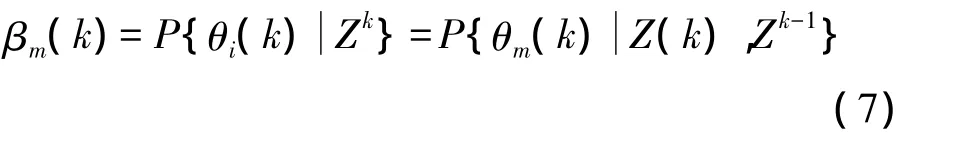
用贝叶斯原理,可以写成

其中,c是一个归一化常数,具体表达式如下:
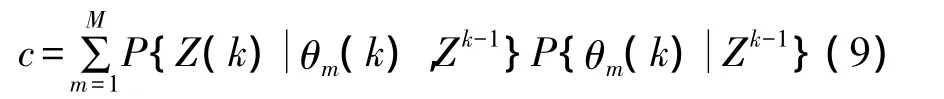

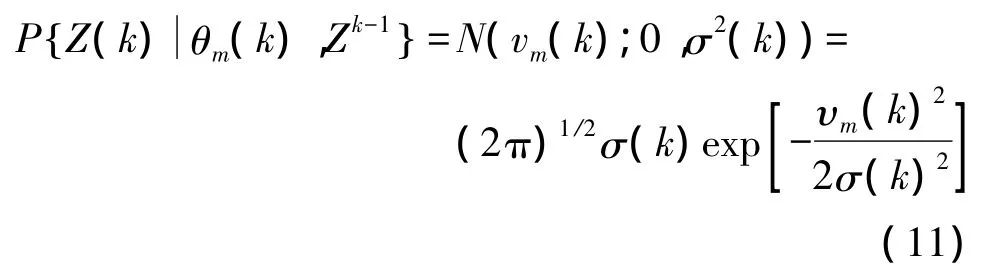
把散射点回波幅度代入上述得到的条件概率中,计算联合概率权值β'm:
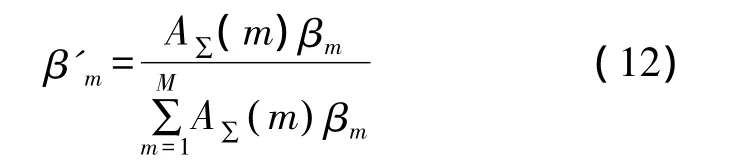
其中,A∑(m)为第m个散射点回波信号幅度。目标多散射点经上述计算的联合概率加权融合后,最终估计得到目标散射中心位置Z0(k):
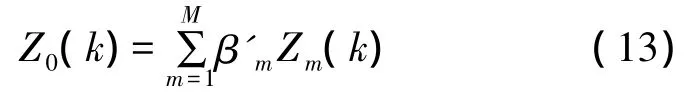
其中,Zm(k)为第m个散射点的量测值。
2.3 目标点迹数据处理步骤
以上对本算法原理进行了详细推导,这里归纳总结出目标点迹数据处理流程如图1所示,具体步骤如下:
(1)信号检测后的散射点Z(k),经式(3)计算出散射点残差υ(k);
(2)残差υ(k)由判别式(4)判断是否为异常值,如果是异常值,则概率,将其剔除,不参与散射中心估算;
(3)再把残差υ(k+1)代入式(8)计算位置概率权值βm(k);
(4)把散射点回波信号幅度 A∑(m)代入式(12)计算联合概率权值β'm(k);
(5)将概率β'i(k)代入式(13)得到目标散射中心的位置Z0(k)。
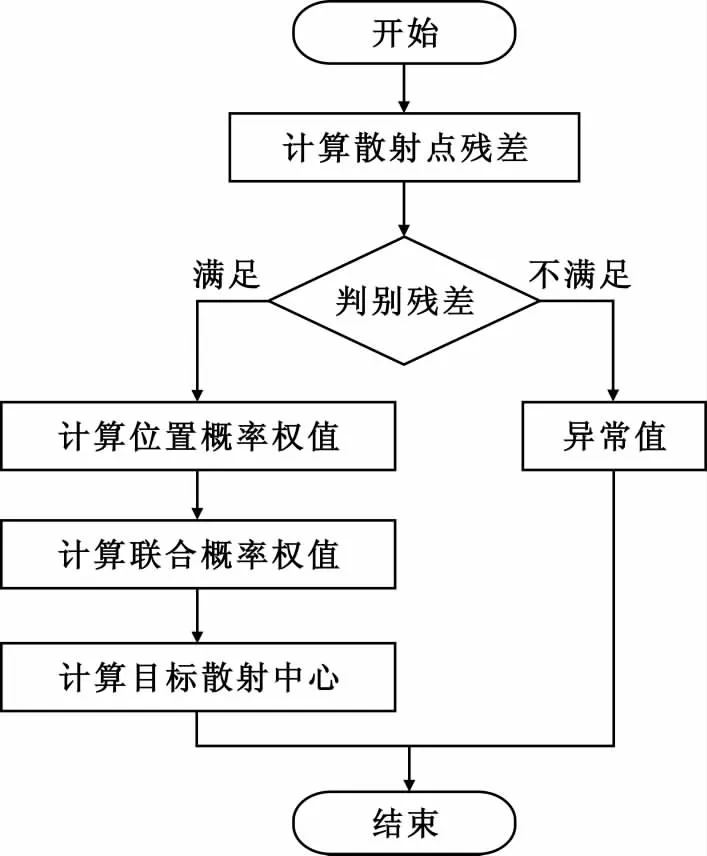
图1 目标点迹数据处理流程Fig.1 The process of target dot processing
3 仿真分析
仿真条件说明:假设目标尺寸15 m×10m,运动初始位置为(6600,5000,4800)m,运动轨迹的具体表达式如下:

雷达的观测位置(0,0,0)m,其发射频率35 GHz,线性调频带宽80MHz,脉冲重复间隔1 ms,需积累脉冲10个,即雷达观测的数据更新周期为10ms,信噪比为12 dB,杂波或干扰服从均匀分布。高分辨雷达的波长远远小于目标尺寸,即为扩展目标,同时目标多散射点均匀分布,分布参见图2所示,采用蒙特卡洛仿真统计基于质心算法的点迹处理方法和本方法的精度曲线及均方根误差。
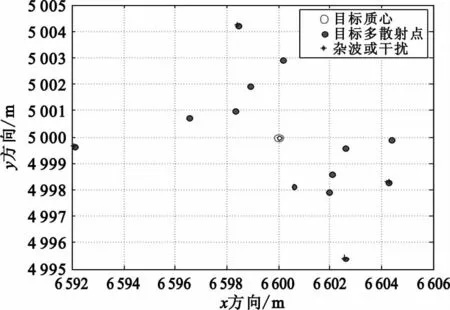
图2 在xy平面目标散射点及杂波分布Fig.2 Target scatter dot and clutter distribution in xy plane
软件仿真雷达在1 s内对目标连续观测,对比分析了质心算法和本算法的目标点迹处理结果。图3展示了在xy平面上目标点迹经配对和凝聚处理后散射中心估计曲线,从图中可以看出经本算法点迹处理后的散射中心曲线波动明显小于质心算法。

图3 在xy平面,目标点迹凝聚曲线比较Fig.3 Target dot clotting curve comparison in xy plane
图4~6分别表示雷达目标经点迹处理后距离、方位、俯仰精度曲线,从图中可以清晰看出本算法经点迹处理后距离、方位、俯仰误差水平低于质心算法。
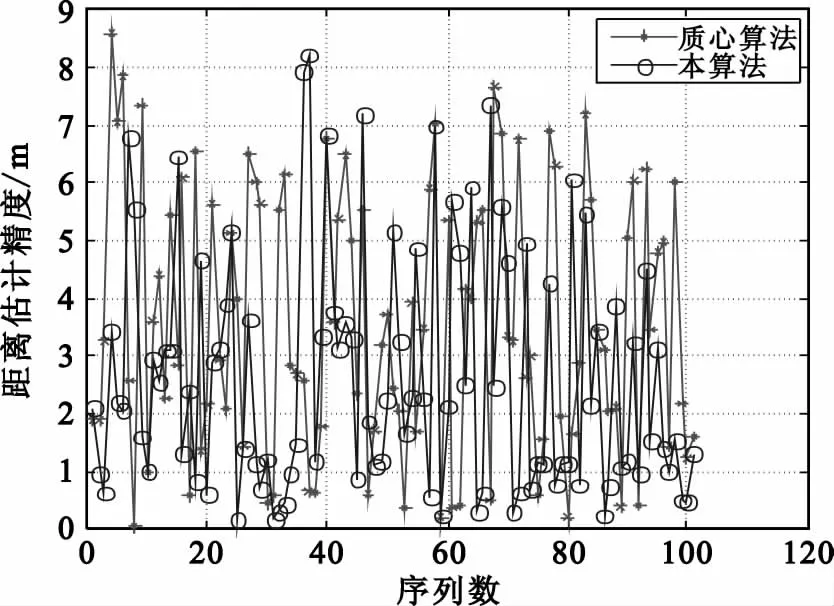
图4 距离精度曲线比较Fig.4 Range precision curve distribution
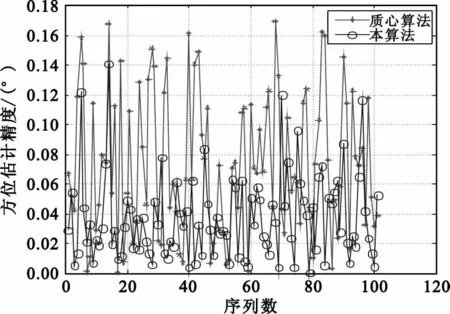
图5 方位精度曲线比较Fig.5 Azimuth precision curve distribution
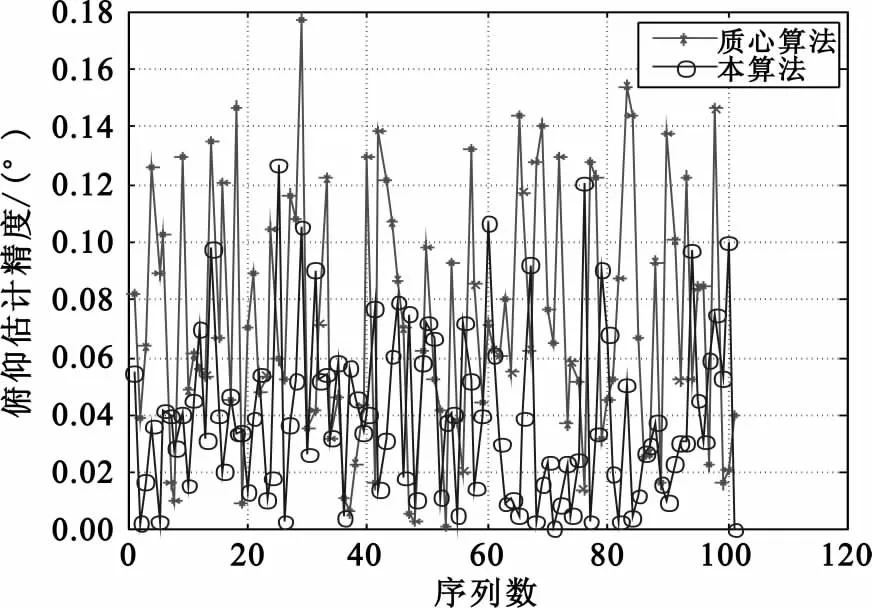
图6 俯仰精度曲线比较Fig.6 Pitch precision curve distribution
经50次蒙特卡洛仿真统计均方根误差(RMSE),如表1所示,可见本算法相比质心算法在距离、方位、俯仰精度上分别提升了20.63%、47.51%和41.03%,表明了本算法在抑制杂波或干扰的有效性,提高了目标散射中心估计的精度。
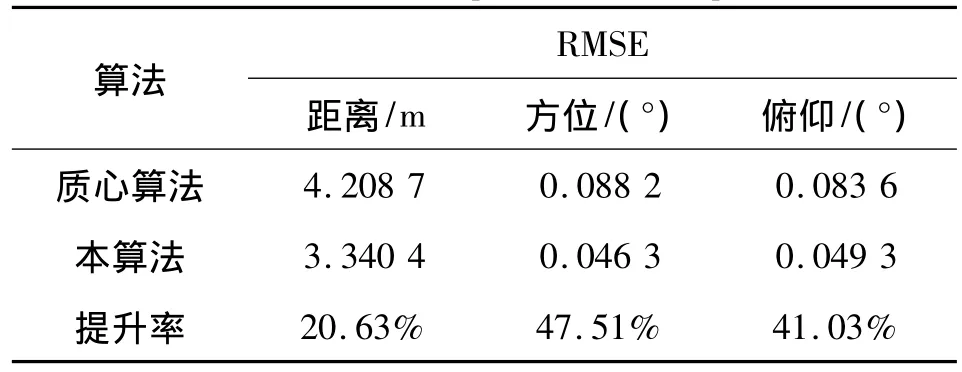
表1 均方根误差(RMSE)比较Table 1 Root mean squares error comparison
4 结论
本文针对高分辨雷达目标多散射点问题和杂波干扰的复杂环境,提出了一种高分辨雷达扩展目标点迹处理方法,详细推导了目标点迹配对归并多散射点数据,以及采用联合概率加权进行点迹凝聚处理的计算过程,并对算法进行软件仿真验证。仿真分析表明:本方法能有效抑制虚假散射点和杂波干扰,目标点迹凝聚精度在距离、方位和俯仰上分别提高了20.63%、47.51%和41.03%。本方法利用了历史时刻对当前时刻预测,所以要求预测过程可靠,如果预测精度越高,对异常值的判别能力就越强,抗干扰效果越好。
[1]Wehner D.High Resolution Radar[M].New York:Artech House,1987.
[2]王德纯,丁家会,程望东.精密跟踪测量雷达技术[M].北京:电子工业出版社,2007:72-82.WANG De-chun,DING Jia-hui,CHEN Wang-dong,Precision Tracking Radar Technology[M].Beijing:Publishing House of Electronics Industry,2007:72-82.(in Chinese)
[3]杨勇.毫米波雷达单脉冲跟踪系统仿真技术[J].电讯技术,2009,49(11):75-79.YANG Yong.Monopluse Tracking System Simulation Technique[J].Telecommunication Engineering,2009,49(11):75-79.(in Chinese)
[4]Billingsley J B,Farina A,Gini F,et al.Statistical Analyses of Measured Radar Ground Clutter Data[J].IEEE Transactions on Aerospace and Electronic Systems,1999,35(2):579-593.
[5]邢孟道,王彤,李真芳.雷达信号处理基础[M].北京:电子工业出版社.2010:40-84.XING Meng-dao,WANG Tong,LI Zhen-fang.Fundamentals of Radar Signal Process[M].Beijing:Publishing House of Electronics Industry,2010:40-84.(in Chinese)
[6]吴顺君,梅晓春.雷达信号处理和数据处理技术[M].北京:电子工业出版社,2010.WU Shun-jun,MEI Xiao-chun.Radar Signal Processing and Data Processing Technology[M].Beijing:Publishing House of Electronics Industry,2010.(in Chinese)
[7]Van Der Spek G A.Detection of a distributed target[J].IEEE Transactions on Aerospace and Electronic Systems,1971,AES-7(5):922-931.
[8]Conte E,Miao A D,Ricci G.CFAR Detection of Distributed Targets in Non-Gaussian Disturbance[J].IEEE Transactions on Aerospace,2002,38(2):612-621.
[9]Orlenko V M.Simulation of Target Detection Using a High Range Resolution Radar[C]//Proceedings of 2004 Second International Workshop Ultra Wide band and Ultra Short Impulse Signals.Sevastopol,Ukraine:IEEE,2004:121-123.
[10]简涛,徐向东,张莉,等.基于质量中心算法的两种点迹凝聚算法[J].空军雷达学院学报,2009,2(23)1:20-25.JIAN Tao,XU Xiang-dong,ZHANG Li,et al.Two Algorithms of Plot Centroid Based on Mass Center[J].Journal of Air Force Radar Academy,2009,2(23)1:20-25.(in Chinese)
[11]陈志坚.雷达数据处理中非真实目标点迹的处理[J].现代雷达,1995,17(3):43-48.CHEN Zhi-jian.The Processing for False Target Plots in Radar Data Processing[J].Modern Radar,1995,17(3):43-48.(in Chinese)
[12]蔡庆宇,张伯彦,曲洪权.相控阵雷达数据处理[M].北京:电子工业出版社,2011:3-4.CAI Qing-yu,ZHANG Bo-yan,QU Hong-quan.Phased-Array Radar Data Processing[M].Beijing:Publishing House of Electronics Industry,2011:3-4.(in Chinese)

