验前信息在导弹武器定型试验中的应用

魏太林

（解放军92941部队，辽宁 葫芦岛 125001）

验前信息在导弹武器定型试验中的应用

魏太林

（解放军92941部队，辽宁 葫芦岛 125001）

根据验前信息的获取、使用原则和分析计算方法，在某型导弹武器系统在定型试验中，通过实例计算出检验单发命中概率的检测方案，二项式分布Bayes假设检验方案。该方案在不同的验前概率下，制定了不同的接收和拒收标准。试验证明使用该方案可以节省试验弹数，提高检验置信度，降低军方风险。

验前信息、单发命中概率，置信度

引 言

海军导弹武器系统是海军现代海战中一类重要的武器装备，其中导弹的单发命中概率是导弹武器系统主要的作战指标，也是导弹武器系统定型试验中主要检验的指标之一。在战术技术性能试验考核时，重点考核了一般正常的性能参数，鉴于研制试验经费、周期、靶场试验条件等因素的制约，对于诸如远界（大射程）、近界（小射程）、高界（高高度）、近界（超低空）、大机动、大（小）航路、非主要杀伤区等边界条件试验考核相对较少，或者没有进行实弹射击考核，而是通过模拟仿真试验给出鉴定考核结论。对单发命中概率、命中精度、毁伤概率等战技指标的考核采用了小子样，甚至是极小子样方法，统计方法不规范，很难有较高的置信度。为了完成导弹武器系统的定型试验，使检验的战术技术性能指标具有较高的置信度，又要在规定的试验弹数量内进行检验评估，提高经济效益，解决试验中这样的突出问题，提出了利用验前信息的Bayes评估方法［1］。

1 验前信息

1.1 验前信息的获取

导弹飞行试验是武器系统指标验证的主要试验手段，其难点在于有限的试验子样下保证指标评估的置信度，验前信息的获取，一般有三种主要途径［2］，首先从历史资料中获取，其次依据理论分析或仿真结果中获取，再次凭籍经验的“主观概率”方法获取。在靶场试验工程中，使用验前信息可以达到以下目的：①在一定的试验精度或风险下，利用验前信息可以有效减少试验样本；②在一定的试验样本下，充分利用验前信息可以提高试验精度（置信度）或降低试验风险；③在一定的试验样本量和试验精度或试验风险下，验前信息可以改变检验的评定标准，使得原假设更容易被接收。

1.2 验前信息的使用原则

通过验前信息的收集、挖掘和加工，使它参加到统计推断中来，解决由于样本信息不足，导致统计推断可信度低的问题［3］，一般地，验前信息的使用应采取以下原则：

1.2.1 充分利用的原则

对于复杂大型武器系统的设计定型试验，验前信息是多种多样的。可能来自于不同试验阶段、不同试验项目和不同试验环境，大部分试验信息并非拿来直接应用的，必须进行必要的分析、处理和综合。因此，研究验前信息的分析、处理和综合方法是至关重要，是能够利用验前信息的基础。

1.2.2 保守的原则

验前信息的使用对试验方案、试验评定标准和试验结果都可能会有较大的影响。验前信息在使用过程中，不可避免会有人为因素，不当地使用验前信息，可能会造成试验评估结果和试验结论的“冒进”，因此，在验前信息的使用过程中必须谨慎，在验前信息的处理、综合过程中应尽可能“保守”一些。

1.2.3 有利的原则

有利的原则分为两方面内容：一是对试验方案制定有利于减少试验样本时才用。如较差的验前信息不但不会减少试验样本，反而可能会增加试验样本，这种情况下不用验前信息更为有利。二是验前信息的使用应有利于减小军方风险。一般情况下，采用验前信息后，军方风险可能小于研制方风险。由于利用验前信息是军方行为，因此，在计算使用方风险时，仍采用经典方法，而不计入验前信息。事实上，上述使用原则对军方是有利的，而对研制方并没有损失，这也是“保守原则”的具体体现。

1.3 验前概率的分析计算

（1）公式计算法

式中，λ=p1/p0，d=（1-p1）（1-p0）

该计算方法，一是验前概率的置信度无法估计，二是计算结果有“冒进”。为了改进这些缺陷，可采用蒙特卡洛随机模拟方法计算验前概率。

（2）蒙特卡洛随机模拟计算法［4］

设验前信息有导弹飞行试验样本n0，s0，导弹单发杀伤概率检验指标为p0。①进行n0次（0,1）之间的随机抽样，得到 X1，X2，…，Xn0；②对 X1，X2，…，Xn0从小到大进行排序，得到新的序列：X1，X2，…，Xs0，…，Xn0；③若Xs0≥p0，则计为导弹单发杀伤概率p0是“真”，否则计为导弹单发杀伤概率p0不为“真”；④重复 a）b）c）步 N 次（N≥20 000），统计 p0为“真”的次数为m；⑤计算p0是“真”的概率，即为验前概率π0

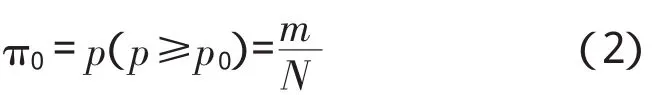
上述算法使得验前概率的π0的置信度为100%，因此，计算结果很保守。

1.3 验前概率置信度为的计算方法

在实际应用中，验前概率置信度γ取为检验与评估的置信水平相当，即为0.7～0.8之间。计算原理框图如图1所示。

2 某型导弹武器系统单发杀伤概率检验评估

对导弹单发命中概率检验，有二项分布经典假设检验方法和Bayes假设检验方法。评估采用二项分布 Bayes评估方法［5］。

2.1 经典假设检验方法

2.1.1 基本原理

当无验前数据时，可采用二项分布经典假设检验方法。对于统计假设：

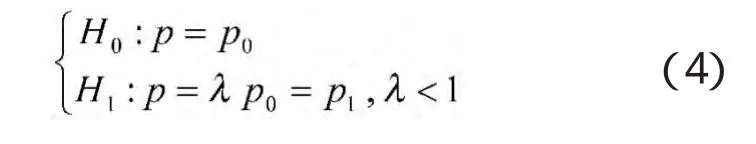
P0为单发命中概率设计指标；P1为使用方不希望但能接受的最低命中概率值［6］。检验决策为：

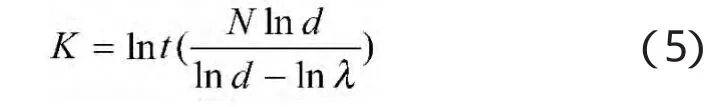
式中：d=（1-P1）（1-P0），λ=P1/P0。若 S≤K，拒绝H0；若 S＞K，接收 H0。式中，N 为试验发数，S 为接受H0的命中数。检验风险计算公式为：

式中：α为生产方风险；β为使用方风险。应用中要求双方风险相当并小于可接受值。

2.1.2 应用示例

若要求导弹命中数大于等于6发，按照二项分布经典假设检验，对单发命中概率P0=0.7和P0=0.75，计算符合条件要求的命中概率检验方案见表1。

表1 二项分布经典假设检验方案

从表1中可以看出，采用经典假设检验方案时，对于P0=0.7，当试验结果达到了9发6中；对于P0=0.75，达到了10发7中或8发6中，即可认为P0通过了检验，达到了指标要求。

2.2 Bayes假设检验方法

2.2.1 基本原理

当有验前数据时，可采用二项分布Bayes假设检验方法。对于统计假设：

当试验验前信息的试验成功数为S0，失败数为F0时，验前概率可由式（5）方法求得。则决策不等式为，接受 H1,否则接受 H0。

考虑了验前信息后犯两类错误的概率（Bayes风险）为［7］：

式中：α、β为经典风险，απ0为贝叶斯假设检验生产方风险；π1β为贝叶斯假设检验使用方风险；N为试验发数；Sn为试验成功数；Fn为失败数。

2.2.2 应用示例

对于单发命中概率P0=0.7，在不同的PH0之下，有Bayes检验方案见表2。从表2中可以看出，采用Bayes假设检验方案时，对于不同的验前信息，其检验的接收和拒收的标准有所不同。

表2 二项分布Bayes假设检验方案

3 结 论

验前信息在武器系统定型试验中的应用实例，是Bayes统计方法在靶场试验鉴定领域中的典型范例。通过在某型导弹武器系统定型试验中单发命中概率指标的检验，显示了验前信息方法在节省试验靶弹数，提高检验置信度，降低军方应用风险等方面的优势。该方法的应用无疑将在其他各型武器系统试验鉴定中得到广泛推广。

［1］曲宝忠，孙晓峰，李守秀，等.海军战术导弹试验与鉴定［M］.北京:国防工业出版社，2005.

［2］唐雪梅，张金槐，邵凤昌，等.武器装备小子样试验分析与评估［M］.北京:国防工业出版社，2001.

［3］武小悦，刘 琦.装备试验与评价［M］.北京:国防工业出版社，2008.

［4］张金槐，李菊生，常兆诚飞行器试验统计学［M］.长沙:国防科技大学出版社，1982.

［5］张金槐，唐雪梅.Bayes方法［M］.长沙:国防科技大学出版社，1989.

［6］吴 翊，李永乐，胡庆军.应用数理统计［M］.长沙:国防科技大学出版社，1995.

［7］王国玉，申绪涧，汪连栋.电子系统小子样试验理论方法［M］.北京:国防工业出版社，2003.

Application that Information Finalized the Design W hile Testing in theGuided M issileW eapon Before Testing

WEITai-lin
（Unit9294 of PLA，Huludao 125001，China）

Using priciple and analysing the computing technology of information according to testing,in some type guided missile weapon in is it in testing,is it examine system through instance single shot hitmeasuring scheme of probability to calculate out to finalize the design,the binomial is distributed Bayes and supposed the scheme of examining.Under this probability before different one is tested of scheme,have made different receiving and dishonouring the standard.The test proves that uses this scheme to save the test to play and count,improve and examine believing degree,reduce military's risk.

prior information，single-shotprobability，confidence

TJ760

A

1002-0640（2014）02-0178-03

2013-02-18

2013-03-21

魏太林（1962- ），山西沁源人，男，硕士，高级工程师。研究方向：武器系统。