解析函数的复合边值逆问题

武模忙，林峰，李锦成

（华侨大学 数学科学学院，福建 泉州362021）

文献［1-2］给出一类解析函数的Riemann边值逆问题的提法，讨论了该边值逆问题的正则型和非正则型情况的解法.文献［3］给出解析函数的Hilbert边值逆问题的提法，讨论了此边值逆问题的可解性，给出其可解条件和解的表达式.文献［4-5］给出了半平面中解析函数的Hilbert边值逆问题的提法，得到了该边值逆问题的可解条件和解的积分表达式.文献［6-8］分别研究了广义解析函数的Riemann边值问题、一类Dirichlet边值逆问题及半平面中的Dirichlet边值逆问题.文献［9-11］分别讨论了解析函数的非正则型Riemann Hilbert边值逆问题、解析函数在开口弧段上的Riemann边值逆问题，以及双解析函数在开口弧段上的Riemann边值逆问题.本文将讨论解析函数的复合边值逆问题.

1 问题的提法

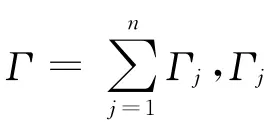
求函数组（Φ（z），Ψ1（τ），Ψ2（τ））.其中：Φ（z）为D中以Γ为跳跃曲线的分区全纯函数；Ψ1（τ）为Γ上的H类函数；Ψ2（τ）为L上的H类实函数 .满足下列边值条件，即

上述问题称为解析函数的复合边值逆问题，简称为RH-1问题，若G1（τ）≠0，G2（τ）≠0，λ（t）≠0，则称该逆问题为正则型RH-1问题，否则称为非正则型RH-1问题.以下讨论正则型RH-1问题.

2 问题的转化

由式（1）的第一式两端乘以g2（τ），并与式（1）的第二式两端乘以g1（τ）后相减，可得

由式（2）的第一式两端乘以r2（t），并与式（2）的第二式两端乘以r1（t）后相减，可得

这样，若求满足RH-1问题边值条件的分区全纯函数Φ（z），即求满足以下复合边值问题

3 问题的求解

3.1 Hilbert边值问题（9）的求解

考虑如下Riemann边值问题

Ⅰ）当K≥0时，Riemann边值问题（10在R0中有一个特解，即

式（12）中，Ω0＊（z）是Ω0（z）关于｜t｜＝1的对称扩张，则有（z）＝Ω（z），｜t｜＜1是Hilbert边值问题（9）的一个特解.因此，Hilbert边值问题（9）的一般解为

式（13）中，C0，C1，C2，…，C2K-1，C2K为任意常数，且须满足

Ⅱ）当K＜0时，当且仅当条件

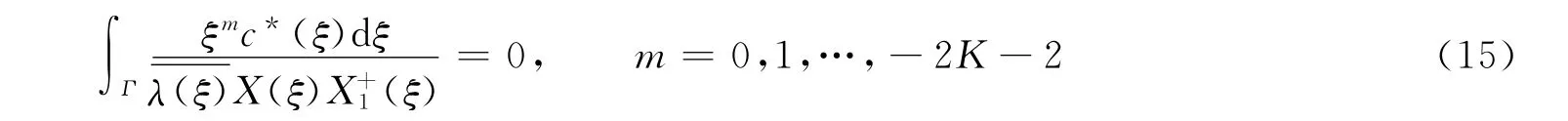
成立时，Hilbert边值问题（9）有唯一解为

因此，复合边值逆问题的解中Φ（z）的表达式为

式（17）中：当K≥0时，Φ0（z）由式（13）给出；当K＜0时，当且仅当条件式（15）满足，Φ0（z）由式（16）给出 .此外，Φ1（z），X（z）分别由式（7）和式（8）给出.

3.2 Ψ1（τ）的求解

将复合边值逆问题的解Φ（z）代入式（1）中，将其第一式两端乘以G2，2（τ）并与与第二式两端乘以G1，2（τ）后相减，可得

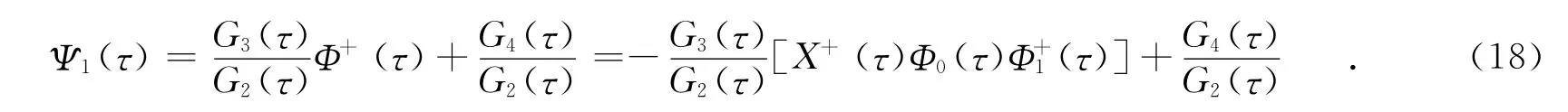
式（18）中，当K≥0时，Φ0（τ）由τ代入式（13）得到；当K＜0时，当且仅当条件式（15）满足时，Φ0（τ）由τ代入式（16）得到.由式（7），（8）及Cauchy型积分Plemelj公式，可以得到

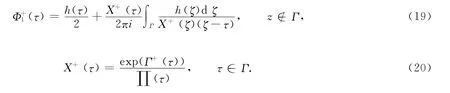
3.3 Ψ2（t）的求解

将复合边值逆问题的解Φ（z）代入式（2）中，两式相减可得

（Ⅰ）当K≥0时，由于有

式（24）中：I1为和式中第1，2项之和，I2为第3，4项之和，I3为第5，6项之和，I4为第7项.注意到有

式（36）中：I′1，I3，I4分别为式（35），（29），（30）给出.

定理1 对于正则型RH-1问题，当K≥0时，其一般解为（Φ（z），Ψ1（t），Ψ2（t）），其中Φ（z），Ψ1（τ），Ψ2（τ）分别由式（16），（17），（33）给出；而当K＜0时，当且仅当条件式（16）满足时，其有唯一解（Φ（z），Ψ1（t），Ψ2（t）），其中Φ（z），Ψ1（τ），Ψ2（τ）分别由式（16），（17），（36）给出.

［1］ 李星.一类 Riemann边值逆问题［J］.数学杂志，1996，16（3）：303-306.

［2］ 王明华.Riemann边值逆问题与奇异积分方程组［J］.数学杂志，1999，19（2）：175-180.

［3］ 王明华.一类 Riemann-Hilbert边值逆问题［J］.纯粹数学与应用数学，2006，28（2）：225-231.

［4］ 王明华.半平面中的 Hilbert边值逆问题［J］.四川师范大学学报：自然科学版，2011，34（2）：208-212.

［5］ 鄢盛勇.半平面中一类 Riemann-Hilbert边值逆问题［J］.贵州师范大学学报：自然科学版，2011，29（1）：52-57.

［6］ 王明华.广义解析函数的 Riemann边值逆问题［J］.宁夏大学学报：自然科学版，2006，27（1）：18-20.

［7］ 王明华.一类 Dirichlet边值逆问题［J］.系统科学与数学，2008，28（2）：225-231.

［8］ 王明华.半平面中的 Dirichlet边值逆问题［J］.四川师范大学学报：自然科学版，2006，29（6）：683-687.

［9］ 鄢盛勇.解析函数的非正则型 Riemann-Hilbert边值逆问题［J］.兰州理工大学学报，2011，37（2）：141-145.

［10］ YAN Sheng-yong.Inverse riemann boundary value problem along open arcs［J］.Journal of Yunan University of Nationalities：Natural Sciences Edition，2011，20（2）：107-112.

［11］ 鄢盛勇.双解析函数在开口弧段上的Riemann边值逆问题［J］.云南民族大学学报：自然科学版，2012，21（2）：125-129.

［12］ 路见可.解析函数边值问题教程［M］.武汉：武汉大学出版社，2009：97-102.