二阶线性系非振动的充要条件
陈敏,王晶海
(1.福建工程学院 数理系,福建 福州350118;
2.福州大学 数学与计算机科学学院,福建 福州350116)
1 预备知识
关于系统振动与非振动的研究很多[1-5],其中绝大部分是研究振动的,结论一般是振动的充分条件.本文给出非振动的充要条件及一个充分条件.考虑如下二阶周期系数线性系

定理A 或者式(2)的所有非零解都只有有限个零点,或者式(2)的所有解都有无穷多个零点[6].
定义1 若式(1)的所有非零解都只有有限个零点,那么称式(1)是非振动的.若式(1)的所有解都有无穷多个零点,那么称式(1)是振动的.
由于式(1)的非振动行可归结为式(2)的非振动性,所以文中只讨论式(2)的非振动性.
2 结论及其证明
定理B[6]式(2)非振动的充分且必要条件是对一切连续可微的π周期函数W(t)恒有
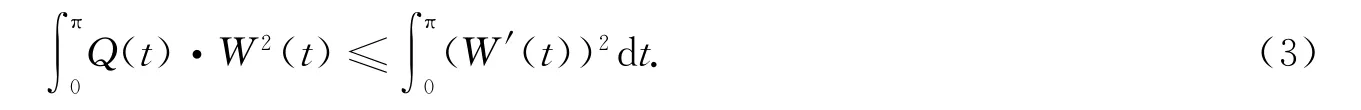

定理1 式(2)非振动的充分且必要条件是存在一个连续可微的π周期函数φ(t),使

证明 充分性 .设Q(t)≤φ′(t)-φ2(t),于是对任意连续可微的π周期函数W(t)有

必要性 .设式(2)非振动.由文献[6]可知式(2)存在一个非零解实解X(t)及一个正数ρ,使

式(4)中:ρ实为式(2)的特征乘数 .
可以肯定,对任意t∈R,X(t)≠0,若不然,可设X(t0)=0,那么,对任意自然数n有,X(t0+nπ)=ρn·X(t)=0,这与式(2)非振动矛盾.所以X(t)没有零点.
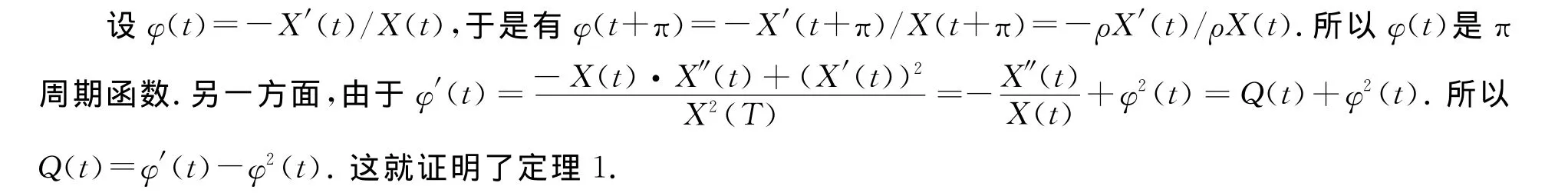
注1 若取ψ(t)=φ(t)+c,c>0常数且使2φ(t)-c<0,则易证Q(t)<ψ′(t)-ψ2(t).
3 实例验证

引理1 若式(3)非振动,且f(t)不恒等于0,则必有λ<0.
证明 由引理1可知,存在连续可微π周期函数φ(t),使


Mathieu方程x″+(λ-cos 2t)·x=0的最小特征值是λ0≈-0.122[7],由文献[6]可推断式(8)是振动的.由此可见定理1与定理2并非是粗糙结论.
例3 考虑二阶线性系

[1] PHILOS C G.Oscillation theorems for linear differential equations of second order[J].Arch Math,1989,53(1):482-492.
[2] JAROD J.An oscillation test for a class of a linear neutral differential equations[J].Math Anal,1991,159(1):406-417.
[3] YU Jian-she,WANG Zhi-cheng.Some further results on oscillation of neutral differential equations[J].Bull Austral Math Soc,1992,46(1):49-157.
[4] GUORI I.On the oscillatory behavior of solutions of certain nonlinear and linear delay differential equations[J].Nonlinear Analysis,1984,8(1):429-439.
[5] QIAN C,LADAS G.Oscillation in differential equations with positive and negative coefficients[J].Canad Math Bull,1990,33(1):442-450.
[6] MAGNUS W,WINKLER S.Hill′s equation[M].New York:Interscience Publishers,1966:23-28.
[7] National Bureau of Standards.Table relating to mathieu function[J].New York:Columbia University Press,1951:86-97.
[8] 史金麟.周期系数二阶线性微分方程的稳定性[J].数学物理学报,2000,20(1):130-139.
[9] 张俊祖,葛键.关于二阶线性齐次微分方程解的非振动性研究[J].西安联合大学学报,2001,4(2):40-43.
[10] 孔淑霞.二阶线性微分方程解的振动性[J].衡水学院学报,2010,12(1):1-4.

