延性材料全阶段单轴本构关系获取方法
姚 迪,蔡力勋,包 陈
(西南交通大学力学与工程学院,四川 成都 610031)
延性材料全阶段单轴本构关系获取方法
姚 迪,蔡力勋,包 陈
(西南交通大学力学与工程学院,四川 成都 610031)
材料拉伸直至破坏的单轴本构关系对于材料与结构的大变形分析和裂纹问题中的变形行为研究有重要意义。该文提出一种将实验与数值分析相结合获取材料拉伸直至颈缩破断全程本构关系的新方法——TF法(tensile test-finite element method)。通过构造初始微小缺陷实现拉伸试样的颈缩有限元模拟;应用自制对中夹具,结合DIC(digital image correlation)方法和应变传感器来测量材料拉伸全程的标距位移、试样颈缩根部直径和颈缩区轮廓线;应用逐步逼近原理并借助开发的ANSYS APDL命令流程序实现材料全程单轴真实本构关系求解的迭代计算。应用TF方法得到的全程材料本构关系对SS316L和T225NG合金拉伸试样的颈缩行为进行有限元模拟分析,结果表明:颈缩区两端的载荷-位移曲线、最小截面直径-位移曲线和颈缩区轮廓线的数值分析结果与实验结果吻合良好;对SS316L小曲率半径漏斗试样的载荷-位移曲线的模拟结果也与实验结果吻合良好。还给出SS316L和T225NG合金两种材料的Ramberg-Osgood全程单轴本构模型参数与等效破断应力应变,讨论两种材料单轴拉伸试样破断时颈缩根部横截面的应力分布。
TF法;单轴拉伸;颈缩;大变形;有限元模拟;材料本构关系
0 引 言
延性材料单轴拉伸试样颈缩后真应力-真应变曲线的获取对于材料与结构的大变形与断裂性能的数值分析十分重要。传统测试方法通常根据单轴试样拉伸实验得到工程应力应变关系,工程应力σE和工程应变εE分别定义为
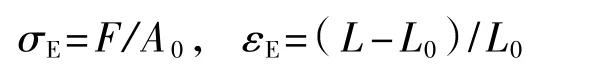
式中:F——拉伸载荷;
A0——拉伸试样的原始横截面积;
L0——用于测量拉伸变形的原始标距;
L——变形后的试样标距长度。
根据体积不可压缩理论可得拉伸试样的真应力σT和真应变εT的计算公式:
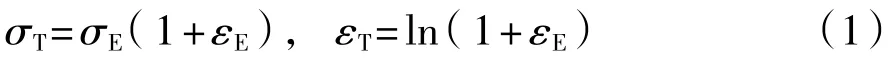
式(1)以试样等直段均匀伸长变形为基础推导而得,在颈缩发生后失效。
由于测试技术和分析方法的限制已有研究都是通过间接方式获取颈缩阶段的单轴本构关系。随着弹塑性有限元分析技术的发展,数值模拟被用于求取材料的全程εT-σT曲线,而其中关键技术就是对单轴拉伸试样颈缩现象的有效模拟。ZHANG[1]和Michael Briinig[2]等分别对颈缩现象进行了有限元模拟,由于早期的有限元工具能力有限,拉伸试样在颈缩阶段的模拟载荷P-V曲线同实验结果差异较大。近十年中,随着计算机技术与有限元商用软件的飞速发展,大大拓展了数值模拟方法解决力学问题的能力。Nilsson[3]的研究表明,低速加载下加载速率对材料颈缩无显著影响;Kazutake Komori[4]基于节点分离理论,实现了圆棒试样的单轴拉伸颈缩过程的数值模拟,但并未与实验结果进行比较。Tang等[5]基于损伤模型,尝试完成无缺陷的单轴拉伸试样颈缩模拟,但预测结果的精度尚未得到有效证明。Dumoulin等[6]利用光学测量获取的εT-σT实验曲线对板状拉伸试样P-V曲线进行了有限元模拟,其分析结果与实验结果符合程度欠佳。Peng等[7]为实现成型工艺中的大变形分析,用大变形本构模型,通过构造小缺陷对单轴拉伸试样进行了颈缩模拟,虽然颈缩前P-V曲线吻合良好,但对颈缩后的P-V曲线模拟效果不佳。Pino Koc等[8]讨论了多种本构关系理论与实验曲线的区别,采用计算机辅助识别和数学优化方法,获得了材料颈缩前的真实本构并预测了其颈缩行为。Giuseppe Mirone[9]建立了一种表征颈缩区应力应变特征的理论模型,并测定了颈缩区应力应变分布。然而,文献[8]和[9]所采用的本构关系曲线颈缩模拟结果均未与实验结果进行比较。基于单轴拉伸有限元数值模拟,ManSoo Joun等[10]通过刚塑性有限元法完成无缺陷单轴拉伸模型的颈缩模拟,逐点调整有限元中本构曲线使P-V模拟曲线与实验曲线一致,从而获取材料全程εT-σT曲线。然而,该方法采用自编刚塑性有限元程序且算法不易实现,仅由一个试样一种材料的P-V曲线计算获得的εT-σT曲线真实性与精度尚需验证。
文献[11]基于体积不可压缩理论提出了材料塑性变形微段分析法,给出了圆棒等直试样真应力和真应变计算公式:
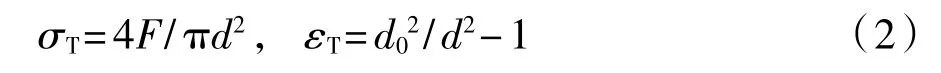
式中:d0——试样的原始截面直径;
d——试样颈缩细腰部的瞬时最小截面直径。
d值由DIC方法获得;然而,该方法将颈缩阶段最小截面上的应变作均匀分布假设尚缺乏有效性验证,比如,若此方法获得的d-V曲线与实验结果接近,所预测的P-V曲线是否必然符合实验,其合理性值得商榷。
本文系统地研究了构造初始缺陷诱发单轴拉伸试样颈缩的数值分析方法,完成了单轴拉伸颈缩现象的有限元模拟并获得拉伸试样颈缩区轮廓线,进而讨论了初始缺陷类型和尺寸对颈缩区轮廓线的影响。根据发展的颈缩分析方法,提出了一种结合实验和有限元分析获取全程单轴拉伸应力应变关系的新方法——TF方法。该方法结合单轴拉伸实验与有限元分析,通过应用自制对中夹具、应变引伸计和CCD等测试手段获得等直圆棒试样的真实拉伸变形,得到P-V、d-V曲线和不同位移下的颈缩区轮廓线,结合有限元APDL命令流程序和迭代方法获得试样颈缩后直至破断的材料等效本构关系曲线。基于该等效单轴本构关系进行有限元分析所得的P-V曲线、d-V曲线和颈缩区轮廓线均同实验结果吻合,从而实现了材料颈缩现象的真实模拟以及颈缩后直至破断时的真实应力应变的有效预测。
1 研究条件
1.1 实验系统
单轴拉伸实验系统包括MTS材料试验机(250kN,准确度5‰)、MTS632.12C-21应变引伸计(标距25 mm,量程50%,准确度5‰)、对中试样夹具和CCD光测系统。单轴试验系统及测试内容如图1所示。单轴拉伸实验采用位移控制加载,加载速率为0.02mm/s,等效应变速率约为500με/s。光测中,试样轮廓构形尺寸和最小截面直径采用Photoshop和GetData Grapher Digitizer测量,绝对误差不超过0.03mm。光测在夜晚进行,测试时,关闭室内普通照明灯光,安置定向光源照射白纸背景,产生均匀散射背景光源,以增加试样的对比度和几何尺寸测量精度。
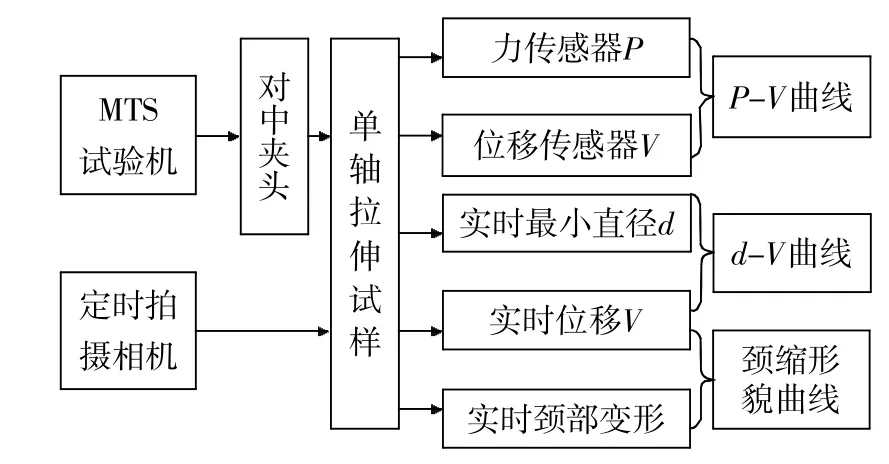
图1 实验系统框图
为消除偏心加载对实验结果的影响,拉伸试验机与试验机夹头间采用自制对中夹具连接,该夹具通过一个与试样螺旋相连的球形铰置入内端面含半球面的圆筒,实现试样与试验机铰链拉伸。自制对中夹具可有效消除拉伸实验偏心。图2为拉伸实验的实景照片(其中包括对中夹具、应变引伸计和散射光源等)。为了考查对中夹具系统的对中效果,对同一试样分别在4个方向测量弹性模量,结果表明各方向所测弹性模量直接误差小于0.5%。
1.2 材料与试样
实验采用SS316L不锈钢和T225NG钛合金两种材料,这两种材料的机械性能如表1所示,其化学成分如表2所示。单轴拉伸试样构形如图3所示,每种材料各采用两个试样。
2 TF方法求真应力-应变曲线
2.1 单轴拉伸试样颈缩行为的有限元模拟方法
延性材料拉伸试样表面因加工车痕等缺陷的存在使得其工作段难以达到理想等直状态,当拉伸载荷提升到一定程度后,试样含缺陷区域的变形逐渐超过无缺陷区域,颈缩现象会随之发生[12]。因此,含初始缺陷的拉伸试样有限元模型可有效模拟出颈缩现象[13]。
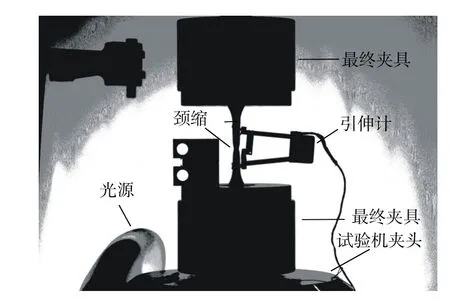
图2 拉伸实验实景

表1 材料机械性能

表2 SS316L和T225NG化学成分
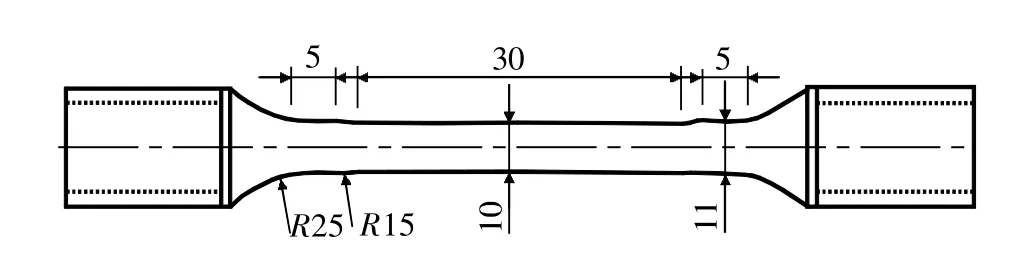
图3 拉伸试样几何构形(单位:mm)
图4(a)为5种表面含不同类型初始缺陷的(最大深度为δ)拉伸试样半剖面构形,假设颈缩由缺陷处发生,通过有限元方法对拉伸试样的颈缩行为进行模拟。
为研究缺陷类型及其最大深度δ对颈缩模拟的影响,图4(b)给出了试样半剖面有限元网格模型,图中还给出了颈缩的模拟情况。为保证有限元模拟精度,在缺陷处进行网格加密,在加密的10 mm2范围内,网格总数1120,节点数4505。
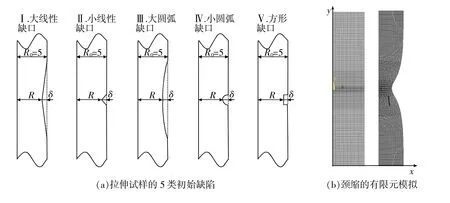
图4 拉伸试样的不同初始缺陷与颈缩模拟(单位:mm)
有限元分析中对单轴拉伸试样网格模型采用位移加载方式,对于含不同初始缺陷的试样模型,采用相同材料本构关系,在相同加载位移V下,计算不同缺陷类型和不同缺陷尺寸对颈缩区轮廓线和颈缩区最小横截面直径dmin的影响,如图5和图6所示。小尺寸缺陷下(δ=0.5μm),缺陷I和缺陷III试样由于有渐进过渡区,初始缺陷对颈缩轮廓线影响不显著;而在大尺寸缺陷下(δ=100 μm),初始缺陷引发的颈缩轮廓线差异较大。根据缺陷引发颈缩的尺寸效应,本文选择缺陷I进行有限元计算。不同δ值仅对颈缩发生后的最小截面尺寸dmin造成影响。
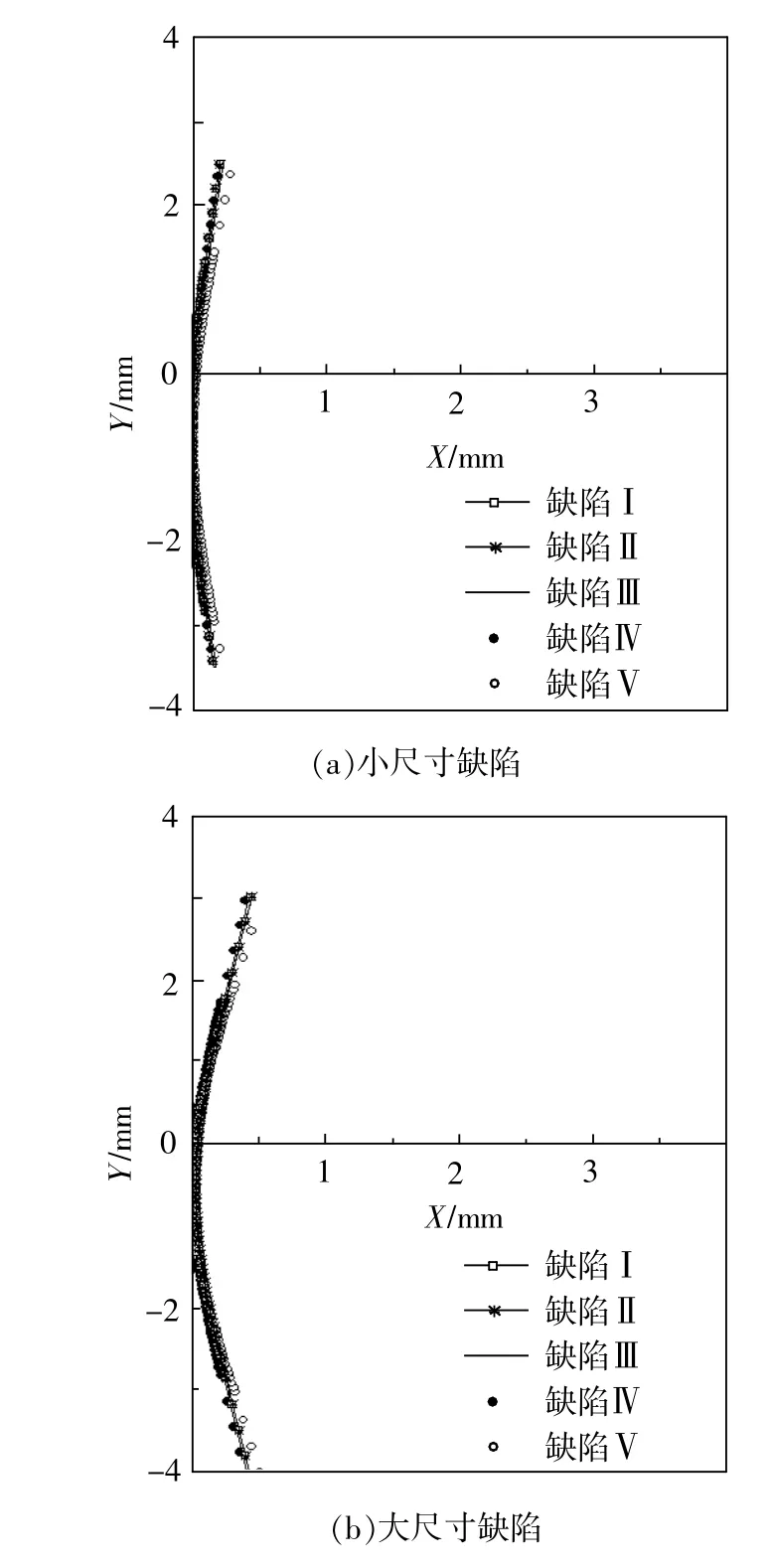
图5 V=16mm时颈缩区轮廓线的缺陷效应
图7给出了初始缺陷最大深度δ为0.04~1.0μm时,对应的V=16 mm和V=18 mm时有限元模拟获得的试样颈缩区最小截面直径dmin。由图7可知,当δ<0.2μm时,dmin不随δ变化而变化,当δ>0.2μm时,dmin随δ增大而逐渐减小。由此可知,初始缺陷尺寸对颈缩模拟的影响随δ的减小而逐渐消失,即建立含初始缺陷的拉伸试样可以对材料单轴拉伸实验全程进行精确模拟,缺陷尺寸变化对颈缩现象模拟的影响可忽略不计。
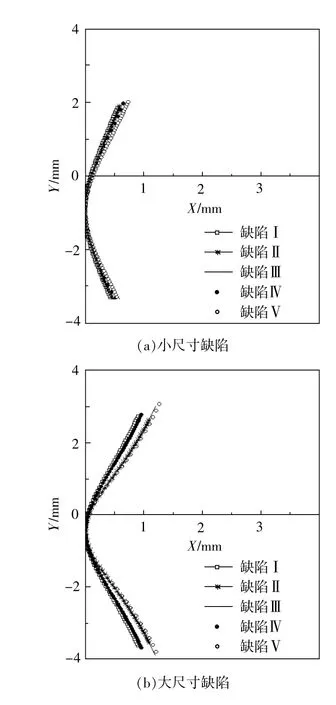
图6 V=18mm时颈缩区轮廓线的缺陷效应
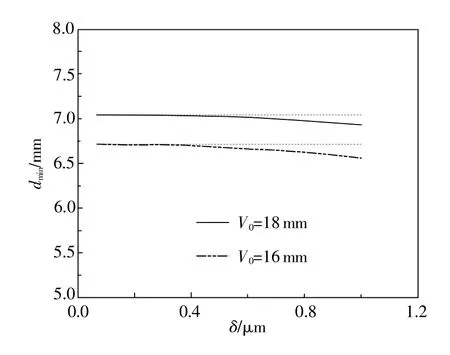
图7 初始缺陷尺寸对颈缩模拟的影响
经有限元分析可分别提取试样不同拉伸位移下的载荷P、颈缩根部横截面直径d和颈缩区形貌,由此绘出试样拉伸直至颈缩破断全程的P-V曲线、d-V曲线、颈缩区轮廓线的数值模拟结果。
2.2 不同材料本构关系曲线的真实性分析
根据SS316L单轴拉伸实验可直接获得材料工程应力应变曲线(Eng.curve),基于材料不可压缩理论可由SS316L单轴拉伸实验的未颈缩段获得R-O(ramberg-osgood)本构关系,称为TTCR(traditional true constitutive relationship),由文献[11]方法也可获得相应本构关系,图8给出了同一试样的3种本构关系曲线。由图8可知,不同方法得到的本构关系曲线在大变形时差异显著。

图8 SS316L本构关系的表征曲线
将TTCR曲线和文献[11]曲线作为本构关系分别用于有限元颈缩分析,计算得到拉伸试样含颈缩的标距段全程P-V曲线和全程d-V曲线。图9为两种曲线的模拟结果和实验结果。由图9可知,基于TTCR和文献[11]曲线所得的拉伸试样P-V和d-V模拟曲线均在颈缩发生后较大程度的偏离实验结果。若存在某种等效本构关系使得根据2.1节颈缩模拟获得的拉伸试样P-V曲线、d-V曲线和颈缩轮廓线与实验结果较为符合,则该等效本构关系可视为真实本构关系,而基于现行方法给出的TTCR和基于文献[11]给出的本构关系在颈缩发生之后将一定是失真的。
2.3 获取材料单轴本构关系曲线的逐步逼近模拟等效方法
由图9知,单轴拉伸实验P-V曲线和d-V曲线实验结果均处于基于TTCR曲线和文献[11]曲线的有限元模拟结果之间,由此假设,真实单轴本构关系曲线处于TTCR曲线和文献[11]曲线之间。由于材料不可压缩性,分析P-V曲线重合度,试样颈缩之前,单轴试样等截面标距段曲线TTCR与材料真实全程本构曲线重合。因此将TTCR定为参考曲线1,上调文献[11]曲线至颈缩点前重合为参考曲线2,如图10(a)所示。
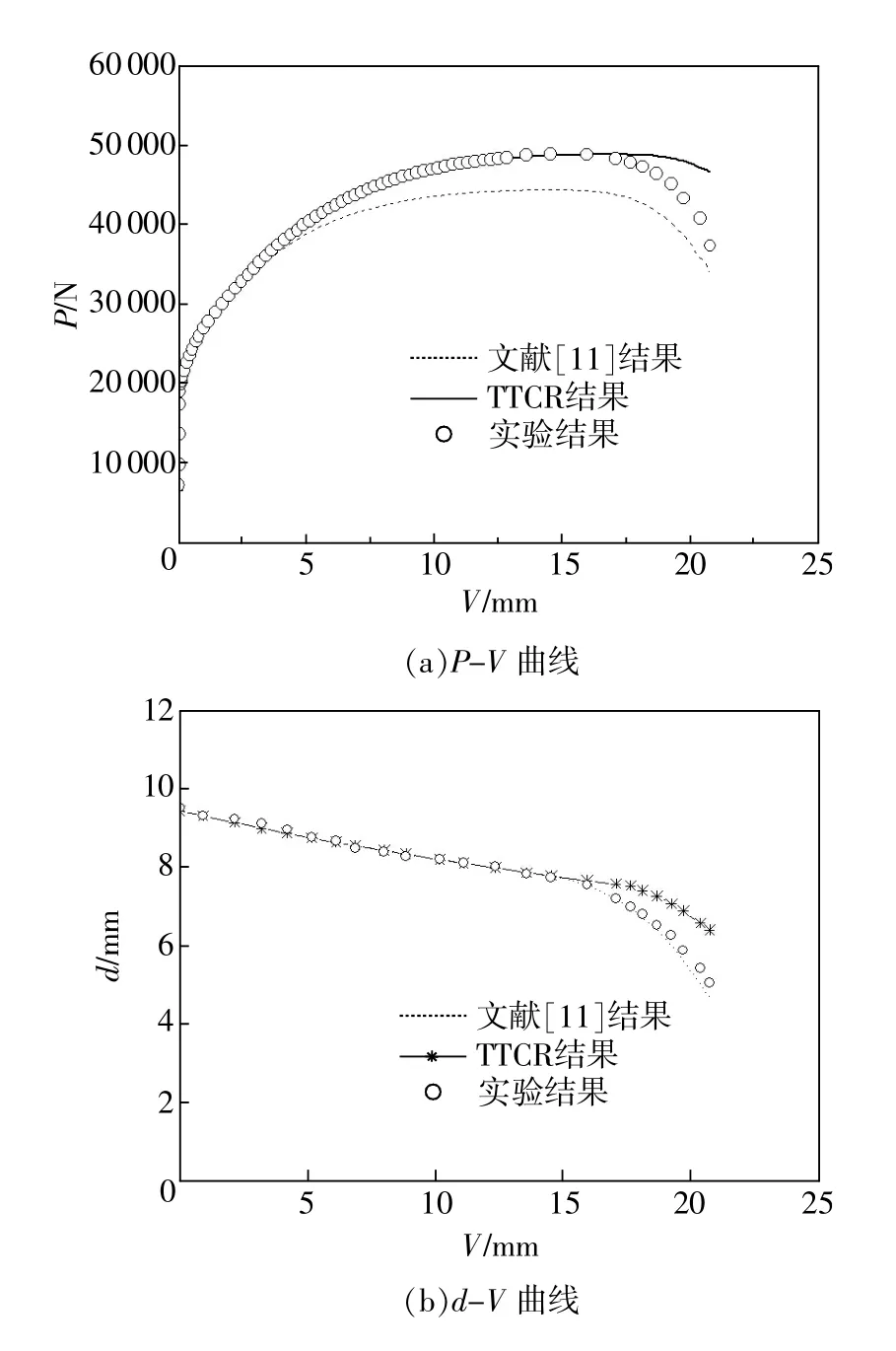
图9 现行方法的实验验证
以拉伸试样的d-V曲线或P-V曲线为判据,取两条本构关系参考曲线1和曲线2的均值为第1次迭代曲线,若获得的d-V曲线或P-V曲线在实验曲线与参考曲线1所获结果之间,则以第1次迭代曲线代替参考曲线1,以此类推使得有限元数值模拟的d-V曲线或P-V曲线与实验曲线逐次逼近。
完成SS316L和T225NG两组试样的单轴拉伸实验,以SS316L 1#试样为例详细阐述该方法的具体实施步骤:
1)分别以传统R-O本构关系曲线和文献[11]方法曲线,构造两条参考本构关系曲线,如图10(a)所示。
2)建立有限元模型,分别以两条参考曲线为单轴本构关系曲线,计算并绘出其P-V曲线。
3)设参考曲线1与参考曲线2的平均曲线为第1次迭代曲线(1st iterative result)如图10(a)所示;将第1次迭代曲线代入有限元模型中,计算其P-V曲线,第1次迭代曲线对应P-V曲线计算结果如图10(a)所示。
4)由图10(a)知,第1次迭代曲线比参考曲线1对应的P-V曲线更接近实际P-V曲线,以第1次迭代曲线代替参考曲线1,重复3)过程,直到模拟P-V曲线与实际曲线完全重合为止,如图10(b)中TF Result所示。
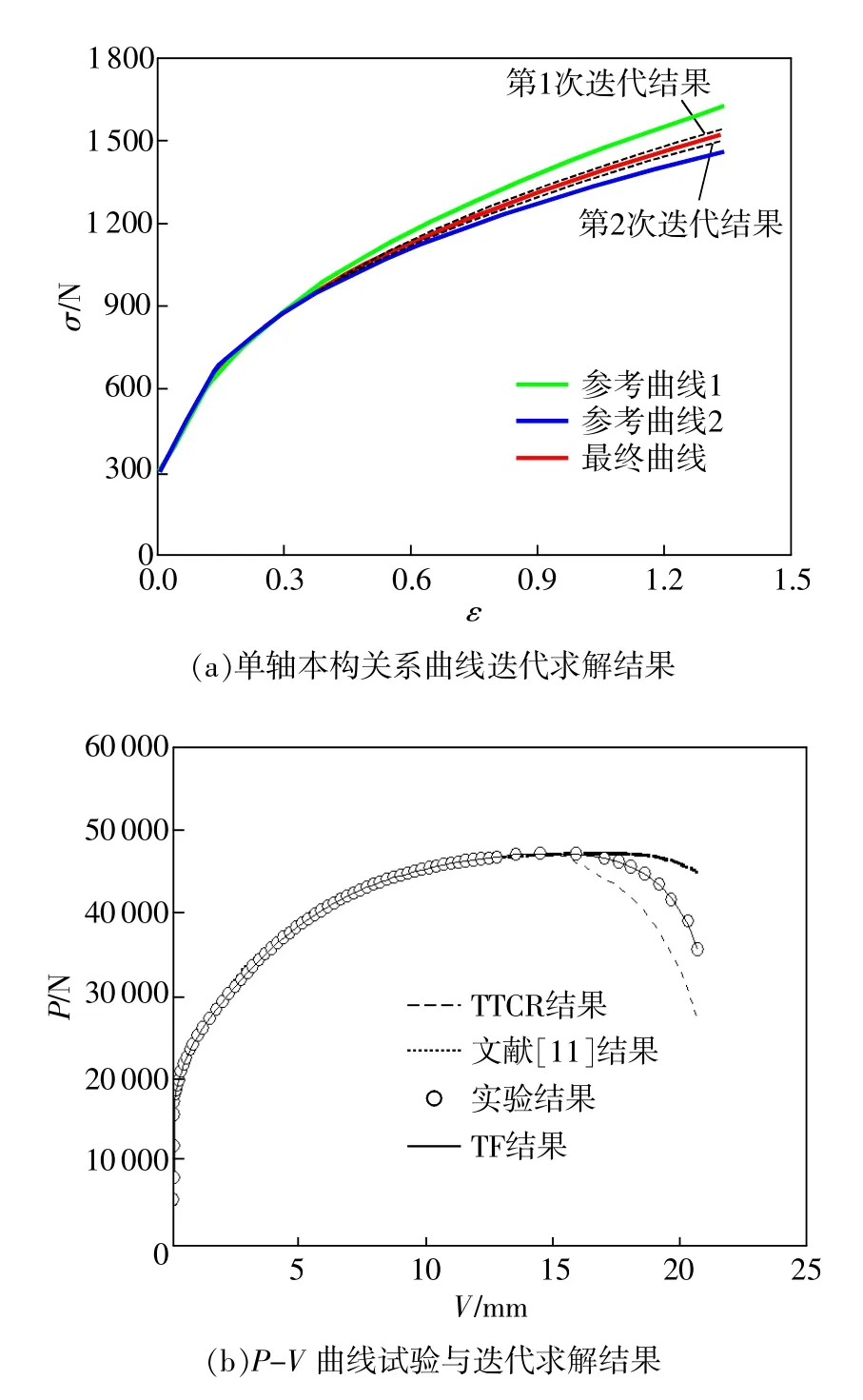
图10 迭代求解结果
5)用R-O模型拟合迭代求解得到等效的真实应力-应变曲线。
这种将单轴拉伸实验(tensile test)和有限元数值分析迭代(finite element method)结合求取材料单轴本构关系曲线的方法简称为TF方法。当然,根据该方法得到的材料单轴本构关系曲线有效性需要在不同方面经受实验验证。
3 不同单轴材料本构关系模型的有效性验证
如图10(b)和图11所示,使用TF方法得到的单轴本构关系曲线代入有限元计算中,得到的对应于SS316L的模拟P-V曲线、d-V曲线和颈缩区轮廓线与实验结果吻合良好。因此,由TF方法得到的本构关系曲线能够真实反映材料在拉伸全过程的变形特征,该曲线可以等效获得材料直至破断的真实本构关系。
另外,从图11(a)可以观察到参考曲线2(文献[11])虽然与d-V实验结果较为接近,但对应于图10(b)中的P-V实验结果在颈缩后却差异很大。因此,仅靠通过光测获得颈缩细腰直径与位移的变化获取材料本构关系是值得商榷的。

图11 SS316L拉伸试样d-V曲线与颈缩轮廓线的数值模拟结果与试验结果
由图10(b)和图11(a)也可以看到,基于传统实验方法获得的TTRC,代入有限元计算得到的d-V和P-V曲线在颈缩阶段与实验结果均不相符。
图12(a)~图12(c)给出了T225NG 1#试样TF方法求解得到的P-V曲线、d-V曲线以及颈部变形曲线同对应实验结果的比较情况。可见,所有求解曲线同实际光测曲线都吻合较好。
对于已完成的两个SS316L试样和两个T2525NG试样的单轴拉伸实验,用TF方法分别获取2#试样单轴拉伸本构关系曲线和P-V、d-V模拟曲线与实验曲线。图13给出了不同试样的P-V、d-V模拟曲线和实验曲线,可见由TF方法得到不同材料、不同试样的本构关系曲线得到的试样P-V、d-V曲线预测结果均与实验结果吻合良好。
4 直至破断的材料单轴大变形本构关系模型
对于符合幂律硬化特征的材料,其本构关系可用R-O模型描述:

式中:α——硬化系数;
n——硬化指数;
ε0——参考应变;
σ0——参考应力,通常取为流动应力。

图12 T225NG合金试验与模拟结果
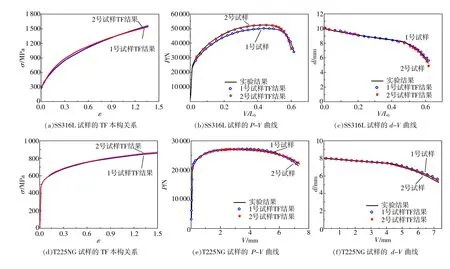
图13 基于TF方法的等效本构关系曲线(σ-ε)及其模拟获得的P-V曲线、d-V曲线与实验结果
即σ0=(σs+σmax)/2,对于传统单轴真应力-应变曲线,σmax取为抗拉强度σb,对于文献[11]和本文的等效真应力-真应变曲线,σmax取为破断时的应力σf。表3给出了分别根据传统方法、文献[11]方法以及本文TF方法得到的SS316L和T225NG合金的R-O模型参数,对应的应力-应变曲线如图14所示。
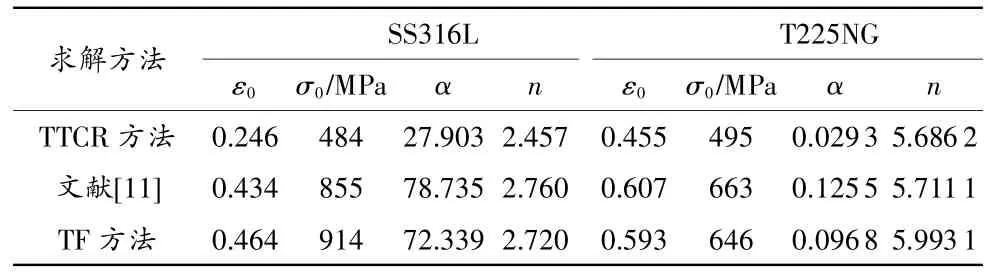
表3 不同求解方法获得的材料R-O模型参数比较
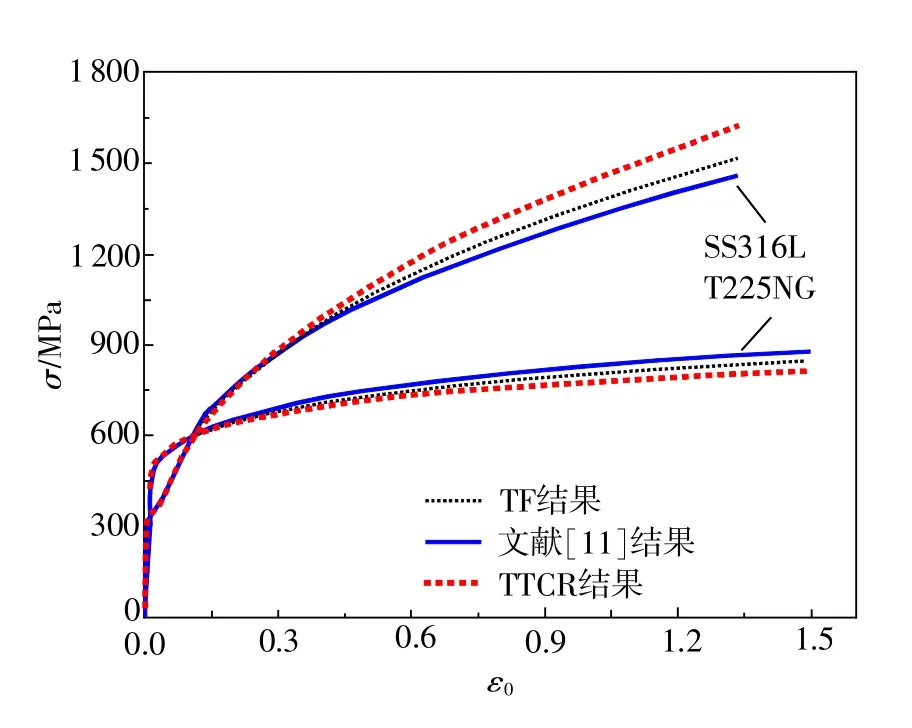
图14 两种材料不同试样下的本构关系
5 拉伸试样的破断应力应变分析
基于TF法获得的材料等效本构关系可对拉伸试样颈缩区最小横截面的应力分布进行分析。图15给出了SS316L的1#试样和T225NG的1#试样颈缩根部截面上的轴向应力σy、Von Mises等效应力σeq和切应力分布。图15中,x为细腰根部横截面中心到边缘的距离。当颈缩发生时,颈缩根部截面上应力分布不均匀,截面中心部位的应力大于根部应力。

图15 两种材料拉断时沿最小直径方向应力分布
设位移Vf为单轴拉伸试样破断时的标距段位移,可由有限元数值分析得到SS316L以及T225NG试样颈缩根部截面中心的最大轴向应力σymax,最大等效应变εymax,最大等效应力σeqmax,最大等效应变εeqmax,最大切应力,最大切应变γmax,相关结果由表4给出。
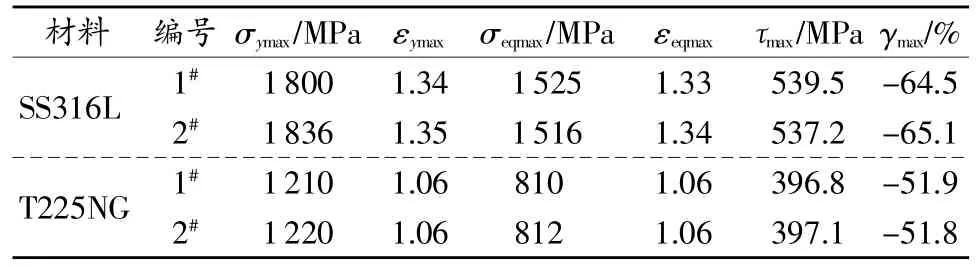
表4 两种材料的破断应力应变
按传统方法得到的 SS316L强度极限σb= 667 MPa,最大应变εmax=42%,T225NG强度极限σb= 550MPa,最大应变εmax=21%。可见,两种方法得到的最大应力、最大应变差异明显,因此TF方法得到的材料等效本构关系对于包括材料破断的大变形分析和裂纹断裂问题的精细分析有重要意义。
6 TF本构关系用于SS316 L漏斗试样大变形分析
在对中夹具上完成SS316L漏斗试样单轴拉伸实验,加载速率0.002 mm/s,获得P-V实验曲线,图16给出了漏斗试样尺寸构形。分别代入传统方法和TF方法获取的SS316L单轴本构关系,对实验过程进行有限元模拟,获得模拟P-V曲线,图17为漏斗试样的模拟变形图。

图16 SS316L漏斗试样(单位:mm)
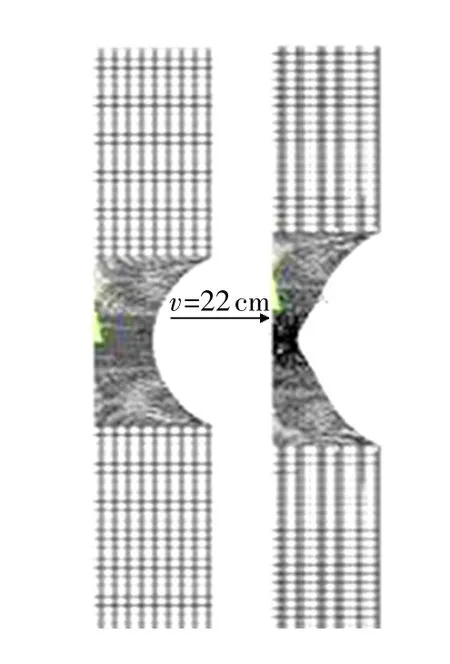
图17 漏斗试样变形的有限元模拟
如图18所示,与传统TTCR模拟得到的P-V曲线相比,由TF方法获取的模拟P-V曲线与实验曲线更为吻合,从而证明了TF方法的有效性。取最小横截面上最大应变绘制ε-P曲线对比可知,颈缩后的材料单轴本构关系对大变形分析影响较大。利用传统方法得到的最大应变εmax=84%,而利用TF方法得到的最大应变εmax=97%。可以看出,与TTCR方法相比,TF方法可以给出材料颈缩后的全程真实应力应变曲线、断点应力应变等关键数据,并且应用TF本构关系曲线进行有限元模拟计算,获得的材料变形特征曲线比TTCR的模拟结果更加接近真实情况。

图18 漏斗试样拉伸模拟结果
由图18可知,漏斗试样破断的实验载荷Pf= 43.2kN,根据TF方法预测得到的材料破断载荷Pf=45.7kN,与实验结果较为接近,利用TTCR本构关系预测得到的破断载荷Pf=47.7kN,与实验结果误差为10.41%。
7 结束语
1)提出了基于实验和有限元模拟获取材料本构关系的TF方法:应用微小尺寸缺陷有效模拟拉伸试样颈缩变形的有限元方法;采用自制对中夹具、应变引伸计和DIC变形测试技术获得拉伸试样颈缩过程中P-V曲线、d-V曲线和颈缩区轮廓线的实验方法;借助自编ANSYS APDL程序,提出以P-V曲线为判据获取材料单轴本构关系曲线的有限元逐步逼近求解方法。
2)对SS316L和T225NG,采用TF本构关系对单轴拉伸试样的P-V曲线、d-V曲线和颈缩轮廓线的有限元模拟结果均与实验结果吻合良好。
3)对SS316L,采用TF本构关系对小曲率半径漏斗试样P-V曲线的有限元模拟结果与实验结果较为吻合。
4)对SS316L和T225NG,应用TF方法得到了直至破断的Ramber-Osgood本构关系参数;给出了两种材料单轴拉伸试样颈缩达到临界破断时颈缩区最小横截面上的应力应变分布;给出了材料破断时的最大应力和最大应变。
[1]Zhang K S.Technical note fracture prediction and cecking analysis[J].Engineering Fracture Mechanics,1995,52(3):575-582.
[2]Briinig M.Numerical analysis and modeling of large deformation and necking behavior of tensile specimens[J]. Finite Elements in Analysis and Design,1998(28):303-319.
[3]Nilsson K.Effects of inertia on dynamic neck formation in tensile bars[J].European Journal of Mechanics-A/Solids,2001,20(5):713-729.
[4]Komori K.Simulation of tensile test by node separation method[J].Journalof Materials Processing Technology,2002,125(126):608-612.
[5]Tang C Y,Fan J P,Lee T C,et al.Simulation of necking using a damage coupled finite element method[J]. Journal of Materials Processing Technology,2003(139):510-513.
[6]Dumoulin S,Tabourot L,Chappuis C,et al.Determination of the equivalent stress-equivalent strain relationship of a copper sample under tensile loading[J].Journal of Materials Processing Technology,2003(133):79-83.
[7]Peng X,Balendra R.Application of a physically based constitutive model to metalforming analysis[J].Journal of Materials Processing Technology,2004(145):180-188.
[8]Koc P,Stok B.Computer-aided identification of the yield curve of a sheet metal after onset of necking[J]. Computational Materials Science,2004(31):155-168.
[9]Mirone G.A new model for the elastoplastic characterization and the stress-strain determination on the necking section of a tensile specimen[J].International Journal of Solids and Structures,2004(41):3545-3564.
[10]Joun M S,Eomc J G,Lee M C.A new method for acquiring true stress-strain curves over a large range of strains using a tensile test and finite element method[J]. Mechanics of Materials,2008(40):586-593.
[11]王长利.真应力-真应变计算模型及测试系统:中国,200810064955[P].2008-12-10.
[12]刘瑞堂,姜风春.单轴拉伸试样的颈缩过程及形变强化特性的影响[J].物理测试,1998(5):5-8.
[13]索忠林,刘颖.带缺陷试样的稳定性与颈缩解析[J].长春大学学报:自然科学版,2006,16(4):1-4.
Approach for full-range uniaxial constitutive relationships of ductile materials
YAO Di,CAI Li-xun,BAO Chen
(School of Mechanics and Engineering,Southwest Jiaotong university,Chengdu 610031,China)
The description of constitutive relationships of materials up to failure is very significant for the analyses of large deformation and fracture problems of engineering structures.This paper presents a new method to determine the full-range uniaxial constitutive relationship of a material. This approach combining tensile tests that lead to specimen necking and the finite element method is named as TF method.The method firstly implements the necking simulation of a tensile specimen by constructing an initial defect.And then the deformation of the specimen in gauge length range,the cross section diameter at necking root and necking contours of the specimen can be measured by using the self-made centering clamps,DIC (digital image correlation)technique and strain sensor.Finally,ANSYS APDL command stream program is developed to conduct the iterative solution of the constitutive relationship based on load versus displacement curve.The research results show that the necking simulation results of the specimens for 316L stainless steel and T225NG titanium alloy are much closed to the testing results.The simulation for a funnel specimen ofSS316L with smallcurvature radiusisinvestigated.Besides,the parametersof Ramberg-Osgood constitutive model and the failure stress distributions on the cross section at necking root of the specimens for the two materials are given.
TF method;uniaxial tension;necking deformation;large deformation;finite element simulation;constitutive relationship of materials
O346.1;TG113.25;TG142.33;TM930.12
:A
:1674-5124(2014)05-0005-09
10.11857/j.issn.1674-5124.2014.05.002
2014-04-09;
:2014-06-03
国家自然科学基金项目(11072205)
姚 迪(1990-),男,山东荷泽市人,博士,研究方向为材料本构关系与断裂力学。

