基于着色Petri网的双向搜索关键路径算法

□杨夏妮

（玉林师范学院 计算机科学与工程学院，广西 玉林 537000）

基于着色Petri网的双向搜索关键路径算法

□杨夏妮

（玉林师范学院 计算机科学与工程学院，广西 玉林 537000）

提出一种基于着色Petri网的双向搜索关键路径算法，首先将AOE网转换成带时间状态的着色Petri网，然后运行带时间状态的着色Petri网，分别从源点和汇点双向搜索关键路径，最后给出了对典型实例的仿真实验，结果验证了双向搜索关键路径算法的执行效率优于传统单向搜索关键路径算法.

着色Petri网；关键路径；双向搜索；AOE网

1 引言

AOE网（Activity On Edge）即边表示活动的网，是一个带权的有向无环图，其中顶点表示事件（Event），弧表示活动，权表示活动持续的时间，网中只有一个入度为零的点（叫做源点）和一个出度为零的点（叫做汇点）.通常，AOE网可用来估算工程的完成时间，求解关键路径的目的就是要找出影响工程进度的关键活动，从而采取有效措施缩短工期，提高效率.传统的关键路径的求解算法通过分别求出所有事件的最早和最迟开始时间以及每项活动的最早和最迟结束时间来求得关键活动.针对传统的求解算法计算复杂的基础上，国内外学者相继提出了一些新的方法在存储结构和搜索方法方面对传统的基于AOE网算法进行改进.根据算法采用的存储结构、算法的存储空间以及运算复杂度的不同，算法采用的存储结构主要可分为十字链表[1]、邻接矩阵[2,3]、稀疏矩阵[4]以及邻接表[5-8]等几种.根据搜索方法主要可分深度优先搜索[9]、广度优先搜索[1]和动态规划[8]等.以上的这些算法较之传统的基于AOE网算法节省了存储空间，具有更高的效率和更强的健壮性，但是基于Petri网的关键路径求解算法[10]利用Petri网理论将AOE网转换成带时间状态的Petri网，通过运行该网络并进行剪枝优化，自动获取关键路径，算法的执行效率比以上算法要高，更易于实现.本文在基于Petri网的关键路径求解算法的基础上，提出双向搜索[11-12]关键路径的方法，首先将AOE网转换成带时间状态的着色Petri网，然后通过运行带时间状态的着色Petri网来获取关键路径.本算法不仅能求出所有关键路径，而且时间复杂度方面略优于基于Petri网的关键路径求解算法.

2 基础理论

定义1着色Petri网（Colored Petri Net，CPN）可表示为一个五元组：CPN=(P,T,F,C,M0).其中：1）P={p1,p2,…,pn}为非空有限库所集，T={t1,t2,…,tm}为非空有限变迁集，且满足P∩T≠φ，P∪T≠φ；F⊆(P×T)∪(T×P)，F是CPN上的流关系，其元素叫弧；2）色彩集C={C(p),C(t)}，C(p)是与每个库所有关的色彩集，C(t)是与每个变迁有关的色彩集；3）M0为初始令牌集.

定义2设CPN=(P,T,F,C,M0)是一个着色Petri网.对于x∈P∪T，记

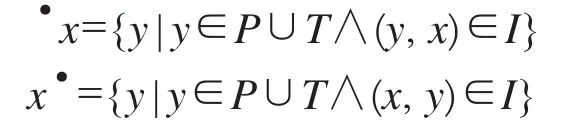
称·x为x的输入集，x·为x的输出集.

对定义1着色Petri网的色彩集基础上增加着色弧集（即色彩集C={C(p),C(t),C(f)}，C(f)是与每条弧有关的色彩集）和时间状态，提出带时间状态着色Petri网.

定义3带时间状态的着色Petri网（EtCPN）是一个二元组EtCPN=(CPN,DI)，其中∑是一个着色Petri网系统，DI是定义在库所集P上的时间函数，即DI∶P→R+，R+表示非负实数集.对于p∈P,DI(p)=a表示托肯将在p中至少滞留a个单位时间.

定义4设EtCPN=(CPN,DI)是一个带时间状态的着色Petri网，M0是CPN的初始标识，M∈R(M0)，则EtCPN的使能规则定义如下：在标识M下，色彩token只能沿着与其色彩一致的弧线移动，如果存在一个变迁t∈T，对于∀p∈·t，有M(p)≥1成立，则标识M能在变迁t发生；设发生后的标识为M'，记M能在变迁t发生后为M'这一过程为M[t>M'，则p中所含token在M'下的标签定义为(Max(M'(τip)))+DI(p)))，其中M'(τip)是t发生后由第i种色彩弧线传递而来的·t中托肯标签.

例1 给定如图1所示的带时间状态的着色Petri网系统EtCPN=(CPN,DI).

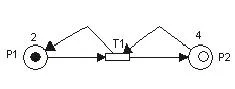
图1 变迁T1发生前的网系统EtCPN 

在图1所示的网系统EtCPN中，初始标识M0=(1,1)T，库所P1和P2中所含的token有2种色彩，弧线有2种色彩，分别用直线弧和折线弧表示，约定库所P1的token（实心圆）只能沿着直线弧移动，而库所P2的token（空心圆）只能沿着折线弧移动，下面的例子也采用这种约定.根据定义4的使能规则，标识M0能在变迁T1发生，发生后的标识M1=(1,1)T，记作M0[t>M1，则库所P1和P2中所含token在M1下的标签均为TokenFlag(6)，如图2所示.

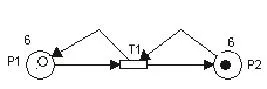
图2 变迁T1发生后的网系统EtCPN 

3 基于EtCPN 的双向搜索关键路径算法

3.1 算法实现

基于EtCPN的双向搜索关键路径算法的求解思路是：首先将AOE网转换成带时间状态的着色Petri网EtCPN，然后运行EtCPN网系统分别从源点和汇点同时双向搜索关键路径.

求解思路中需要解决两个关键问题：

（1）如何将AOE网转换成带时间状态的着色Petri网EtCPN？

（2）如何获取关键路径？

解决以上关键问题的解决方案如下：

（1）将AOE网转换成带时间状态的着色Petri网EtCPN的方法是：将AOE网中的顶点vj用变迁tvj来表示，弧线ek用库所pk来表示，弧上的权值作为库所pk上的时间函数，即DI(pk)=a.在EtCPN中构建两种不同色彩的有向弧，即直线弧和折线弧.构建两种不同色彩的token，即实心圆和空心圆，其中实心圆沿直线弧移动，空心圆沿折线弧移动.在原AOE网的源点转换成的变迁之前和汇点转换成的变迁之后各添加一个库所，并分别在这两个库所中添加一个实心圆token和一个空心圆token作为EtCPN的初始标识.

例2给定如图3所示的AOE网G=(V,E),其中v1,v3,…,v9表示事件，事件v1表示工程的起点，事件v9表示工程的终结，，ai(i=1,2,…,11)表示活动ai持续的时间.

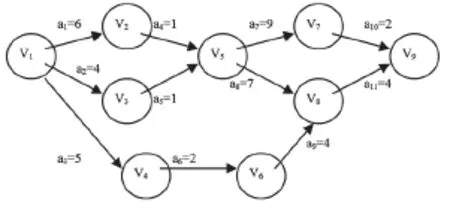
图3 一个AOE网

将AOE网转换成带时间状态的着色Petri网EtCPN如图4所示.

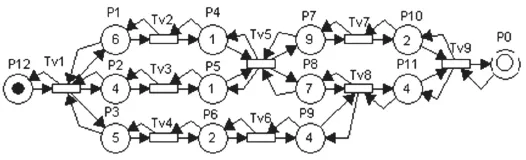
图4 AOE网转换的EtCPN 

（2）在所有关键路径获取的研究中，都是通过单向搜索的，因此本算法尝试进行双向搜索，即从AOE网中的源点和汇点同时进行搜索.

因为该算法是并行的，在运行的过程中会出现结点重复搜索的现象，为了避免产生该现象，所以规定在运行EtCPN过程中，当某个库所的token个数为2或变迁的输入集和输出集的token个数均为1时，就停止该token的前进.

本算法对于双向搜索关键路径结束的判定条件如下：当所有变迁都发生一次或者（只有一个变迁还未发生且该变迁的输入集和输出集的token个数均为1）时，则结束搜索，最后一个停止前进token的变迁发生序列就为关键路径.该条件的正确性由定理1得证.

定理1给定由AOE网转换成的带时间状态的着色Petri网系统EtCPN=(CPN,DI) ，设flag(tvj)为变迁tvj是否发生的标志，flag(tvj)的取值范围为{true,flase}，其中flag(tvj)=true表示变迁tvj已经发生，flag(tvj)=flase表示变迁tvj还未发生，（1）如果∀tvj∈T,flag(tvj)=true，则最后一个停止前进的token所在库所的的值就为关键路径的长度，而Max(M'(τip)的变迁序列就为关键路径.（2）如果∀tvj(i=1,2,j-1,j+1,…,m),flag(tvj)=true)∧(∃pi,pk∈P,∃tvj∈T,pk·=·pi=tvj∧flag(tvj)=flase)∧(M(pi)=M(pk)=1)，则最后两个停止前进的token所在库的TokenFlag(Max(M'(τipi))+D(p))与TokenFlag(Max(M'(τipk))+D(pk)的和就为关键路径的长度，而Max(M'(τipk))的变迁序列再加上tvj就为关键路径.

证明：（1）因为在EtCPN中，∀tvj∈T，flag(tvj)=true表示所有的变迁均发生一次，当∃pk∈P,M(pk)=2时，说明这两个token一个是实心圆token，一个是空心圆token，则分别来自于直线弧和折线弧；又因为在中，Max(M'(τip))总是取t发生后由第i种色彩弧线传递而来的·t中最大托肯标签，所以说明其TokenFlag的值最大，即所花的时间最多，根据关键路径的定义：路径长度最长的路径叫做关键路径，所以最后一个停止前进的token所在库所的(Max(M'(τip)))+DI(p)的值就为关键路径的长度，Max(M'(τip))的变迁序列就为关键路径.

（2）因为在EtCPN中，∀tvj(i=1,2,j-1,j+1,…,m),flag(tvj)=true)表示所有变迁tvi除变迁tvj外均已经发生一次，则说明在变迁tvj的输入库所和输出库所的token运行的时间最长，所以变迁tvj的输入库所pi和输出库所pk的TokenFlag((Max(M'(τipi))+D(pi)与TokenFlag((Max(M'(τipk))+D(pk)的和就为关键路径的长度，而Max(M'(τip))的变迁序列再加上tvj就为关键路径.原理证毕.

算法1 基于EtCPN的双向搜索关键路径算法

输入：一个AOE网G=(V,E)，V中顶点代表事件，E中弧代表活动，弧上的权值a表示活动持续的时间，其中vi表示工程的起点，v0表示工程的终结；

输出：网中的关键路径.

算法步骤：

4. 输出变迁序列和max值，其中变迁序列即为网中的关键路径，max的值即为网中关键路径的长度.

3.2 时间复杂度分析

假设需求解的AOE网G中含V个顶点、E条边，其中|V|=m，|E|=n，基于EtCPN的双向搜索关键路径算法的第一步近似认为可在单位时间内完成，第2步和第4步在单位时间内完成，第3步基本上需遍历所有的变迁和库所，所以总的时间复杂度为O(m+n)，与基于Petri网的关键路径求解算法的时间复杂度一样，和传统的AOE网的求解算法相比，其时间常数因子略小一些.

3.3 实例分析

例3 求出例2中给定的AOE网G=(V,E)的关键路径.

解题步骤如下：

1. 将G转换成带时间状态的着色Petri网EtCPN，如图4所示.

2. //初始化

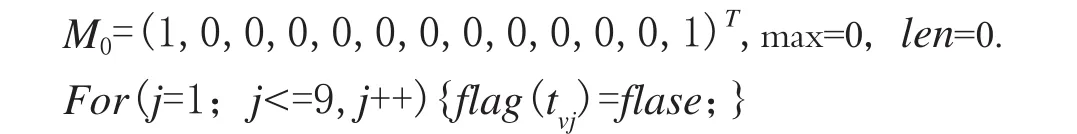
3.根据变迁的使能规则运行EtCPN网系统.变迁序列δ1=tv1tv9发生，有M0[δ1＞M1，标识M1=(0,1,1,1,0, 0,0,0,0,0,1,1,0)T.flag(tv1)=flag(tv9)=true，

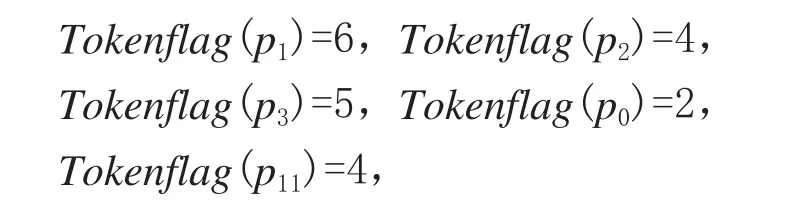
4.变迁序列δ1=tv2tv3tv4tv7tv8发生，此时需等待p1、p2、p3、p10和p11中所含托肯标签的计数达到.有M1[δ2＞M2，标识M2=(0,0,0,0,1,1,1,1,1,1,0,0,0)T

此时首先变迁tv6满足token停止前进的条件，则记录变迁序列为tv1tv4tv6tv8tv9，len=Tokenflag(p6)+Tok enflag(p9)=5.max=5.接着变迁tv5满足token停止前进的条件，则记录变迁序列为tv1tv3tv5tv7tv9或tv1tv3tv5tv8tv9或tv1tv2tv5tv7tv9或tv1tv2tv5tv8tv9，

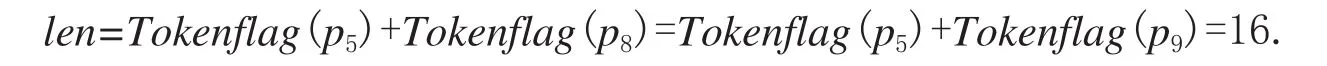
或

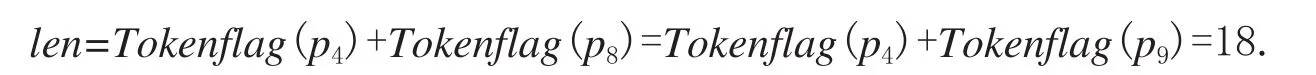
则 max=18.

5.输出变迁序列tv1tv2tv5tv7tv9或tv1tv2tv5tv8tv9和max的值18，即关键路径有两条tv1tv2tv5tv7tv9或tv1tv2tv5tv8tv9，关键路径长度为18.

4 仿真实验

为了验证基于EtCPN的双向搜索关键路径算法的正确性和有效性，首先分别计算用基于Petri网的关键路径求解算法和基于EtCPN的双向搜索关键路径算法求解例3所需的时间，用基于Petri网的关键路径求解算法例3所需时间为V+E+V+(7/11)E=36个单位时间，而用基于EtCPN的双向搜索关键路径算法所需时间为V+E+(1/2)V+(1/2)E=30个单位时间.接下来对算法进行仿真实验，实验环境为Window XP，使用一台Intel Core i3 3240，CPU 3.4GHZ，2GB内存PC机进行，Petri网的仿真工具采用CPN tool.根据图4的EtCPN建立模型，并设定各个库所延迟的时间，最后运行该模型.运行结果逼近于理论上的运行时间，从而证明基于EtCPN的双向搜索关键路径算法略优于基于Petri网的关键路径求解算法.

5 结束语

对于国内外学者对关键路径的算法的研究都是基于单向搜索的，本文中的算法尝试对关键路径的求解提出双向搜索，即从AOE网的源点和汇点同时搜索，而Petri网是一种对并行系统进行描述和建模的重要图形化数学工具，能够描述系统的功能和动态行为，对于分布式、并行系统建模尤为合适，因此本文提出了一种基于着色Petri网的双向搜索关键路径的算法，首先将AOE网转换成带时间状态的着色Petri网，通过运行带时间状态的着色Petri网双向搜索来获取关键路径.通过实例分析，验证了该算法不仅能求出所有关键路径，而且时间复杂度方面略优于文献[10]的算法，这对于解决帮助分析关键路径争取提高关键活动的工效来缩短工期具有重要的意义. ■

[1]徐凤生，黄倩.关键路径求解的新算法[J].计算机应用，2004，24（12）：108-109.

[2]Chen Shipin． Analysis of critical paths in a project network with fuzzy activity times[J]． European Journal of Operational Research, 2007, 183(1):442-459．

[3]徐凤生.一种求关键路径的新算法[J].计算机工程与应用，2005，24（6）：82-84.

[4]林铭德，戴一景.基于EVM矩阵求解关键路径的方法[J].武汉理工大学学报，2012，34（6）：690-694.

[5]Li Tinazhi． A novel algorithm for critical paths[J]． 2009 WRI World Congress on Computer Science and Information Engineering, 2009(1): 226-229．

[6]王明福.一种求解关键路径的新算法[J].计算机工程，2008，34（9）：106-108.

[7]胡美群，夏银水，王伦耀.基于分支限界的关键路径求解算法[J].宁波大学学报，2011，24（2）：37-41.

[8]刘芳，王玲.基于动态规划思想求解关键路径的算法[J].计算机应用，2006，26（6）：1440-1442.

[9]孟繁桢.求关键路径的一个算法[J].计算机工程，1995，21（4）：6-9.

[10]叶双，叶剑虹，刘传才.基于Petri网的关键路径求解算法[J].计算机科学，2012，39（6）：201-203.

[11]贾珺，孙静瑜，候冰.基于双向搜索的运输路线优化算法[J].军事运筹于系统工程，2010,24（4）：61-64.

[12]任晓翠.基于双向搜索算法的物流配送最短路径优化研究[J[.东方企业文化，2013,4：231-232.

【责任编辑 谢明俊】

Algorithm for Bidirectional Searching for Critical Paths Based on Colored Petri Net

YANG Xia-ni
(School of Computer Science & Engineering, Yulin Normal University, Yulin, Guangxi 537000)

The paper proposed the algorithm for bidirectional searching for critical paths based on Colored Petri Net． Firstly, the AOE net was converted into the Colored Petri Net with time state． Second, Colored Petri Net with time state was operated from the source and the sink to search for the critical paths． Finally, the simulation experiment of the typical examples was given． The experimental result verified the execution efficiency of the algorithm for bidirectional searching for critical paths based on colored petri net is better than the traditional algorithm for one-way searching．

Colored Petri Net; critical path; bidirectional searching; AOE net

TP393.027

A

1004-4671（2014）02-0100-06

2014-01-01

广西壮族自治区教育厅科研立项项目（201106LX515）。

杨夏妮(1980～)，女，广西玉林人，玉林师范学院计算机科学与工程学院讲师，主要研究方向：Petri网理论及应用研究。