集装箱码头泊位-岸桥集成分派干扰管理的分层调整策略

林庆福，胡志华,2，陶 莎

(1. 上海海事大学 物流研究中心，上海 201306；2. 同济大学 经济与管理学院，上海 200092)

0 引 言

集装箱码头泊位-岸桥集成分派难以考虑船舶抵港的不确定性。集装箱码头在国际物流和国民经济中具有不可替代的战略性地位，是国际物流中不可或缺的重要节点。随着经济全球化进程加快，这种重要性日益突出。然而，在全球集装箱运输业高速发展的同时，由于各种不可抗力或者人为因素导致了集装箱船航行时间的不确定性，从而造成船舶抵港时间的不确定性，这就容易打乱了码头已有的泊位与岸桥集成分派计划。由于码头泊位和岸桥等作为稀缺资源，泊位和岸桥的可配置资源有限，这就需要对原计划进行调整。这种情况对原有系统造成干扰，成本的增加也不可避免。如何实时有效地解决这类干扰事件，使干扰事件对整个集装箱码头作业系统产生的扰动最小，是当前集装箱码头运营管理中的一个重要问题。

干扰管理(Disruption Management)是一种实时处理这类问题的方法，G.Yu，等[1]对干扰管理的定义为：针对实际问题和干扰事件的性质，建立相应的优化模型和有效的求解算法，快速、及时地给出干扰事件的调整计划。与重调度方法相比，该调整计划不是完全彻底地重新进行建模和优化，而是快速生成对系统扰动最小的调整方案；J.Clausen，等[2]也把干扰管理限定在使变化回归到最初计划这一基本目标之上，使系统扰动最小；胡祥培，等[3]概述了干扰管理理念的形成及其发展过程，综述分析了干扰管理的图模型和数学模型的研究进展，评述了干扰管理模型的求解算法，最后探讨了干扰问题的进一步研究方向；P.T.Evers[4]和S.M.Hong-Minh，等[5]研究了如何在供应链和物流活动中有效降低干扰事件造成的新增成本。目前，干扰管理思想已经在航班计划、物流配送、机器生产调度、供应链协调、项目管理等领域得到了广泛应用[6-10]。

Y.M.Park，等[11]提出连续泊位与岸桥的协调调度问题，并设计了两阶段求解算法：第1阶段解决了每艘船舶的靠泊位置和时间，以及分配的岸桥数量，用次梯度优化技术获得了近似最优解；第2阶段，利用动态规划的方法将具体岸桥分配给指定的船舶。韩晓龙，等[12]将连续泊位配置问题抽象为二维装箱问题，建立了同时考虑泊位和岸桥资源的整数规划模型。M.F.Monoaca，等[13]通过考虑船舶总的在港时间，建立了一种连续泊位动态分配模型并进行求解。P.Legato，等[14]基于船操作时间和岸桥使用量最小为目标，考虑船偏好泊位和时间，设计了随机动态环境中的DES模型。G.Giallombardo，等[15]将联合调度分为两步：第1步是将每个岸桥信息配置给每条船；第2步分配相应的泊位。周鹏飞，等[16]针对船舶抵港时间和装卸时间的随机性，建立了面向随机环境的集装箱码头泊位-岸桥分配模型，并设计一种改进的遗传算法进行求解。曾庆成，等[17]运用干扰管理方法，从码头作业成本、船舶等待成本、计划偏离度3个方面度量系统扰动，建立泊位分配-装卸桥调度干扰管理模型，设计局部重调度与禁忌搜索算法的仿真优化算法。杨春霞，等[18]针对因干扰事件引发的集装箱码头连续泊位分配计划问题，也提出了相应的干扰管理决策方法：在干扰事件发生前后，首先确定干扰事件的性质，并选择合适的恢复策略；在此基础上，建立综合考虑新计划性能、恢复成本和与原计划偏离度等3方面的扰动恢复模型，并采用多目标遗传算法进行求解，从而获得新的分配计划。

现今的国内外学者对泊位-岸桥分配调度方面的研究已有很多，对干扰管理问题的研究也有不少，但通常分开考虑泊位和岸桥的调整策略，没有考虑到干扰事件的不可预测性，以及偏差程度的影响。因此，在前人研究的基础上，笔者着重研究在初始码头泊位-岸桥分配调度的基础上，针对延期抵达船舶不同偏差程度，考虑基于泊位和岸桥调整的分层调整策略，以最大程度地降低码头作业系统所受到的干扰，保证码头作业的顺利进行。

1 问题定义与分析

1.1 泊位-岸桥分配调度

集装箱码头泊位-岸桥集成分派是指码头操作人员根据一定周期内的到港船舶信息，包括船舶基本参数以及装卸作业量和预计到达时间等，安排待靠泊船舶的靠泊位置和靠泊时间，以及作业岸桥等资源，使到港集装箱船能够合理、有序的靠泊，提高港口设施的装卸效率，完成靠港船舶的作业任务，及时离港。集装箱码头船舶作业过程如图1。

根据是否划分码头泊位将泊位-岸桥分配调度问题分为离散型泊位[19-22]和连续型泊位[23-25]两个方面。最初，主要是以离散型泊位的研究为主，后来由于集装箱船的大型化、差异化发展，同时为了使码头泊位、岸桥等资源得到充分利用，连续型泊位开始成为集装箱码头发展的趋势，连续型泊位-岸桥调度的研究也得到越来越多的重视。

连续型泊位-岸桥集成分派问题实际上就是要确定船舶的靠泊位置和靠泊时间，以及各船舶的作业岸桥数。Y.M.Park，等[11]在解决连续泊位的泊位岸桥集成调度问题中，将连续岸线离散化，建立了以时间为横轴，泊区为纵轴的二维坐标系。每个矩形表示一条船舶的停泊计划，横坐标表示停泊时间，纵坐标表示停泊位置，船舶停泊位置和停泊时间都是连续的，每条船舶只能占用一个矩形。每一个矩形的长度取决于作业时间不定，它与分配给它的岸桥数量成反比关系。韩晓龙，等[12]提出了连续泊位二维装箱问题把泊位-岸桥集成分派问题抽象化，在一个时间-泊位二维坐标轴中直观的表示各船舶的靠泊位置和作业时间。

1.2 干扰调整策略分析

集装箱船在航行过程中，容易发生诸如恶劣天气、机械设备或操作不当等干扰事件。在这种情况下，因为码头作业系统中的干扰事件导致其后船舶的靠泊作业计划受到一定程度的影响，成本的增加也不可避免。如何采取及时有效的措施应对这种不确定性，对码头作业的顺利进行至关重要，主要的受扰恢复策略有以下两种：

1)当干扰事件影响较小时，采取局部调整策略，通过泊位-岸桥分配计划自身的鲁棒性消除时间带来的负面影响。可以让延期抵达船舶在不影响其后所有船舶按原计划靠泊作业的情况下及时离港。此种情况下，可采取两种调整方法：①提高岸桥的作业效率，加快装卸进度，如让原先岸桥作业效率为25 TEU/h，增加到30 TEU/h；②增加该船的作业岸桥数，加快作业效率，但是不能超过船舶的同时作业最大岸桥数限制，以期让船舶按时离港。包括两种具体措施：调用备用岸桥，将同一时间段作业不受影响的其他船舶岸桥转移一部分到延期抵达船舶上。

2)当干扰事件影响程度较大时，已经不能通过自身调整恢复时，这时只能采取重调度策略，重新编排本船及之后船舶的泊位-岸桥分配计划，选取新增加的成本最小的方案。但是这种调整策略会造成整个系统较大的改动，有时候也会引起各方的利益冲突，实践中也较少采用。也可以让其他船舶按原计划靠泊作业，之后安排该船的靠泊作业。

鉴于局部调整策略有时因偏差程度过大无法完成调整，而重调度策略又容易损害到各方的利益，因此这里提出分层调整策略。分层调整策略，是介于局部调整策略和重调度策略之间的一种策略，即将所有可能受影响的船舶按先后顺序进行层级划分(图2)，将最先延期抵达船舶1～船舶3分为第1层(船舶1和船舶3因船舶2延期作业岸桥增加而受到岸桥总数约束的影响)；同理，船舶4～船舶6分为第2层，船舶7～船舶9分为第3层。当干扰船舶不能在之后船舶抵达前局部调整完，就采取重调度策略，无疑对整个系统造成较大的变动。因此，考虑尽可能使整个码头系统的扰动最小，按层级进行调整，以完成作业任务。

由于船舶延误时间的不可预测性，必须针对不同情况采取不同层次的调整策略。首先考虑第1层的调整，通过提高岸桥作业效率和增加作业岸桥数，让船舶2在09:00前通过局部调整策略完成靠泊作业离港，若无法在第2层级船舶靠泊作业前完成调整，则将第1层和第2层受影响船舶统一考虑，在第3层船舶靠泊前完成作业任务。依次类推，若到最后一层前仍无法完成调整，则采取重调度策略，编排各船舶的靠泊作业计划。

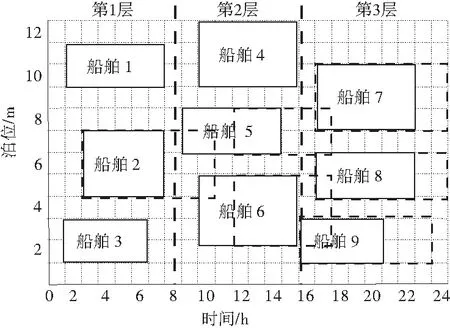
图2 干扰事件影响下泊位-岸桥分配示意Fig.2 Assignment schematic of berth-crane allocation in the case of interference

2 模 型

在Y.M.Park，等[11]的模型基础上，为了便于建模和分析，采用类似的假设：

1)所有待靠泊的船舶没有物理或技术上的限制，可以靠泊码头任何区域进行作业。

2)船舶的装卸时间以作业所需要的总岸桥时数计算，所有岸桥具有同质性，岸桥平均作业效率不受同时作业岸桥数量的影响，作业过程岸桥不发生故障，允许岸桥中途撤离该船的作业。

3)码头上的岸桥均位于同一轨道上，可以进行横向移动，岸桥水平移动的时间忽略不计。

4)船舶最左端(船头)为船舶的靠泊位置，且每艘船舶都有一个偏好靠泊位置。

5)每艘船靠泊的泊位长度和时间跨度以整数计，超过部分取完整单位。并且，考虑到重调度策略会严重损害各船公司和货主的间接利益，在条件允许的情况下必须选择分层调整策略，以采取分层调整所增加的成本最少作为最优调整策略。

2.1 符号说明

笔者在建模时仅考虑船舶靠泊位置和时间等偏差带来的惩罚成本。考虑船舶尺寸，以及船公司与码头的契约，每艘船舶设有同时作业的最大岸桥数和最小岸桥数。

2.1.1 集 合

1)sv={1,2,…,v}为船舶集合；

2)st={1,2,…,t}为时间分段集合；

3)sp={1,2,…,p}为靠泊位置集合。

2.1.2 参 数

1)对k∈sv，ek表示船舶k的预计到达时间；ak表示船舶k完成作业所需岸桥时；dk表示船舶k的预计离开时间；bk表示船舶k的长度；rk表示船舶k的偏好泊位；uk表示可以同时为船舶k作业的最多岸桥数；lk表示同时作业的最小岸桥数。

2)对k∈sv，c1k表示船舶k偏离偏好泊位每单位距离的惩罚成本；c2k表示船舶k抵港后等待的单位时间惩罚成本；c3k表示船舶k延迟离开每单位时间的惩罚成本。

3)常数C表示可利用的岸桥总数；M表示一个比较大的正常数。

2.1.3 决策变量

1)BLk表示船舶k左偏离偏好泊位的距离；BRk表示船舶k右偏离偏好泊位的距离；TLk表示船舶k抵港等待作业时间；DLk表示船舶k的延迟离开时间。

2)Yki表示在船舶k在时刻i分配到的岸桥数。

3)Ck表示船舶k上集装箱作业完成的时间。

4)Xkij为0-1变量，当方格(i，j)在船舶k靠泊作业的大矩阵中时为1；否则为0。

5)Zkij为0-1变量，当(i，j)位于靠泊作业大矩阵的左下顶点时为1；否则为0。

6)Vki为0-1变量，等于1表示船舶k在时刻i作业；否则为0。

10)Oki表示船舶k在时刻i正常作业的岸桥数量。

11)Pki表示船舶k在时刻i负荷作业的岸桥数量。

12)Qki表示船舶k在时刻i所使用的备用岸桥数。

2.2 模型建立

2.2.1 泊位-岸桥集成分派模型

在上述模型假设和符号说明的基础上，构造一个连续型泊位-岸桥集成分派模型，目标使得整个时期内所有船舶靠泊时间、位置偏差所受到的惩罚成本最少。连续型泊位-岸桥集成分派的模型建立如下：

minimizef=f(fc1,fc2,fc3)

(1)

f≥fc1+fc2+fc3

(2)

(3)

(4)

(5)

式(1)是模型的目标函数，表示船舶的各项惩罚成本之和最少，由3部分成本组成。式(3)～式(5)规定了船舶的各项惩罚成本。

以上目标函数需满足如下约束：

∀k∈sv:BLk≥rk-Bk

(6)

∀k∈sv:BRk≥Bk-rk

(7)

∀k∈sv:TLk≥Tk-ek

(8)

∀k∈sv:DLk≥Ck-dk

(9)

∀k∈sv:Tk≥ek

(10)

∀k∈sv,i∈st:Ck≥Vki(i+1)

(11)

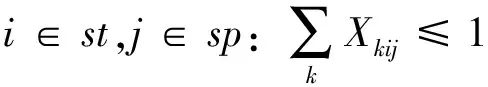
(12)

(13)

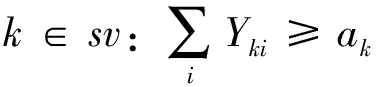
(14)

∀k∈sv,i∈st:Vki≤Yki

(15)

∀k∈sv,i∈st:Yki≤MVki

(16)

∀k∈sv,i∈st:Yki+M(1-Vki)≥lk

(17)

∀k∈sv,i∈st:Yki≤uk

(18)

(19)

(20)

∀k∈sv,ia∈st,ib∈st,ia1,ia>ib:

(21)

(22)

∀k∈sv,i∈st,j∈sp:Vki≥Zkij

(23)

(24)

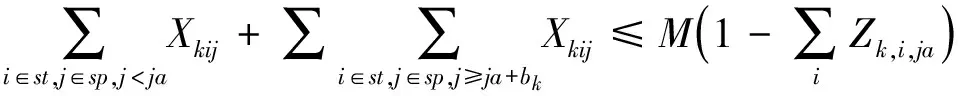
(25)

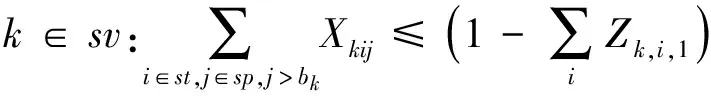
(26)

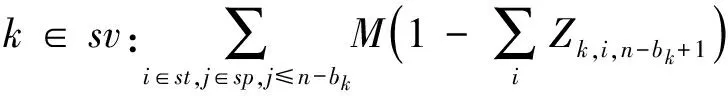
(27)

(28)

式(6)～式(9)规定了各项惩罚成本的惩罚量；式(10)表示船舶必须在达到后才能开始作业；式(11)规定了Ck与Vki的关系；式(12)保证一个网格最多只能被一条船占据；式(13)限制了各时间段可利用岸桥数；式(14)保证船舶作业所需的总岸桥时数；式(15)、式(16)规定了Vki与Yki的关系；式(17)、式(18)表示k船舶同时作业的最小和最大岸桥数；式(19)、式(20)规定了Vki与Xkij的关系；式(21)约束Vki的取值；式(22)、式(23)表示Vki与Zkij的所有关系；约束式(24)表示每条船舶只有一个靠泊位置和时间；约束式(25)～式(28)限制了二维坐标轴中Xkij的取值。

2.2.2 分层调整模型

此模型主要是在码头泊位-岸桥集成分派基础上，考虑因船舶延期时的分层调整方法，建立因靠泊位置、时间偏差产生的惩罚成本以及岸桥作业效率提高、岸桥数增加所产生的成本最小化的多目标模型。当进行调整时，备用岸桥数限制为m座，这些岸桥作业效率与原先岸桥一样，不能超负荷作业，增加的岸桥作业成本每单位时间增加Δc1单位成本。此外，当船舶延期而需要提高岸桥作业效率时，由于岸桥本身作业能力限制及同时作业岸桥数的影响，只能在原先作业岸桥效率基础上提高α，此时增加的成本为每岸桥每单位时间Δc2单位成本。需要调整的船舶和时间集合分别记为asv和ast。模型目标函数如式(29)～式(31)，其中，式(31)表示采取调整策略所增加的岸桥成本：

minimizef′=f(fc1,fc2,fc3,fc4)

(29)

f≥fc1+fc2+fc3+fc4

(30)

约束式(3)～式(5):

(31)

该模型约束条件除了包括约束式(6)～式(12)，式(19)～式(28)，还有以下约束：

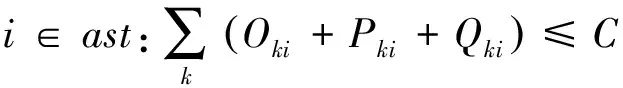
(32)

(33)

∀k∈asv,i∈ast:Oki+Pki+Qki≥Vki

(34)

∀k∈asv,i∈ast:Oki+Pki+Qki≤MVki

(35)

∀k∈asv,i∈ast:Oki+Pki+Qki+M(1-Vki)≥lk

(36)

∀k∈asv,i∈ast:Oki+Pki+Qki≤uk

(37)

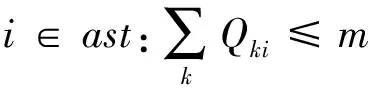
(38)

式(32)～式(37)是在式(13)～式(18)基础上考虑提高岸桥作业效率和增加岸桥数所满足的约束，式(38)表示时刻i的备用岸桥数最多为m座。

3 算例仿真

3.1 参数设置及初始分配调度方案

1)码头泊位总长度为1 200 m，以50 m为单位长度划分泊位轴，共分24个泊位格，将时间轴分为48 h。在此期间，将先后12条船舶靠泊此码头作业。

2)船舶预计达到时间ek由Excel随机生成区间[1，37]内的值；偏好靠泊位置rk取随机区间[1，18]；作业岸桥数ak取范围为[15，35]的数值。根据ak在ek取值基础上对应增加7～10得到预计离开时间dk，船舶长度bk本算例中以50 m为泊位单位长度，取值自区间[4，8]，根据实际中岸桥间距一般为80 m取相应的lk和uk值(表1)。

表1 算例数据

3)对每条船而言，各单位惩罚成本是一样的，取值为：c1k=1 000元，c2k=1 000元，c3k=2 000元。

4)最大可利用岸桥数C=12台，常数M=9 999。

5)在进行分层调整时，由于岸桥成本高昂，因此备用岸桥数m=1台，备用岸桥单位时间新增成本Δc1=150元，岸桥作业效率提高率α=0.2，岸桥作业效率提高单位时间新增成本Δc2=100元。

通过以上参数设置，采用CPLEX编程求解得到码头初始泊位-岸桥分配调度方案如图3。从图3中，可以直观看出每条船舶的靠泊位置和靠泊作业时间以及各时刻的作业岸桥数。该方案的目标函数值f=4 000元。

图3 初始泊位-岸桥分配调度方案Fig.3 Original schedule of berth-crane allocation plan

3.2 干扰调整分析

在初始方案的基础上，这里假设船舶9因突发事件而延期抵达。由于船舶8预计在16 h抵港靠泊作业，因此算例考虑船舶延期时间为1～7 h之间，以此来分析延期偏差程度的不同所采取的调整方案。分别采取分层调整策略和重调度策略进行计算分析，船舶9延期抵达，靠泊作业有可能受影响的船舶及其分层如表2。

表2 影响船舶分层

当船舶延误2 h以内时，通过岸桥的调整即可完成调整。当船舶9延误3 h时，通过简单计算可算出，需要调整的船舶集合asv={9,3,5,8}，时间集合ast={11,12, …,23}，应用分层调整模型计算得出船舶9延误3 h的调整方案如图4，其余船舶按原计划靠泊作业。

图4 船舶9延误3 h时的调整方案Fig.4 Adjustment solution of vessel 9 with 3 hours delay

在图4中，每个矩形上方的数值表示某时刻这些岸桥超负荷作业，下方数值表示这些岸桥正常作业，此时新增加的成本为2 000元。依次计算出船舶9延误1～7 h的调整方案及增加的成本，整理结果如表3。采取两种调整策略计算出来的一些指标如表4。

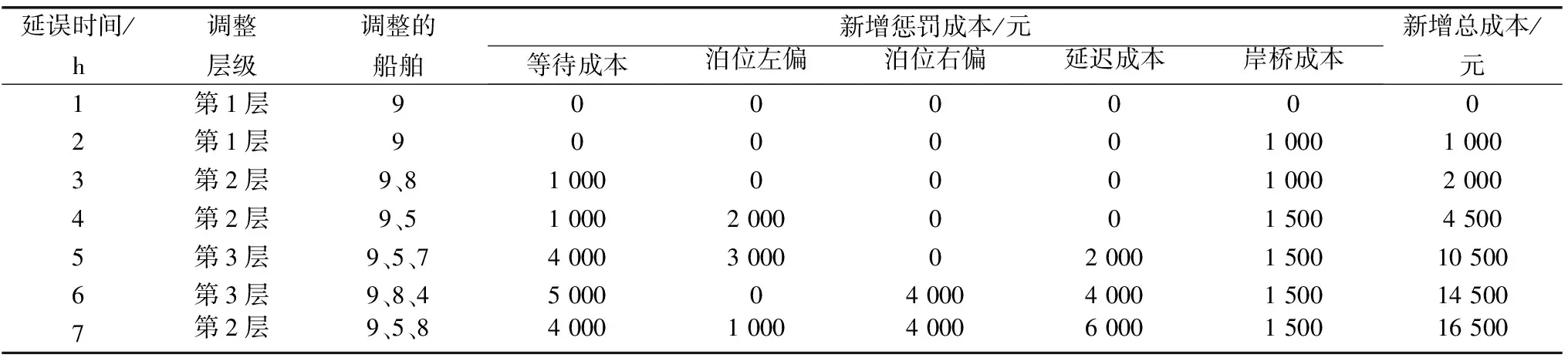
表3 船舶9延误时间不同情况下分层调整结果

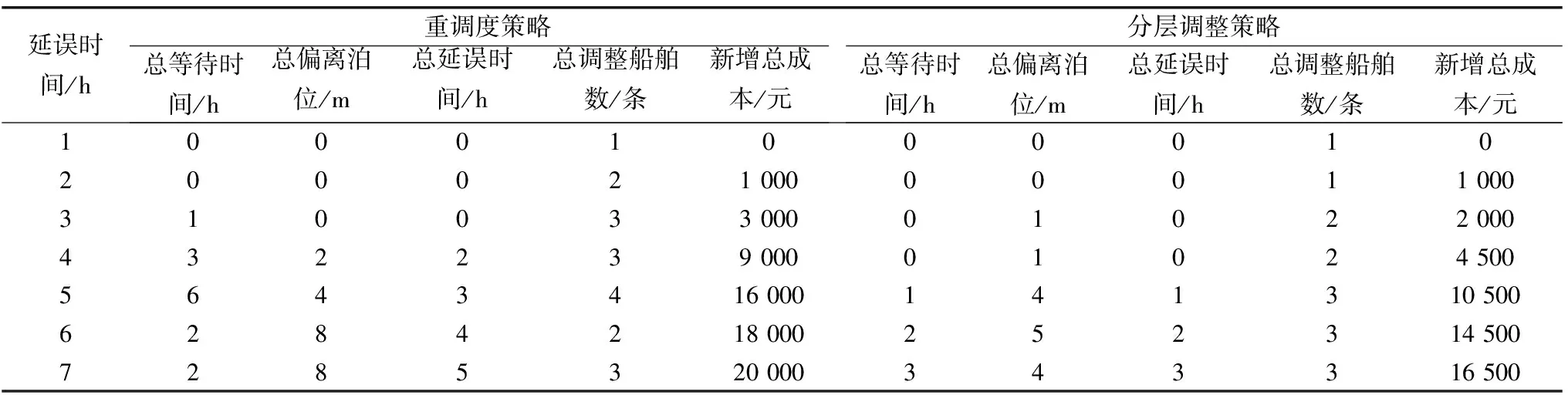
表4 两种调整策略的计算结果对比

从表3可以看出：

1)随着船舶延误时间越长，需要调整的层次越多，调整的船舶数也越多。此外，新增总成本也越多，并且随着调整层级的增多更加明显。

2)由表3 可以看出：当船舶延误时间较短时(如本算例中的2 h)，可以通过提高岸桥装卸效率让该船按期离港，保证之后船舶的正常靠泊作业。

3)当船舶延误时间较长时，对后面船舶靠泊作业时间影响较大，等待成本和延迟成本明显增加。

4)当延误时间超过4 h时，岸桥成本的增加趋于稳定，而泊位和时间的偏差带来的惩罚成本急剧增加，说明延期时间越长，影响数量多，这时岸桥调整能力虽然可以减少作业时间，但获得的方案对系统的干扰程度较大，造成的船舶延误时间较长。这种情况下，泊位调整是更好的选择，因此泊位偏差成本明显增加。

5)当船舶9延误时间为7 h时，调整的层级相对6 h时少了1层，说明延期时间过长，通过岸桥的调整带来的时间成本的增加比通过泊位的调整带来的成本增加高，因此可以采用调整泊挂靠泊位的方法，完成对干扰事件的调整。

由表4可知：

1)在船舶不同延期程度下，相对重调度策略，分层调整策略带来的新增成本更小，此外，船舶总的延误时间更短，泊位偏离更少，这样更有利于保障船方和货主的利益。

2)当船舶延期时间超过6h时，采取重调度策略下船舶总的等待时间明显降低，是由于船舶延期时间过长，可以考虑通过泊位的调整降低总成本。

4 结 语

以船舶在时间，靠泊位置等的偏差产生的惩罚成本最小化为目标，建立连续型泊位-岸桥集成分派混合整数规划模型，通过CPLEX求解出较为合理的泊位-岸桥分配调度方案。在此基础上，提出了一种通过泊位和岸桥调整的分层调整策略，用以对初始分配调度方案执行过程中的干扰事件进行有效处理。这种调整方法能够减少干扰事件的不可预测性产生的影响，既克服了扰动程度过大无法及时完成调整，也克服了重调度所带来的各方间接利益损害的缺陷，是一种较为合适的干扰管理调整策略。在算例中表明，相对于重调度策略，分层调整策略按层级进行调整，一定程度上提高了计算性能，降低了船舶的延误时间，同时增加的成本也比重调度策略更少，得到的应对方案更加合理。

[1] Yu G,Qi X T.Disruption Management: Framework,Models and Applications [M].Denmark: World Scientific, 2004.

[2] Clausen J,Larsen J,Larsen A,et al.Disruption management-operations research between planning and execution [J].OR-MS Today,2001, 28(5): 40-43.

[3] 胡祥培,张漪,丁秋雷,等.干扰管理模型及其算法的研究进展[J].系统工程理论与实践,2008,28(10):40-46.

Hu Xiangpei,Zhang Yi,Ding Qiulei,et al.Review on disruption management model and its algorithm [J].Systems Engineering-Theory & Practice, 2008, 28(10): 40-46.

[4] Evers P T.Filling customer orders from multiple locations:A comparison of pooling methods [J].Journal of Business Logistics, 1999, 20(1): 121-140.

[5] Hong-Minh S M,Disney S M,Naim M M.The dynamics of emergency transhipment supply chains [J].International Journal of Physical Distribution & Logistics Management, 2010, 30(9): 788-816.

[6] Love M,Sorensen K R,Larsen J,et al.Disruption management for an airline rescheduling of aircraft [J].Applications of Evolutionary Computing, 2002, 2279(3): 315-324.

[7] 王旭坪,许传磊,胡祥培.有顾客时间窗和发货量变化的车辆调度干扰管理研究[J].管理科学, 2008,21(5): 111-120.

Wang Xuping,Xu Chuanlei,Hu Xiangpei.Study on disruption management of vehicle routing problem with the changes of time windows and delivery weight of customers [J].Journal of Management Science,2008, 21(5):111-120.

[8] Lee C Y,Leung J Y T,Yu G.Two machine scheduling under disruptions with transportation considerations [J].Journal of Scheduling, 2006, 9(1): 35-48.

[9] Lewis B M,Erera A L,White C C.The impact of temporary seaport closures on freight supply chain costs [J].Journal of the Transportation Research Board, 2006, 1963(1): 64-70.

[10] Zhu G,Bard J F,Yu G.Disruption management for resource-constrained project scheduling [J].Journal of the Operational Research Society, 2005, 56(4): 365-381.

[11] Park Y M,Kim K H.A scheduling method for berth and quay cranes [J].Or Spectrum-Quantitative Approches in Management,2003, 25(1): 1-23.

[12] 韩晓龙,丁以中.集装箱港口泊位配置优化[J].系统工程理论方法应用,2006,15(3):275-278.

Han Xiaolong,Ding Yizhong.Optimization of berth allocation problem in container terminals [J].Systems Engineering: Theory Methodology Applications, 2006, 15(3): 275-278.

[13] Monoaca M F, Sammarra M.The berth allocation problem:a strong formulation solved by a lagrangian approach [J].Transportation Science, 2007, 41(2): 265-280.

[14] Legato P,Gulli D,Trunfio R.The quay crane deployment problem at a maritime container terminal [C/OL]// Proceedings of the 22ndEuropean Conference on Modeling and Simulation.Cyprus,Italy,June 3rd-6th,2008[2013-01-12].http:www.scs._europe.net/conf/ecms 2008/ecms 2008%20CD/ecms 2008%20pdf/ibs-ECMS 2008_0106.pdf.

[15] Giallombardo G,Moccia L,Salani M,et al.Modeling and solving the tactical berth allocation problem [J].Transportation Research Part B: Methodological, 2010, 44(2): 232-245.

[16] 周鹏飞,康海贵.面向随机环境的集装箱码头泊位-岸桥分配方法[J].系统工程理论与实践,2008(1):161-169.

Zhou Pengfei,Kang Haigui.Study on berth quay-crane allocation under stochastic environments in container terminal [J].Systems Engineering-Theory & Practice, 2008(1):161-169.

[17] 曾庆成,胡祥培,杨忠振.集装箱码头泊位分配-装卸桥调度干扰管理模型[J].系统工程与理论实践,2010,35(11):2026-2035.

Zeng Qingcheng,Hu Xiangpei,Yang Zhongzhen.Model for disruption management of berth allocation and quay crane scheduling in container terminals [J].Systems Engineering-Theory & Practice,2010, 35(11): 2026-2035.

[18] 杨春霞,王诺.集装箱码头泊位分配干扰管理模型决策方法研究[J].运筹与管理,2011,20(4):90-95.

Yang Chunxia,Wang Nuo.Decision-making method for berth allocation disruption management in container terminal [J].Operations Research and Management Science, 2011, 20(4): 90-95.

[19] Imai A,Chen H C,Nishimura E,et al.The simultaneous berth and quay crane allocation problem [J].Transportation Research Part E: Logistics and Transportation Review, 2008, 44(5): 900-920.

[20] Liang C,Huang Y,Yang Y.A quay crane dynamic scheduling problem by hybrid evolutionary algorithm for berth allocation planning [J].Computers & Industrial Engineering,2009,56(3): 1021-1028.

[21] Lee D H,Wang H Q.Integrated discrete berth allocation and quay crane scheduling in port container terminals [J].Engineering Optimization, 2010, 42(8): 747-761.

[22] Zhou P,Kang H.Study on berth and quay-crane allocation under stochastic environments in container terminal [J].Systems Engineering-Theory & Practice, 2008, 28(1): 161-169.

[23] Raa B,Dullaert W,Schaeren R V.An enriched model for the integrated berth allocation and quay crane assignment problem [J].Expert Systems with Applications, 2011, 38(11): 14136-14147.

[24] Zhang C, Zheng L,Zhang Z, et al.The allocation of berths and quay cranes by using a sub-gradient optimization technique [J].Computers & Industrial Engineering, 2010, 58(1): 40-50.

[25] Chang D,Jiang Z,Yan W,et al.Integrating berth allocation and quay crane assignments [J].Transportation Research Part E:Logistics and Transportation Review, 2010, 46(6): 975-990.