潜射导弹筒口气泡发展规律研究
邱海强,袁绪龙,王亚东,刘传龙
(西北工业大学 航海学院,陕西 西安710072)
0 引言
不带运载器的垂直无动力燃气-蒸汽弹射是潜射导弹的一种常见发射方式。导弹发动机不点火,靠发射装置附带的燃气-蒸汽发生装置产生气体来推动导弹加速出筒;导弹被弹射出筒后,依靠自身出筒速度出水,在离开水面后点火。由于弹尾和发射筒口之间的间隙,混合气体从其中溢出,不但对导弹的运动产生影响,而且其产生的压力脉动可能会影响发射平台。
对于筒口气泡的发展过程,李杰等[1]利用Rayleigh-Plesset 方程建立了等压球状尾泡模型来研究燃气后效,提供了研究该问题的一种思路;但根据刘志勇等[2]的采用BUBMAC 算法[3]得到的研究结论,筒口气泡在水压和弹体运动影响下会拉断为两个气泡,等压球状尾泡模型的运用只能近似描述气泡拉断前气泡的发展情况;王亚东等[4]利用计算流体力学(CFD)软件Fluent 对整个弹射过程进行了研究,着重分析了伴随气泡发展而产生的压力脉动情况,得到了与试验数据吻合良好的仿真结果。另外,曹嘉怡等[5]采用有限体积法对导弹无动力出筒过程尾部水气流场进行了数值模拟;王汉平等[6]针对潜射模拟弹筒口压力场进行了仿真计算,着重研究了筒盖载荷。
本文利用商业CFD 软件Fluent 研究了MIXTURE 模型下筒口气泡的发展规律,探讨了气泡内部不同位置的压力变化规律和压力传递过程,通过比较不同时刻泡内压力、气泡形态和导弹运动情况分析了三者在筒口气泡的发展过程中的耦合关系,仿真方法和结果可用于工程预报。
1 模型建立
1.1 影响分析与模型简化
筒口气泡并不是一个自由发展的气泡,其形态演变往往受限于筒口、发射平台壁面和弹尾之间形成的有限空间。所以在导弹弹射出筒的过程中,影响筒口气泡的因素主要有3 个方面:发射平台的结构特点、导弹的结构和运动、弹射气体的状态。
为了简化计算,忽略因潜艇运动而产生的侧向横流,这样导弹就简化为一维运动,采用三维模型进行计算;不考虑发射筒内的具体结构和筒盖打开后对筒外流场的影响;忽略导弹的头部形状,因为水下弹射的时间较短,忽略肩部空泡和发射筒的传热损失,只考虑弹尾结构对筒口气泡的影响;弹射气体用理想气体代替,其参数按实际弹射气体的组分进行折算;计算起点为弹尾离筒时刻,并对弹射气体做均匀静止假设。
1.2 计算区域和网格划分
建立如图1所示的计算区域,外场区域为20 m×24 m×12 m,并依据以下要点划分网格:1)导弹在轴向的运动是自始至终的,所以对轴向的网格要采用足够细密的均匀布置,使得仿真计算具有网格无关性;2)弹尾采用非结构网格来适应其外形,其余区域采用结构化网格,并做到近场细密,远场相对稀疏;3)因为采用了动网格技术,在interface 两侧要注意网格的连贯性,实现平滑过渡,以免影响气泡在其两侧的自由发展,必要时可以根据密度对气液交界面进行网格加密。最终采用的经过网格无关性验证的网格量大约为142 万。
1.3 计算设置
采用如下计算设置:
1)多相流模型采用MIXTURE 模型,湍流模型采用RNG k-ε 模型,压力速度耦合方式采用PISO;
2)因为垂直发射的缘故,需要在x 轴负向给定重力加速度,弹体离筒速度为36.26 m/s;
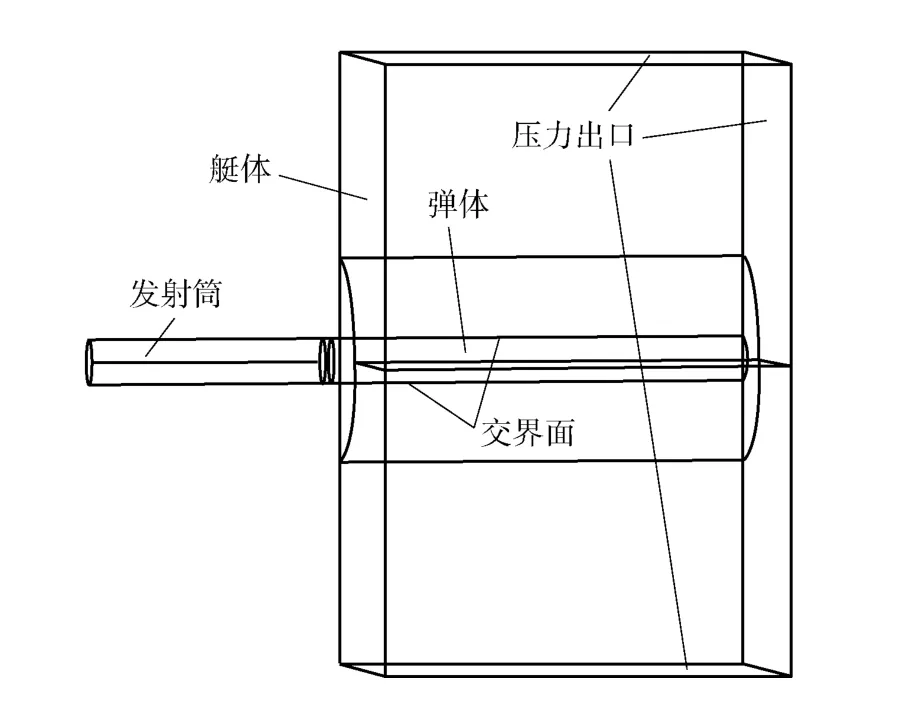
图1 计算区域划分Fig.1 Computational domain
3)弹体的运动状态通过UDF 根据流场情况计算得出,其初始状态的计算依据是导弹尾部离开发射筒时混合气体的余压0.72 MPa、余温422 K 和筒外海水的状态,并按发射水深20 m 给定压力梯度。
2 计算结果分析
2.1 筒口气泡的发展历程
初始时刻发射筒内全部为混合气体,发射筒外全部为水;弹尾离开发射筒后,混合气体从弹尾和发射筒的间隙中迅速溢出,筒口气泡不断发展,形成了一个闭合于弹尾的类半球形气泡,该过程海水体积分数图如图2所示。
如图3所示,随着气泡的不断膨胀,混合气体的压力和温度迅速下降,气泡的膨胀速度会逐渐减小,当膨胀速度小于导弹的运动速度时,导弹的抽吸作用使得附着在气泡部分继续跟着导弹运动,靠近筒口处的气泡部分此时受到静水压力而逐渐变小;压力进一步降低后,气泡无法承受外界压力,从气泡中部最细的部位开始分成两个独立的气泡:弹尾气泡和筒口气泡。
气泡拉断后,在拉断处形成一个高压区,进一步影响气泡的变化。弹尾气泡尺度变小,气泡由于表面张力作用剖面形状趋于半椭圆形;筒口气泡在水压作用下尺度变小且水在发射筒边缘位置灌入发射筒。在这个过程中,水-气界面变得愈加模糊,水-气交互作用越来越强烈,水-气掺混程度加大。此阶段海水体积分数如图4所示。

图2 t=0.04 s,0.08 s,0.12 s,0.16 s 时刻海水体积分数Fig.2 Contour of phases at t=0.04 s,0.08 s,0.12 s,0.16 s
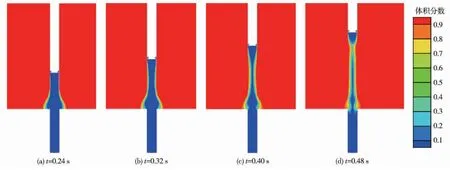
图3 t=0.24 s,0.32 s,0.40 s,0.48 s 时刻海水体积分数Fig.3 Contour of phases at t=0.24 s,0.32 s,0.40 s,0.48 s
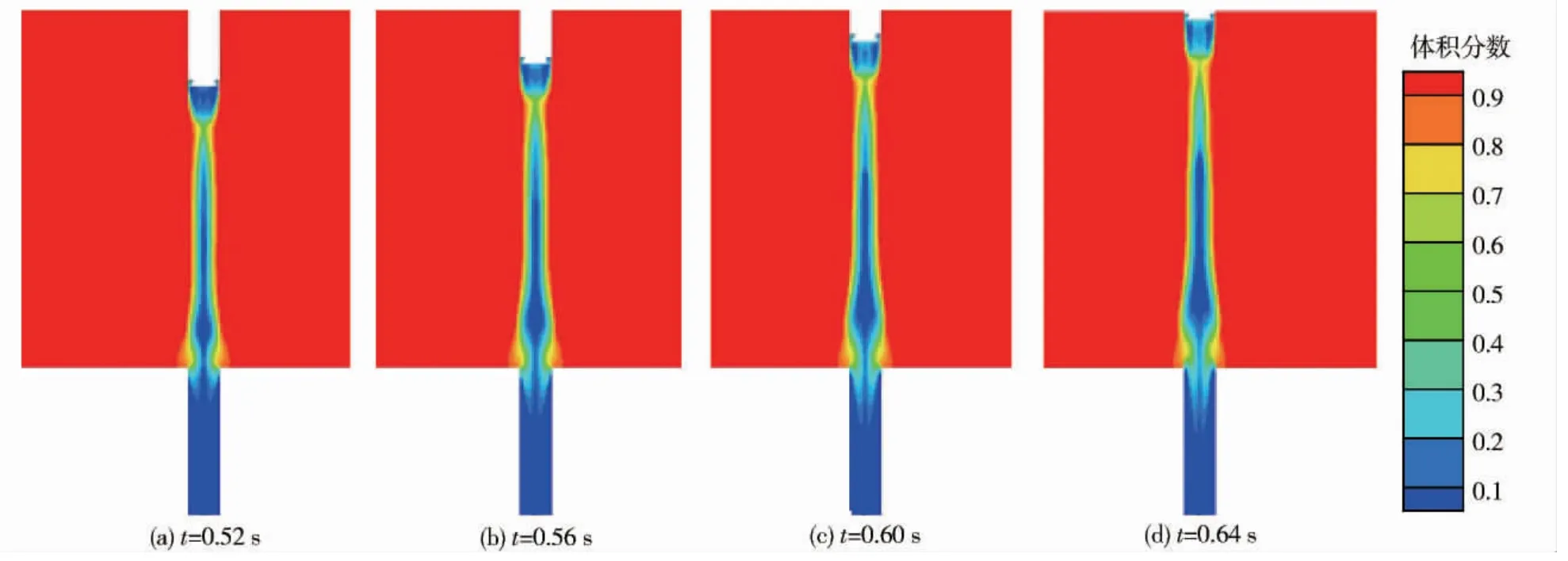
图4 t=0.52 s,0.56 s,0.60 s,0.64 s 时刻海水体积分数Fig.4 Contour of phases at t=0.52 s,0.56 s,0.60 s,0.64 s
以气液界面上混合气体的体积分数等于0.5 为标准提取气泡轮廓,并对不同时刻气泡的形态进行对比,如图5所示。从图5可以看出,一开始近艇体处的气泡处于急速扩张阶段,附着在弹尾的气泡被拉伸,其气泡最大直径与弹径相同;气泡扩大到一定程度后,近艇体处的气泡开始被压缩,气泡中部被海水挤压,开始渐渐的收缩,这也影响了弹尾气泡的形态;随着海水倒灌现象的发生,近艇体处的气泡被海水侵占,筒内气体溢出,在离筒口不远处形成一个较大的气泡,整个筒口气泡被拉断成两个气泡,弹尾气泡形态也受到了海水压缩的作用。
2.2 导弹运动状态

图5 不同时刻气泡形态Fig.5 Shapes of cavity at different times
导弹的运动状态也影响着气泡的发展情况,如图6所示。由于弹尾离筒之后,作用在弹尾的混合气体压力较高,相当于提供了导弹运动的一个很大的“推力”,导弹加速运动,但筒口急剧的泄压作用,导弹的加速度逐渐减小;随着筒内气体不断溢出,在极短的时间里补充到弹尾,使得此时气泡压力保持一定程度上的稳定;气泡继续膨胀,与外界的热传递造成的能量损失使得附着在弹尾的气泡压力下降,其运动加速度开始下降;气泡中部开始拉断后,后部燃气往前输送的通道受限,附着在弹尾的气泡压力较低,当由于压差产生的“推力”与浮力之和小于其受到的阻力和重力之和时,加速度变为负值,导弹运动速度开始下降,由于拉断后弹尾气泡内压力变化幅度较小,所以其速度下降的较慢。
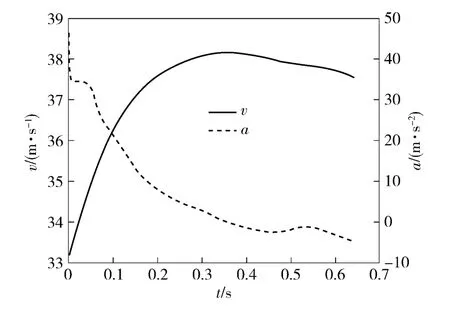
图6 导弹的运动参数Fig.6 Motion parameters of missile
2.3 泡内压力变化
筒口气泡内部的压力分布并不是均匀分布的,而且在出筒后期气泡一分为二,泡内压力的变化就更为复杂,不妨取筒口中心处压力p0和弹尾中心处压力p1来分析气泡拉断之后泡内压力的变化。起初,筒口和弹尾压力保持相同的变化趋势,随着气泡形态的变化过程中的能量损失,压力急剧下降;气泡中部开始拉断时,在拉断处形成一个高压区,因此形成冲击弹尾和发射筒的两股射流,使得弹尾和筒口两处压力产生脉动。
由图7可知,冲击弹尾的射流很快就消散了,但是筒口处的射流引起的压力脉动确是持续的。在发射筒的中轴线上从筒口到筒底均匀布置13 个压力测点,观察发射筒内混合气体的压力变化规律。
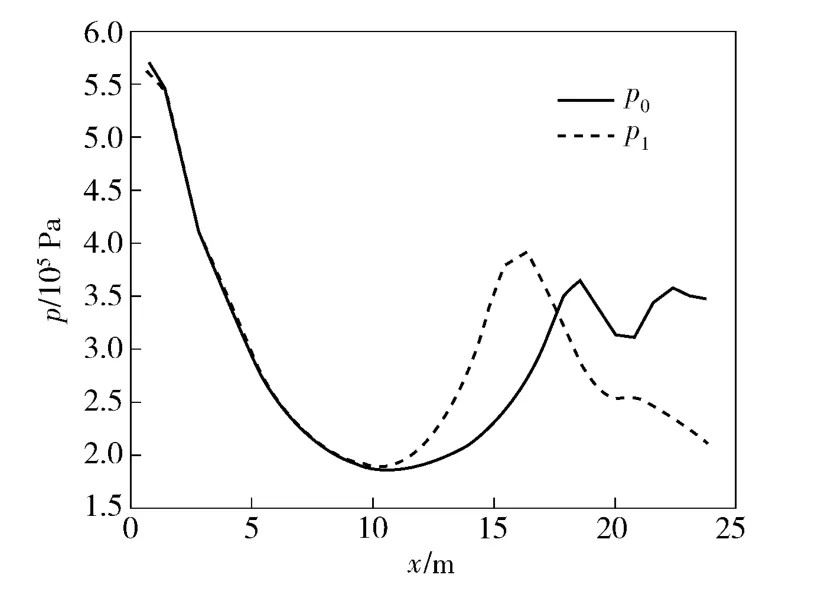
图7 不同位置压力变化Fig.7 Pressures in different positions
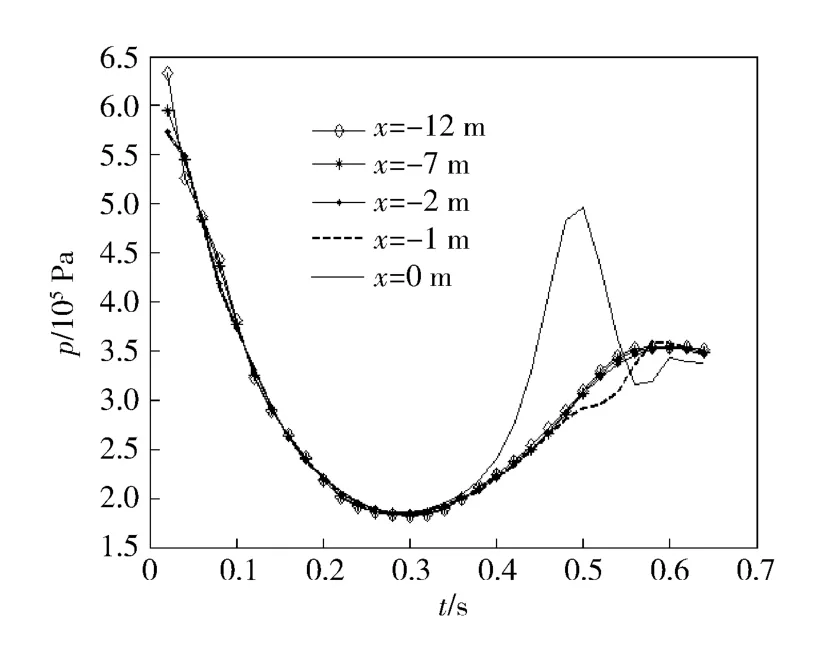
图8 不同位置时压力随时间变化Fig.8 Pressures in different positions
由图8可见,出筒后的极短时间里,筒口压力下降的较快,筒内压力下降的较慢;筒口气泡对筒内压力的影响主要集中在筒口部分,对筒内的影响很小。从图8中可见,同一时刻不同位置的压力值并不相同,这是因为筒口到筒底之间存在着压力脉动,压力总是从压力较大的点传递到压力较低的点。不妨以x=0 m 处压力的次峰值发生之后筒内压力的脉动过程来描述这一过程。当t=0.50 s 时x =0 m 处出现了一个次峰值,此时此处的压力比筒内各点的压力大很多,压力开始向内传递;如图9所示,从t =0.50 s 时开始,近筒口处压力不断下降,远离筒口处的压力不断上升,并且压力下降的幅度比上升的幅度大得多,这样的好处是在发射过程中不要担心压力传播对发射筒乃至于艇体造成破坏。

图9 压力传递过程Fig.9 Transmission process of pressure
2.4 泡内压力与气泡尺寸的关系
采用气泡在纵向位置上的最大尺寸和筒口中心的压力来描述气泡形态与泡内压力演化规律,如图10所示。
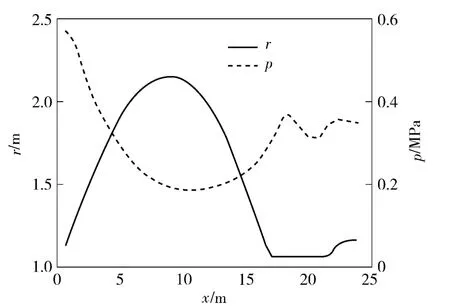
图10 气泡形态和压力变化的关系Fig.10 Cavity shape and pressure
出筒伊始,泡内压力急剧下降,气泡沿着艇体表面急剧向外扩散,气泡最大尺寸出现在近艇体处,所以气泡尺寸跟着迅速变大,此时附着在弹尾的气泡尺寸与弹径相同;当气泡膨胀到一定大小之后,泡内压力达到极小值,气泡受到水压作用,开始收缩,泡内压力又开始逐渐变大;气泡拉断之后,如图5中t=0.52 s 所示,近艇体处气泡被海水严重压缩,筒口气泡的最大尺寸小于附着在弹尾的气泡尺寸,此时气泡的最大尺寸出现在弹尾处,并保持一定时间;随着海水倒灌现象的发生,气体从发射筒沿着筒的中部溢出,在距离艇体不远处,形成了一个较大的气泡,如图5中t =0.62 s 所示,气泡的最大尺寸形成于该处,并且随着海水倒灌的加剧继续变大。
3 结论
本文利用MIXTURE 模型对导弹尾部离筒后,筒口气泡的发展情况进行了CFD 分析,得到了如下结论:
1)导弹出筒之后,筒口气泡在其内部压力温度、弹体运动和发射平台影响下经历了扩张、收缩、拉断等一系列过程,最终形成了海水倒灌。
2)导弹出筒之后先做加速度不断减小的变加速运动,气泡拉断后弹体运动加速度开始降低直至变为负值,速度开始降低。
3)气泡内部压力因气泡形态变化导致的射流而产生脉动现象,发射筒内的压力传递现象比较平缓,对发射筒内的结构安全影响较小。
4)气泡形态变化与其所处位置的压力变化呈明显的负相关关系。
References)
[1] 李杰,鲁传敬. 潜射导弹尾部燃气后效建模及数值模拟[J].弹道学报,2009,21(4):6 -8.LI Jie,LU Chuan-jing. The model of combustion gas bubble of submarine-launched missile and numerical simulation[J]. Journal of Ballistic,2009,21(4):6 -8. (in Chinese)
[2] 刘志勇,颜开,王宝寿. 潜射导弹尾空泡从生成到拉断过程的数值模拟[J]. 船舶力学,2005,9(1):43 -50.LIU Zhi-yong,YAN Kai,WANG Bao-shou. Numerical simulation of the development process of a trailing cavity from generation to separation[J]. Journal of Ship Mechanics,2005,9(1):43 -50.(in Chinese)
[3] Yan K. The BUBMAC method—a numerical method bubble dynamics in vortex core[J]. Journal of Hydrodynamics:Ser B.1998,10(3):1 -16.
[4] 王亚东,袁绪龙,覃东升. 导弹水下发射筒口气泡特性研究[J]. 兵工学报,2011,32(8):991 -995.WANG Ya-dong,YUAN Xu-long,QIN Dong-sheng. Research of the outlet cavity features during the launch of submarine launched missile[J]. Acta Armamentarii,2011,32(8):991 -995. (in Chinese)
[5] 王汉平,余文辉,魏建峰. 潜射模拟弹筒口压力场仿真[J]. 兵工学报,2009,30(8):1009 -1013.WANG Han-ping,YU Wen-hui,WEI Jian-feng. Simulation of pressure field near canister outlet for underwater-launched emulated missile[J]. Acta Armamentarii,2009,30(8):1009 -1013.(in Chinese)
[6] 曹嘉怡,鲁传敬,李杰,等. 潜射导弹水下垂直自抛发射过程研究[J]. 水动力学研究与进展,2006,21(6):752 -758.CAO Jia-yi,LU Chuan-jing,LI Jie,et al. Research on the vertical launching of direct igniting underwater missile[J]. Journal of Hydrodynamics,2006,21(6):752 -758. (in Chinese)

