从数学的本质探东西方数学教育的差异

吴道春

1东西方对数学本质的认知差异

数学家们一般认为： 数学的本质是经验性和演绎性的辩证统一. 数学源于生活，如计算时间、分配物品、丈量土地和容积等，所以19世纪之前，人们一般认为数学是一门经验科学. 19世纪以来，随着近现代数学的不断发展，特别是欧式几何、非欧几何、抽象代数和集合论等的产生，现代数学向抽象、多元、高维发展，人们的注意力集中到这些抽象对象上，数学与现实之间的距离渐渐远去，数学在数学研究中占据了重要地位，人们越来越认为数学是一门演绎科学. 1931年，歌德尔不完全性定理的证明宣告公理化逻辑演绎系统存在缺憾，匈牙利著名数学哲学家拉卡托斯对数学的经验性和演绎性作出概括，认为数学具有拟经验性. 当代计算机技术的高速发展，人们可以用计算机进行数值计算.数学实验和机器证明，实现了经验性和演绎性的新的融合和统一.

近现代，数学在西方科技、经济等领域的发展中得到广泛应用，数学的应用价值逐渐被人们重视，形成和发展了一个新的数学分支——应用数学，西方的数学教育也走向了重实用和经验的道路；中国的数学教育受苏联的影响很大，在八九十年代走上了与中国数学传统相反，追求严密化、形式化的道路，侧重数学的演绎性. 对数学本质的不同侧重，是东西方在数学教育理念、数学课程目标、数学课程内容、教材结构体系、课堂教学方式、概念理解、技能训练、问题解决、数学探究和综合难度等方面存在差异的根源.

2东西方数学教育的差异

2.1数学教育理念

我国的数学教育侧重数学的演绎性，所以，一直以来我们特别强调“双基”教学，只有学生的“双基”扎实了，他们才能够发展较高水平的演绎推理能力；教材、教辅和考试试卷中有很多题难度水平比较高，设置这些难题的主要目的就是要培养和考查学生的演绎推理能力. 美英等国的数学教育侧重数学的经验性，鼓励学生试验、观察、操作、发现、探究、交流、创造，重视培养学生的动手和创造能力. 因此，我国学生的数学基础知识较扎实，解题水平较高，而动手和创造能力就不如美英国家.

2.2数学课程目标

我国普通高中数学课程标准（实验）确定的数学课程目标是：（1） 获得必要的数学基础知识和基本技能，理解基本的数学概念、数学结论的本质，了解概念、结论等产生的背景、应用，体会其中所蕴涵的数学思想和方法，以及它们在后续学习中的作用. 通过不同形式的自主学习、探究活动，体验数学发现和创造的历程；（2）提高空间想像、抽象概括、推理论证、运算求解、数据处理等基本能力；（3）提高数学地提出、分析和解决问题（包括简单的实际问题）的能力，数学表达和交流的能力，发展独立获取数学知识的能力；（4）发展数学应用意识和创新意识，力求对现实世界中蕴涵的一些数学模式进行思考和作出判断；（5）提高学习数学的兴趣，树立学好数学的信心，形成锲而不舍的钻研精神和科学态度；（6）具有一定的数学视野，逐步认识数学的科学价值、应用价值和文化价值，形成批判性的思维习惯，崇尚数学的理性精神，体会数学的美学意义，从而进一步树立辩证唯物主义和历史唯物主义世界观.

美国课程标准（2000版）中这样叙述：我们的数学课程必须联系我们的学生的兴趣；聚焦数学的逻辑与实验特征；为数学学习创设丰富的环境；了解学生的数学体验. 英国2000年国家数学课程的三大目标：让大多数人掌握“基本技能”；为少数人传授一定的符号操作和运算的知识；培养“现实生活”应用所需的技能.

可以看出，我国数学课程的目标首先是使学生获得必需的基本知识和基本技能，在此基础上培养学生的数学思维能力，让学生体验数学的价值，具有数学应用意识. 美国数学课程强调联系学生的兴趣，为学生的实验、操作和体验创设环境. 我们的课程目标倾向于“建立在双基和思维基础上的体验和应用”，而美国的课程目标倾向于“建立在实验和操作基础上的双基和思维”. 英国的课程目标强调数学的实用性.

2.3数学课程内容

我国的数学课程（以苏教版教材为例）必修部分包括：集合、函数概念与基本初等函数Ⅰ（指数函数、对数函数、幂函数）；立体几何初步、平面解析几何初步；算法初步、统计、概率；基本初等函数Ⅱ（三角函数）、平面上的向量、三角恒等变换；解三角形、数列、不等式. 选修部分包括：常用逻辑用语、圆锥曲线与方程、导数及其应用；推理与证明、数系扩充与复数的引入、框图；空间中的向量与立体几何；计数原理、统计案例、概率.

美国在《标准（2000）》中为每个学段设立的数学课程内容包括：数与运算、代数、几何、测量、数据分析与概率、问题解决、推理与证明、交流、关联、表达.

2000年英国国家数学课程的教学内容包括：数与代数（使用和应用数与代数，数与数系，计算，解数的问题，处理、表示和解释数据，方程、公式和恒等式，数列、函数和图像）；形状、空间和测量（使用和应用形状、空间和测量，理解形状的模式和性质，理解位置和运动的性质，理解测量，几何推理，变换与坐标，测量与作图）；数据处理（使用和应用数据，明确问题和制定计划，收集数据，处理表示和解释数据，解释和讨论结果）.

我国的数学课程内容集中在数学的基础知识、基本技能和逻辑推理上，讲究学科内容覆盖的全面、层层递进和知识体系的完备，这是培养学生的演绎推理能力的内在要求. 美国和英国的数学课程内容联系实际生活经验，注重实用性，建立在学生的实验与操作的基础之上，要求学生进行数学表征、数学交流、数学应用和问题解决.

2.4教材结构体系

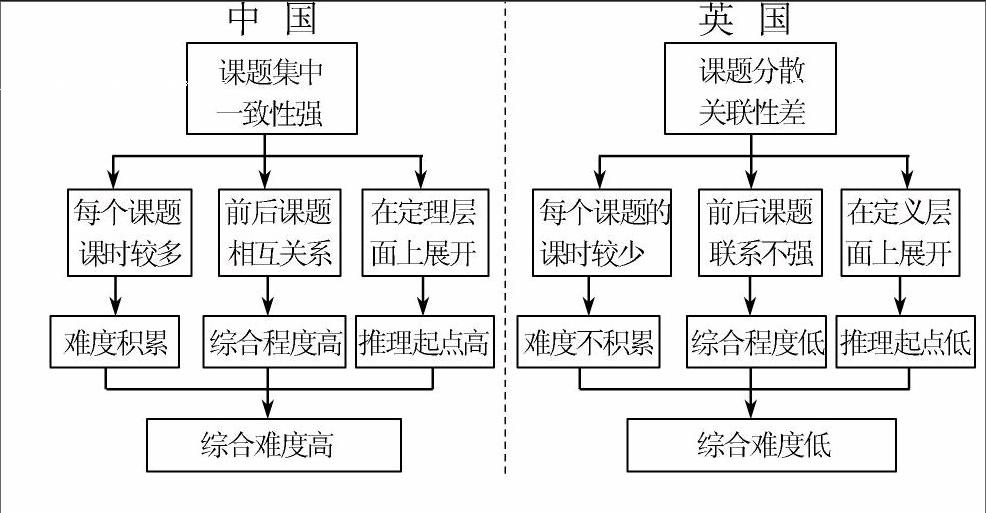
我们以中英两国的数学教材的结构体系（见上图）为例，我国的数学教材（苏教版）每个课题的课时较多，前后联系，由定理、公理构成演绎体系，综合难度高. 英国的数学教材（EXTER 大学“数学教学改革中心”的MEP 试验教材.）侧重数学的实用性和经验性，每个课题的课时较少，联系不强，不深挖掘，综合难度低.endprint

2.5课堂教学方式

在一节典型的中国数学课堂上，教师根据自己对课堂的精心设计有条不紊地讲解概念和例题，学生全神贯注地听讲，理解概念，根据教师的示范和要求进行解题训练，讲究一题多变、一题多解，即我们通常所说的“变式教学”，学生在“变与不变”中加深对概念的理解，强化对知识点之间的联系的认识以及对方法、技巧的掌握等，从而他们的演绎推理能力不断提高.

在一节典型的日本数学课堂上，教师通常出示一个复杂的问题，要求学生独立地寻求各种不同的解法，然后进行小组讨论， 接着由教师和学生一起对各种解法的优缺点进行分析，这样做的目的提高学生的演绎推理和问题解决能力.

在一节典型的美国数学课堂上，常常由教师先给出实验和操作的要求，然后学生进行操作、实验、探究和交流，或者教师给出某类问题的解法，然后学生练习一批类似的问题，整个课堂集中于学生通过实验达到对事实和程序的掌握.

2.6关于概念理解

我国的数学课程力求从原理的角度来描述和分析数学概念，证明相关定理、性质、公式和结论，使学生在理解的基础上获得概念. 英国的学生在老师的指导下完成操作，观察模式，归纳出相关概念，但这只是归纳，学生并不知道为什么. 英国学生的概念理解侧重于对事实和程序的记忆，而我国学生一般需要理解概念的内涵和外延. 这一差异也是由两国对数学的经验性和演绎性的不同侧重决定的.

2.7关于技能训练

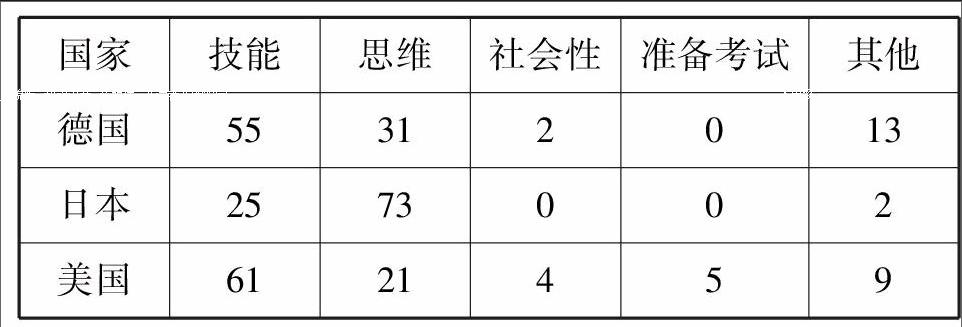
看一个关于教师对数学教学目标的看法的国际性的调查问卷，问题是：“你希望学生在这堂课主要学到什么东西？”统计结果见下表：

美国和德国教师重视数学技能，而日本教师重视数学思维， 有理由相信如果将中国教师纳入调查对象，结果也会与日本相似. 这与东西方对数学本质的不同侧重有着直接的关系.

一般认为数学技能包含两种：操作性技能和认知性技能. 操作性数学技能是指在头脑外部通过肌体活动来实现的动作，其活动对象是物质化的客体，是一种外显活动. 认知性数学技能是指头脑中的数学智力活动，其活动对象不是具有一定物质形式的客体，而是这种客体在头脑中的映象，因而是一种观念性的活动. 西方侧重数学的经验性，聚焦操作性数学技能，如使用计算工具（计算机等）、统计、测量、作图等，我国比较侧重数学的演绎性，聚焦认知性数学技能，如运算，式的恒等变换，解不等式，推理论证等.

2.8关于问题解决

中国数学课程中的问题解决具有以下特征：一般没有实际背景；涉及连续的、环环相扣的数学推理；需要学生主动地挖掘隐含的信息；知识的综合程度高，要求学生主动建立概念、命题之间的联系；可以分解为一系列的基本命题的组合，也可以通过局部调整产生各种新的变式题，因此题型的积累与相应的解题经验非常重要；技巧性高，要求解题者熟练掌握双基，从而把注意力集中在寻找解题策略上；需要较长的解题时间，高度集中的注意力，较强的意志力和较高的自信心；对智力是一个挑战，绝大多数解题者都会遇到各种困难，许多人会遭受失败；一旦获解，则会产生极大的满足感；背景简单、清晰，一般不需要运用日常生活的实际经验.

英国数学课程中的问题解决具有以下特征：通常具有实际或具体的背景；一般不涉及推理，或者只要求一步推理；题目中一般都包含有解题所需的全部信息，很少要求学生自己去挖掘除基本概念以外的隐含条件；一道题目一般只涉及单个知识点，较少要求学生去建立不同概念之间的联系；不必担心会因为信息的繁杂而顾此失彼；不同的题目之间缺少联系，很少出现相互组合、或者相互化归的情形；题型的积累与解题的经验并不重要；解题进程通常是单一方向的，即从条件到结论； 一般都有现成的解题程序，学生很少面临解题思路的抉择与调整；一般只需要几分钟就能解决问题；不同水平的学生通常有不同的要求，因此，绝大多数学生都不会遇到太多的解题障碍；背景的复杂性常常超过数学本身的复杂性.

总的来说，数学本身正以前所未有的“纯数学与应用数学，逻辑演绎与实验归纳”相统一的方向发展. 这表明，数学教育改革也应顺应时代的发展，在“两极”之间寻求最佳的动态平衡.endprint