基于灵敏度方法的车门模态优化

朱茂桃，陈亚洲

(江苏大学 汽车与交通工程学院, 江苏 镇江212013 )

车门一般由车门外板、车门内板、车门加强板、抗侧撞梁、车门附件等组件构成。作为轿车重要组成部分，车门不仅要满足刚度、强度要求，还要满足一定的模态特性。如果车门固有频率与白车身固有频率相近，很有可能会发生共振现象，极大地影响车辆的乘坐舒适性[1-2]。

为提高车身NVH性能，必须对车门模态进行优化，以避开白车身固有频率。基于此，国内学者做了相关方面的研究。姜连勃，等[1]主要说明了车门类型、各部件的功能以及车门布置形式，但是没有说明如何实现车门优化。王宏雁，等[2]通过研究车门不同材料不同结构的静动态性能，确定优化方案，但这种优化依赖于材料与焊接工艺。曹文钢，等[3]和石琴，等[4]主要研究灵敏度分析在车身优化方面的应用，通过灵敏度分析实现车身优化，证明了基于灵敏度分析优化的可行性。肖成林，等[5]主要利用拓扑与形貌的组合分析，提高车门刚度，减轻车门质量。雷明准，等[6]研究了车门模态特性并进行优化，但是以所有部件厚度作为设计变量，计算量较大。

因此，笔者对某车门进行计算模态分析，并通过模态实验验证。根据车门各部件灵敏度分析，判断影响车门模态的关键部件。最后，对关键部件进行尺寸优化，提高车门模态性能。

1 车门模态灵敏度分析基本理论

对于多自由度系统而言，可以运用达朗贝尔原理，建立如下系统运动微分方程：

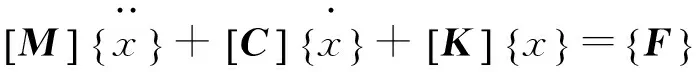
(1)

在无阻尼自由振动中，即不考虑阻尼和激励影响的情况下，假设ωi，{ui}分别为第i阶固有频率和振型向量，则必然满足特征方程式[3]：

(2)

结构性能参数对设计参数的灵敏度可以通过对设计参数偏导计算获得[4]。因此，笔者为获得车门固有频率对设计参数的灵敏度，在式(2)中两端同时对设计变量xj求偏导数，得到式(3)：

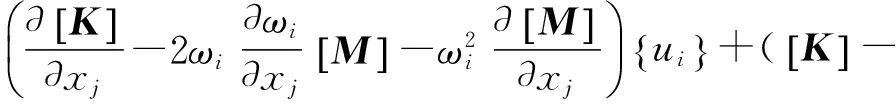
(3)

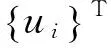
(4)

整理式(4)，即得到设计变量ωi对xj阶频率的灵敏度表达式(5)：

(5)

2 车门计算模态分析

2.1 车门有限元模型建立

车门部件主要是由厚度不足2 mm的薄板冲压焊接形成，其长度方向的尺寸远远大于厚度方向的尺寸，符合壳单元的理论假设。因此主要壳单元进行离散化[5]，网格大小为10 mm。

车门连接方式有：螺栓连接、包边、点焊、胶黏等。在有限元模型中，外板、内板包边工艺采用Rigid刚性单元模拟，点焊用Cweld单元模拟，胶黏采用Rigid刚性单元和Solid实体单元组合进行模拟[7]。

建立有限元模型如图1。车门节点总数为27 758，共生成26 428个壳单元。其中四边形单元总数为24 941，三角形单元总数为637，六面体单元总数为42，点焊单元146。

图1 车门有限元模型Fig.1 FEA model of car door

2.2 计算模态分析结果

通过OptiStruct求解器，进行自由模态分析。前5阶计算结果如表1、模态振型如图2。

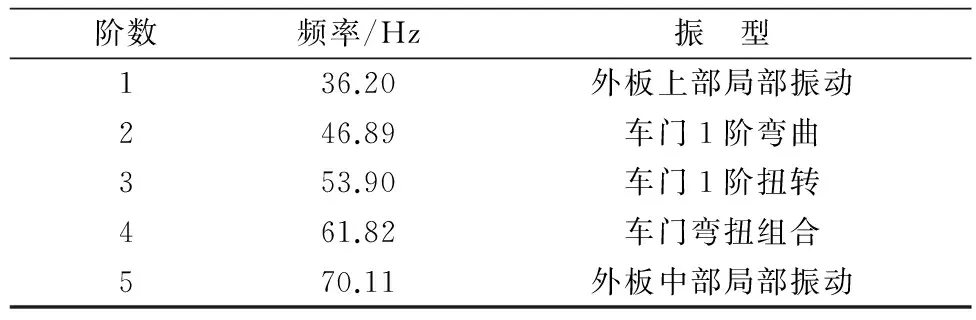
表1 车门计算模态结果 Table 1 Modal calculation results of car door

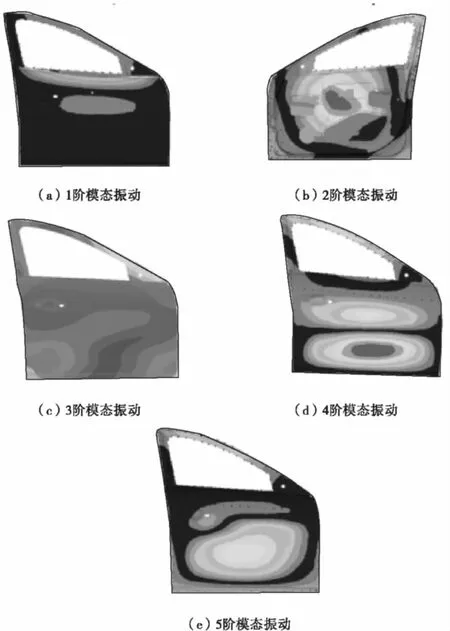
图2 1～5阶模态振型Fig.2 1～5order vibration mode

1阶固有频率为36.2 Hz，表现为车门外板的上部分的局部振动；2阶固有频率为46.89 Hz，表现为车门整体的1阶弯曲振动，其中内板中心部位移变形较大；3阶固有频率为53.9 Hz，表现为车门整体的1阶扭转振动，其中车门对角斜线位移变形较大；车门4阶固有频率为61.82 Hz，表现为弯扭组合振动，其中车门外板中心部位以及门框上部位移变形较大；车门5阶固有频率为70.11 Hz，表现为车门外板中心部位的局部振动。

3 车门实验模态分析

3.1 测试系统的组成

由于车门结构测点之间的刚度相差较大，多点激振的激励能量不能将一定频带内的激励完整表达出来。故此次试验模态采用固定单点锤击，逐点拾取响应信号。采用充气内胎支撑模拟自由-自由边界[7]，测点布置采用100 mm×100 mm间距，共有109个测点。测试系统组成如图3。

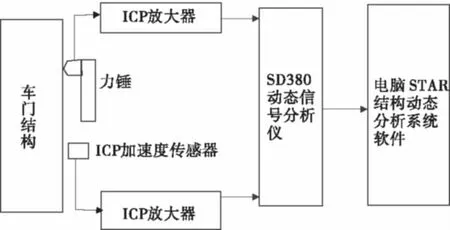
图3 车门模态试验测试系统示意Fig.3 Diagram of the modal experiment test system

激励信号与响应信号经过ICP放大器输入到SD380动态信号分析仪，经过FFT分析得到激励点与响应点之间的频率响应传递函数。在STAR分析软件中利用多项式拟合法对所有频响函数进行曲线拟合，通过模态参数识别，得到车门模态参数。

3.2 模态参数识别

模态参数的识别方法有多种，如：分量分析法、导纳圆辨识法，单参考点最小二乘法等[8]。STAR分析软件采用单参考点最小二乘法模态参数识别方法。通过响应与极点和留数之间的关系，建立自回归模型(AR模型)，通过参数估计，求出自回归系数。构造一个关于极点的Prony多项式，求出极点与留数，最终完成模态参数识别。

STAR分析软件计算车门前4阶固有频率，拟合相应振型。结果如表2，振型如图4。

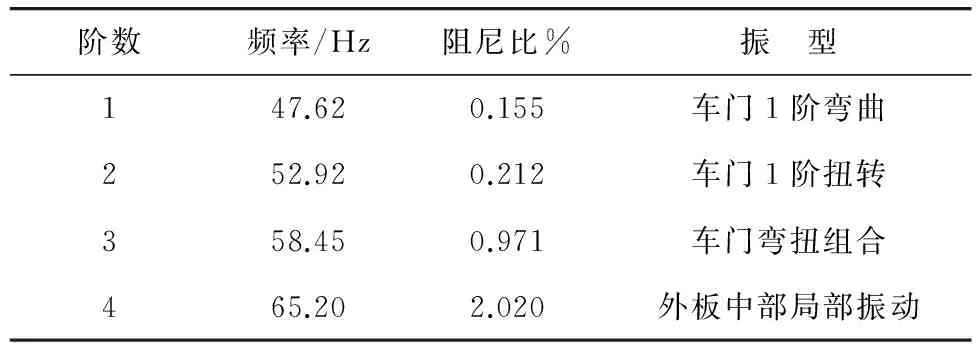
表2 车门试验模态结果 Table 2 Test modal results of car door

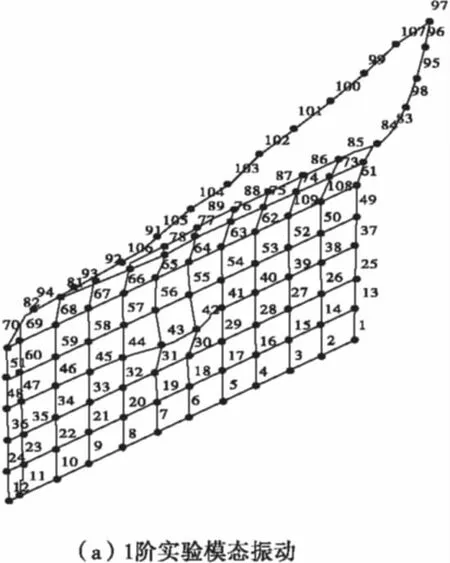
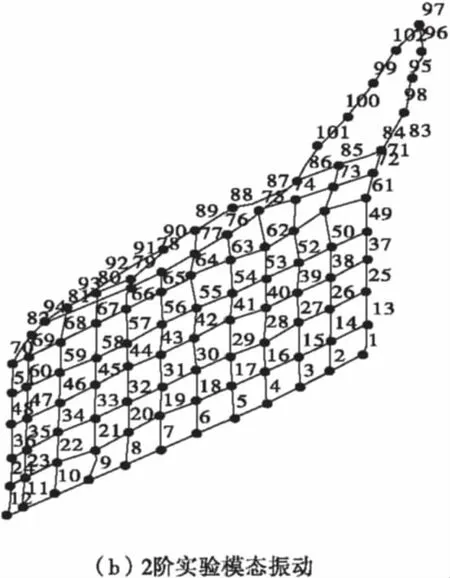
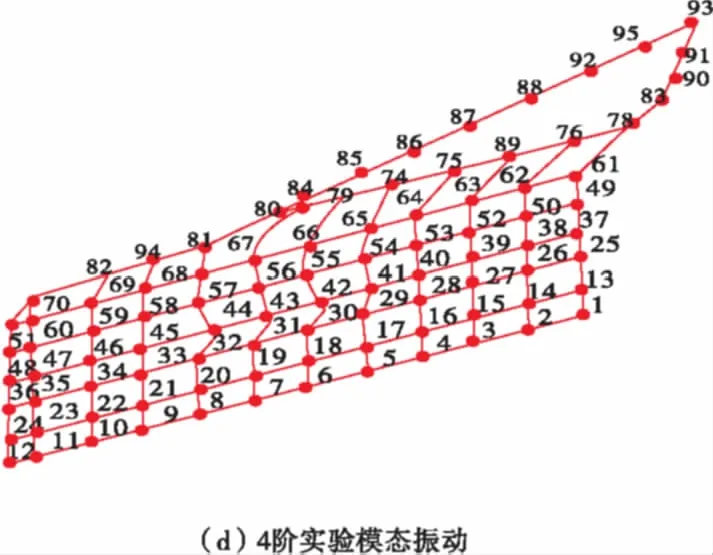
图4 1～4阶实验模态振型Fig.4 1～4 order vibration mode of test

车门1阶固有频率为47.62 Hz，振型表现为整体1阶弯曲，车门中心部位位移变化较大；车门2阶固有频率为52.92 Hz，振型表现为整体的1阶扭转振动，其中车门对角斜线位移变形较大；车门3阶固有频率为58.45 Hz，振型表现为车门整体的弯扭组合振动，车门对角斜线位移变形较大；车门4阶固有频率为65.2 Hz，振型表现为中心部位的局部振动，车门中心部位以及门框上部位移变形较大。

3.3 两种模态分析结果对比

为验证车门有限元模型，将理论模态分析结果与试验模态结果进行比较，对比结果如表3。

表3 车门计算模态与试验模态结果对比

Table 3 Comparison of FEA and mode test results of car door

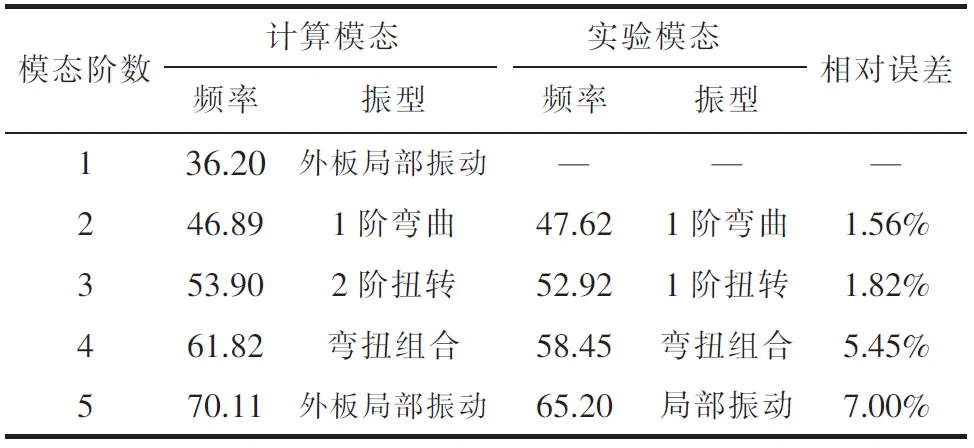
通过比较对比结果，第5阶模态频率相对误差最大，相对误差值为7%，但是能够满足小于10%的误差要求。因此，计算模态与实验模态频率相近。

由于车门有限元模型的节点数远多于模态试验中的测点数目，所以计算模态比实验模态多1阶振型。因此，理论计算模态与实验模态振型相似。

综上所述，理论计算模态与实验模态分析结果频率相近、振型相似。建立的车门有限元模型能够进一步模态灵敏度分析以及模态优化。

4 车门模态灵敏度分析及优化

4.1 车门各部件灵敏度分析

比较车门前5阶固有频率与白车身固有频率，车门1阶频率36.2 Hz与车身1阶扭转频率36.02 Hz相近、车门3阶频率53.9Hz与白车身弯扭组合频率54.1 Hz相近，存在共振可能，需进行车门模态优化。

在模态优化之前，可以通过灵敏度分析得到响应对设计变量的灵敏度值。根据灵敏度值的正负关系以及数值大小，判断影响响应的关键零部件。根据推导公式(4)，将车门9个主要组成部件板厚设定为设计变量，车门的1阶频率、3阶频率以及车门质量设定为结构响应，提交OptiStruct软件求解器，分别计算各响应对设计变量的灵敏度数值。灵敏度分析结果如表4。

如表4，不同部件的1阶频率灵敏度相差较大，其中外板、内板、外板加强板、内板加强板灵敏度值较大。1阶模态振型是外板上部的局部振动，因此外板厚度对1阶模态频率影响最大。不同部件的3阶频率灵敏度相差较大，其中内板，内板加强板，外板加强板，门锁支承板灵敏度值较大。由于车门3阶模态振型中，内板中心变形较大，因而内板厚度对3阶模态频率影响最大。不同部件的质量灵敏度值中，内板、外板、内板加强板，外板加强板灵敏度较大。由于车门内板、外板、内板加强板，外板加强板是车门主要质量承载件，其中内板厚度对质量灵敏度影响最大。

综上所述，车门外板、内板、外板加强板以及内板加强板厚度是模态优化的关键部件

4.2 车门优化分析结果

本次模态优化中，以车门外板、内板、外板加强板、内板加强板的板厚作为设计变量。以车门总质量增重不超过5%，以及车门1阶扭转频率作为约束方程。以车门1阶频率最大化作为优化目标。

优化前后关键部件厚度值如表5；优化前后车门固有频率对比以及优化后车门固有频率与白车身比较如表6，优化后，车门1阶、3阶优化模态振型如图6。

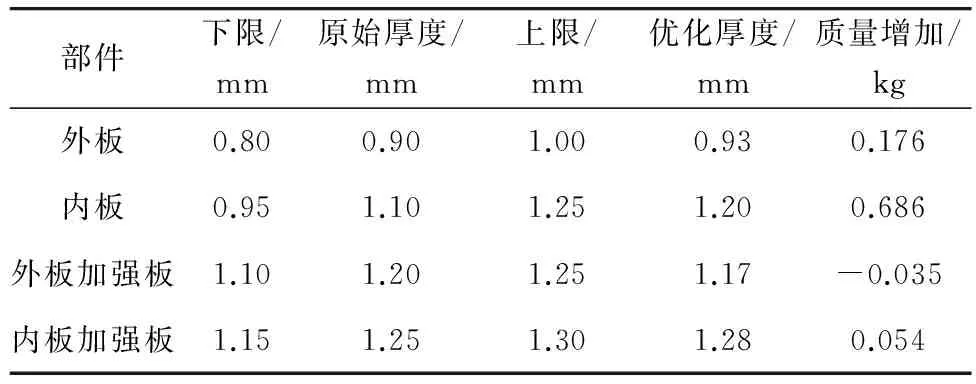
表5 车门部件灵敏度分析值 Table 5 Thickness of key components elements before and after optimization

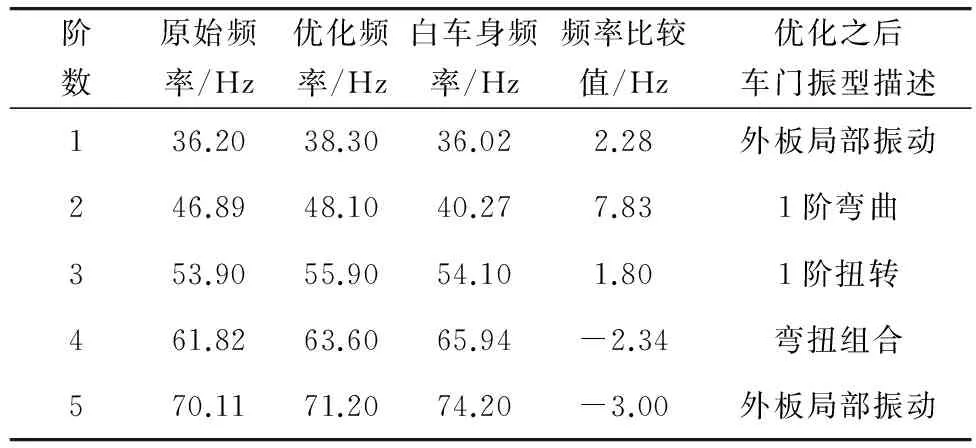
表6 优化前后车门各阶频率 Table 6 Car door frequency of each order before and after optimization

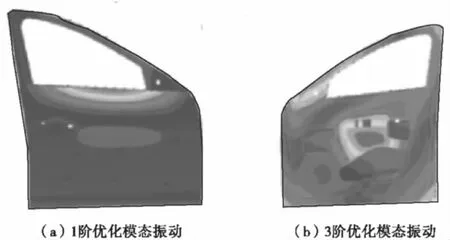
图6 1、3阶优化模态振型Fig.6 The first and third order vibration mode after optimization

优化后，车门1阶频率增加至38.3 Hz，高于白车身的1阶扭转频率2.27 Hz。车门3阶模态频率增加至55.9 Hz，高于白车身弯扭组合1.8 Hz。经过尺寸优化后，车门1阶频率、3阶频率能够有效地避开白车身固有频率，减少共振的可能。优化后车门质量增加0.881 kg，也只是占原车门质量19.37 kg的4.5%，能够满足优化约束条件。

5 结 论

1)笔者利用模态计算和模态实验相结合的方法，通过比较，得出两种方法获得固有频率相近、振型相似，从而判断有限元模型的正确性。

2)基于灵敏度分析能够准确的找到影响车门模态的关键部件。笔者通过灵敏度分析分别获得各部件板厚影响车门1阶、3阶固有频率、以及质量的灵敏度值。确定影响最大的4个部件分别是：车门外板、内板、外板加强板、内板加强板。

3)车门模态优化，质量增加0.88 kg，占原车门质量4.5%；1阶频率由原来36.2 Hz增加至38.3 Hz；3阶频率由原来53.9 Hz增加至55.9 Hz；各阶固有频率能够有效的避开白车身固有频率，提高车门模态性能。

[1] 姜连勃,王绍春.汽车车门设计(一)[J].汽车技术,1999(4):14-19.Jiang Lianbo,Wang Shaochun.Automobile body door design:I[J].Automobile Technology,1999(4):14-19.

[2] 王宏雁,徐少英.车门的轻量化设计[J].汽车工程,2004,26(3):349-353.Wang Hongyan,Xu Shaoying.A study on light-weight design of car door [J].Automotive Engineering,2004,26(3):349-353.

[3] 曹文钢，曲令晋，白迎春.基于灵敏度分析的客车车身质量优化研究[J].汽车工程,2009,31(3):278-281.Cao Wengang,Qu Lingjin,Bai Yingchun.A study on the mass optimization of bus body based on sensitivity analysis [J].Automotive Engineering,2009,31(3):278-281.

[4] 石琴，汪成明，刘钊.基于灵敏度分析的车身结构优化设计[J].合肥工业大学学报：自然科学版,2002,32(7):955-958.Shi Qin,Wang Chengming,Liu Zhao.Optimization design of structure of body-in-white based on the sensitivity analysis [J].Journal of Hefei University of Technology:Natural Science,2002,32(7):955-958.

[5] 肖成林，周德义，王志明,等.轿车车门的模态计算和组合式优化分析[J].重庆交通大学学报：自然科学版,2011,30(3):465-468.Xiao Chenglin,Zhou Deyi,Wang Zhiming,et al.Mode calculation and combined optimization of car door [J].Journal of Chongqing Jiaotong University: Natural Science,2011,30(3):465-468.

[6] 雷明准,张丰利,王建楠,等.基于有限元的车门模态分析与优化研究[J].汽车技术,2008(12):4-7.Lei Mingzhun,Zhang Fengli,Wang Jiannan,et al.Modal analysis and study on optimization of car door based on finite element method [J].Automobile Technology,2008(12):4-7.

[7] 高书娜,邓兆祥,胡玉梅.车身点焊连接有限元模拟方法研究[J].汽车工程,2008, 30(9):811-815.Gao Shuna,Deng Hoaxing,Hu Yumei.A study on the finite element modeling for spot-welds of vehicle body [J].Automotive Engineering,2006,30(9):811-815.

[8] 傅志方,华宏星.模态分析理论与应用[M].上海:上海交通大学出版社,2000.Fu Zhifang,Hua Hongxing.Modal Analysis Theory and Applications [M].Shanghai:Shanghai Jiaotong University Press,2000.