不同模型维数下常规三轴试验的离散元研究

周 杰

(重庆交通大学 土木建筑学院，重庆 400074)

0 引 言

常规三轴试验是实验室研究土体力学性质重要方法，但是实验室试验仅能获得土体的宏观力学性质，并不能获得土体的微观结构参数，故不能从本质上解释其宏观力学响应。离散元因能同时获得数值试样的宏、微观参数，而在岩土力学性质的研究中显示出很强的生命力[1-5]。罗勇，等[1]采用三维离散元数值模型对常规三轴试验进行离散元数值研究，认为三维离散元数值试验结果与实验室试验结果有良好的吻合性。虽然实验室试验试样处于三维状态，但二维离散元数值试验的计算效率快、试样微观结构的定量表达简单，因而得到了广泛的应用。周健、史旦达、蒋明镜和Li，等[2-5]借助二维离散元进行三轴试验或直剪试验的数值研究，通过分析二维数值试样的宏观力学行为，结合接触法向、颗粒旋转等微观参数的演化规律，深入研究土体宏观力学性质的微观本质。

但是，将实际的三维问题简化为二维离散元数值模型，会涉及到以下问题：离散元模型维数的减少对模拟结果有多大的影响？通过对比二维离散元数值试验结果与实验室试验结果而确定的模型参数，能否代表实验室试样本身的性质？

笔者采用离散元程序——颗粒流PFC——分别进行了实验室常规三轴试验的三维和二维离散元模拟，保证两种维数模型的材料参数和试样密实度均相同，从试样宏观力学响应和微观结构特征的角度分析模型维数对数值结果的影响。

1 数值模型与参数

实验室常规三轴试验的三维和二维离散元数值分析，即三轴和双轴离散元数值分析[6]。三轴数值试验可按照试样的实际尺寸建立圆柱形的数值试样，而双轴试验的试样为平面矩形，其宽和高分别为实验室三维试样的直径和高。为了分析试样维数对数值试验结果的影响，需保证两种维数试样的尺寸、模型参数、试样的孔隙比均相等。

1.1 三维、二维离散元数值模型的建立

为了保证本研究三维和二维数值试样的孔隙比具有可比性，制备最密实的等粒径数值试样，即三维试样颗粒在空间呈正三角锥形〔图1(a)〕排列、二维试样颗粒在平面呈正三角形〔图1(b)〕排列。

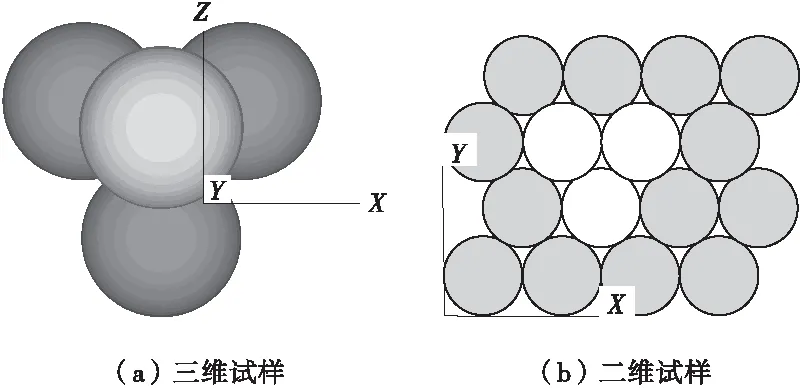
图1 数值试样内颗粒的排列结构Fig.1 Particle packing structure in 2D/3D DEM model

1.2 数值模型参数的确定

研究所进行的离散元数值试验，采用文献[6]中推荐的模型参数，如表1。对数值试样加载的水平“墙体”刚度kn=ks=1×108N/m，对试样施加围压的竖直“墙体”刚度kn=ks=1×107N/m；颗粒的摩擦系数μb=0.5，墙体的摩擦系数μw=0.0。为了消除数值试样中应力、应变的离散计算方法而产生的误差，保证数值试样内颗粒的数目大于2 000个[7]。研究中设置数值试样直径方向35个颗粒、高度方向82个颗粒，颗粒半径由程序根据试样尺寸计算确定[8]。

表1 二维和三维离散元模型参数设置

2 离散元数值试验结果分析

采用伺服控制程序对三维和二维数值试样进行剪切[9]，实现对实验室试验过程的模拟。

2.1 数值试样的宏观力学性质

三维试样和二维试样的剪切强度-剪切应变的关系曲线如图2，由于三维和二维数值试样均处于最密实的状态，故试样在剪切过程中发生明显的软化特征；围压越高，试样抗剪强度越大、其所对应的应变也越大。数值试验结果与实验室试验结果的规律一致。

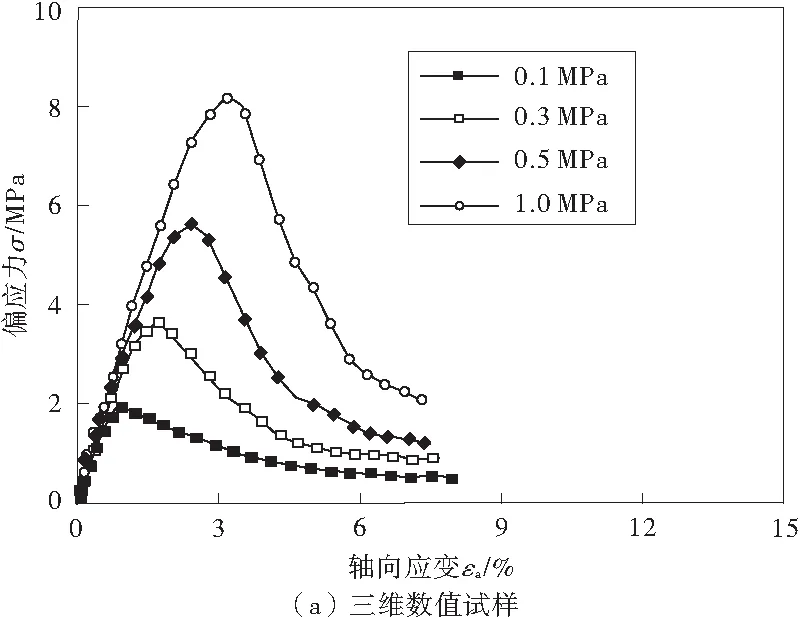
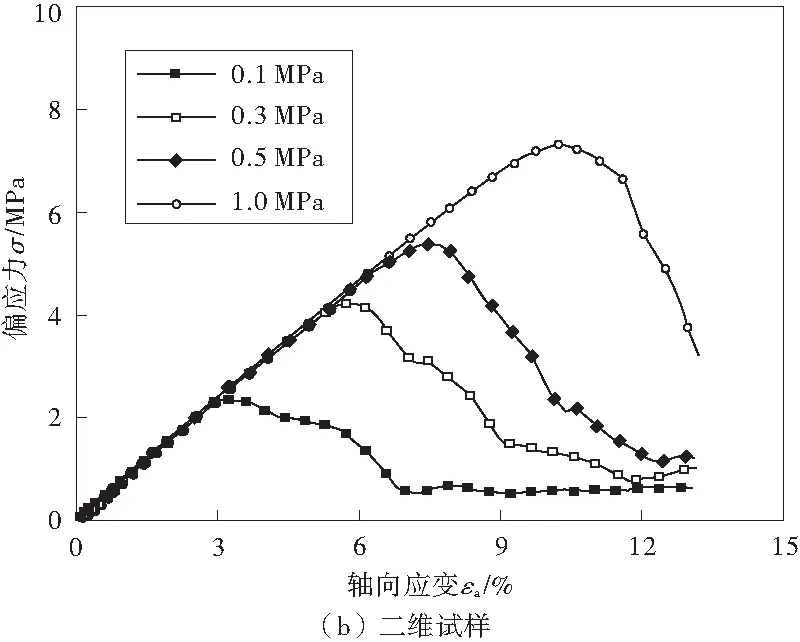
图2 数值试样的剪切应力-应变关系曲线Fig.2 Shear stress-strain curves of numerical specimens

在相同围压的作用下，三维试样达到强度峰值时的应变明显小于二维试样的峰值应变，两者之比约为1/4。当围压较低(<0.5 MPa)时，二维试样峰值强度大于三维试样的峰值强度；随着围压的增大，三维试样的峰值强度逐渐大于二维试样的峰值强度。对于文中所研究最密实的数值试样，不同维数数值试样的峰值强度在数值上相差不大，其间的差距会随试样的松散而变得明显。三维和二维数值试样的黏聚力分别为0.28和0.46 MPa、内摩擦角分别为48.7°和43.9°，由于数值试样处于理想的最密实状态，故数值试验所得试样抗剪强度指标偏大。试样黏聚力在微观上与颗粒位置调整的能力有关，而其内摩擦角在微观上与颗粒间的摩擦作用点的数目有关。三维数值试样内颗粒在空间位置调整的可能性更大，故宏观上表现为三维试样的内黏聚力较小；而三维试样内颗粒间的摩擦作用点较多，在围压作用下颗粒间的摩擦力使宏观上表现为其内摩擦角较大。三维和二维数值试样在不同围压条件下宏观力学响应的差异，本质上都是由于试样内部结构的不同、结构对外力的抵抗能力所决定的：试样内颗粒之间的约束越多、位置调整越难，则其宏观的抗剪强度越大。

由以上的分析可知，不同维数数值试样宏观力学行为的差异，本质上反映了其微观结构特征的不同。

2.2 数值试样的微观结构演化

图3为剪切破坏后(围压0.1 MPa)三维和二维数值试样的接触力链和位移场，由图3可知，三维数值试样的剪切带呈“X型”，剪切带内颗粒之间的接触力和位移均较小；试样上、下边界上或左、右边界上的接触力和位移基本相同，以“X型”剪切带为分界线，试样上、下边界附近的颗粒发生指向试样内侧的位移，而左、右边界的颗粒发生指向试样外侧的位移。二维试样的剪切带呈“XX型”，试样核心部位颗粒的位移较小；同一边界不同部位颗粒的接触力和位移明显不同，仅试样上、下边界中心部位的颗粒发生指向试样内侧的位移，其他部位的颗粒均发生指向试样外侧的位移。

为了便于定量比较三维和二维数值试样内接触法向ni的分布，笔者仅统计三维试样在x-z平面内的接触信息。定义Δθ角度范围内的接触法向密度EC(ni)为：

(1)

式中：ΔN为接触法向ni落在Δθ范围内的数目；N为试样内接触的总数目。

将研究平面内数值试样颗粒接触法向的分布表示在图4中，由于最密实三维和二维试样内颗粒均呈正三角形排列，故剪切后试样的接触法向主方向为0°，60°，120°；三维数值试样内颗粒的排列在受剪切作用的影响，剪切后少量颗粒接触法向调整为50°，90°，130°方向，三维数值试样内接触法向的分布较二维数值试样内接触法向的分布均匀。

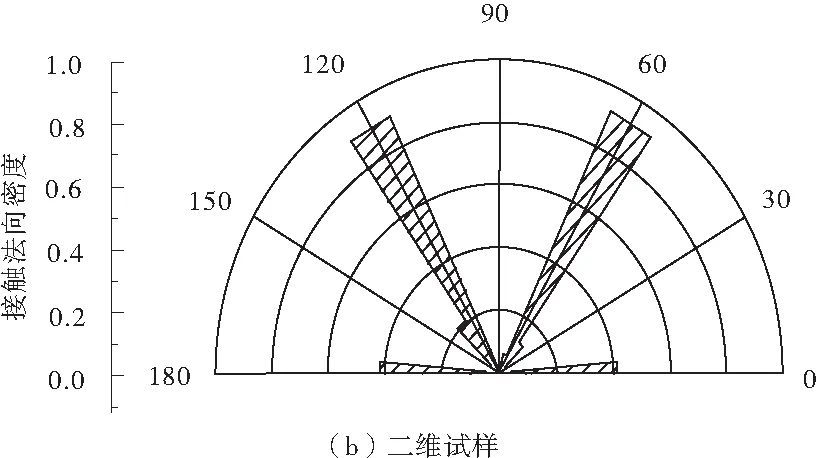
图4 破坏后数值试样的接触法向密度分布规律(围压0.1 MPa)

剪切后三维和二维数值试样的切向接触力分布规律如图5，由于三维数值试样采用球形颗粒，而二维数值试样采用单位厚度的圆盘颗粒，数值试样的接触面积不同，要使试样达到相同的围压水平，二维数值试样需要更大的外力。因此笔者关于试样内接触力的分析，仅关注两种维数数值试样接触力的分布规律。

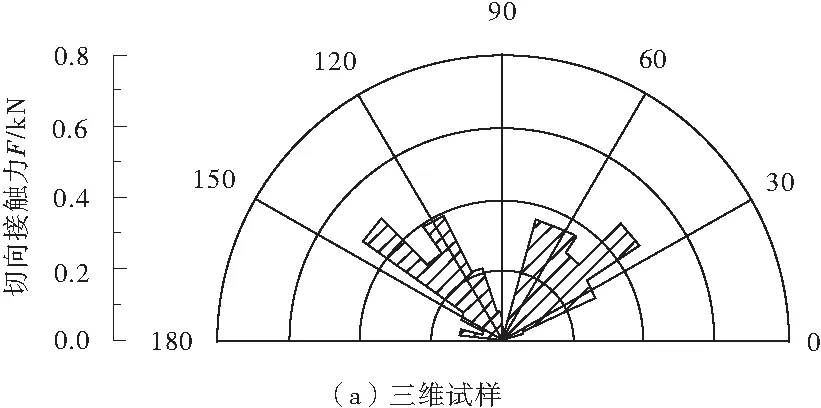
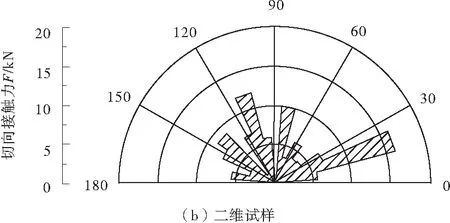
图5 破坏后数值试样的切向接触力分布规律(围压0.1 MPa)

三维试样内颗粒间的切向接触力集中在25～75°和115～145°之间，这与三维数值试样宏观上所表现出来的“X型”剪切带相一致。二维数值试样切向接触力主要集中在4个角度区间：15～25°、75～85°、105～115°和135～155°，故宏观上二维试样的剪切带为“XX 型”。试样内切向接触力的微观分布规律与宏观剪切带的一致性，进一步证明了试样微观结构对宏观响应的决定性作用。

当试验围压由0.1 MPa增大至1 MPa时，三维试样的剪切带由“X型”变为“◇型”，二维试样的剪切带也由“XX型”变为“X型”。围压增大，试样剪切带的范围趋于集中(图6)。

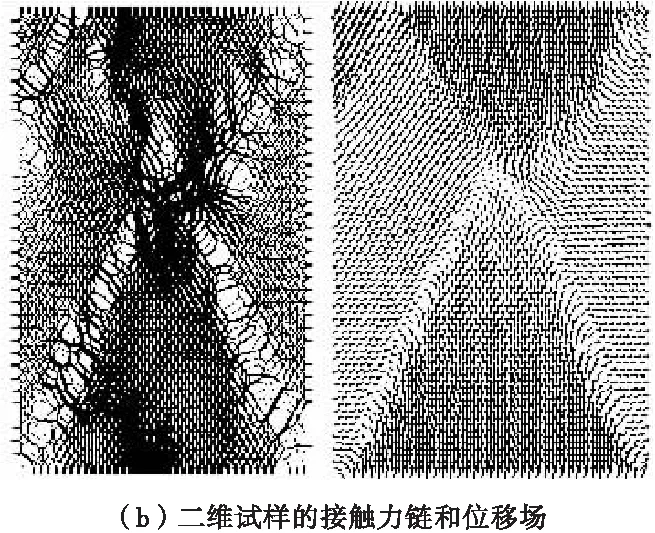
图6 破坏后数值试样的接触力链和位移场(围压1 MPa)

分析图7所示试样内切向接触力的分布规律可知，围压增大至1 MPa后，三维试样内颗粒间的切向接触力集中在45～65°和115～145°范围内，二维数值试样内颗粒间的切向接触力集中在35～75°、105～125°和155～165°范围内。围压增大使二维和三维试样的切向接触力的分布更加集中，其方向接近接触法向的分布方向(0°，60°，120°)上，与宏观上试样剪切带的变化规律一致。

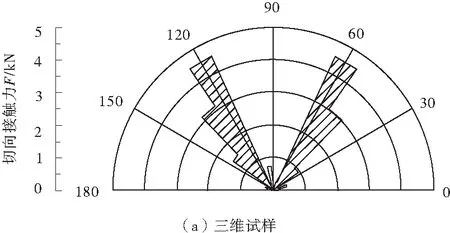
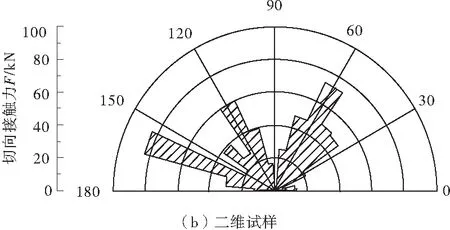
图7 破坏后数值试样的切向接触力分布规律(围压1 MPa)

3 结 论

针对实验室常规三轴试验，进行了最密实状态的、参数相同的三维和二维的离散元数值分析，通过分析数值试样的宏观力学响应和微观结构特征，获得了以下结论：

1)最密实三维和二维数值试样在剪切过程中均表现出软化的力学性质，随围压的增大，不同维数试样峰值强度增大，三维试样的峰值强度逐渐大于二维试样的峰值强度；不同围压下，三维试样峰值强度所对应的应变一直约为二维试样的1/4倍。

2)由于数值试样处于理想的最密实状态，故数值试验所得试样抗剪强度指标偏大：三维和二维数值试样的黏聚力分别为0.28和0.46 MPa、内摩擦角分别为48.7°和43.9°。试样黏聚力在微观上与颗粒位置调整的能力有关，内摩擦角在微观上与颗粒间的摩擦点的作用有关。

3)在相同围压下，三维和二维试样宏观剪切带的形状不同，试样切向接触力的集中方向决定了其宏观剪切带的形状。围压的提高使二维和三维试样内切向接触力的分布均变得更加集中在接触法向主方向范围内，宏观上表现为试样剪切带变得集中。

三维和二维数值试验结果的差异表明，在利用简化的二维离散元模型分析实际的三维问题时，不能一味追求数值试验与物理试验在数量上的一致，而应发挥二维试样在微观结构定量分析方面的优势，从机理上解释试样的宏观力学性质，努力建立能描述试样宏观力学响应与其微观结构演化之间的定量规律。

[1] 罗勇,龚晓南,连峰.三维离散颗粒单元模拟无黏性土的工程力学性质[J].岩土工程学报,2008,30(2):292-297.

Luo Yong,Gong Xiaonan,Lian Feng.Simulation of mechanical behaviors of granular materials by three-dimensional discrete element method based on particle flow code [J].Chinese Journal of Geotechnical Engineering,2008,30(2):292-297.

[2] 周健,池永.砂土力学性质的细观模拟[J].岩土力学,2003,24(6):901-906.

Zhou Jian,Chi Yong.Mesomechanical simulation of sand mechanical properties [J].Rock and Soil Mechanics,2003,24(6):901-906.

[3] 史旦达,周健,刘文白,等.砂土直剪力学性状的非圆颗粒模拟与宏细观机理研究[J].岩土工程学报,2010,32(10):1557-1565.

Shi Danda,Zhou Jian,Liu Wenbai,et al.Exploring macro-and micro-scale responses of sand in direct shear tests by numerical simulations using non-circular particles [J].Chinese Journal of Geotechnical Engineering,2010,32(10):1557-1565.

[4] 蒋明镜,王富周,朱合华.单粒组密砂剪切带的直剪试验离散元数值分析[J].岩土力学,2010,31(1):253-258.

Jiang Mingjing,Wang Fuzhou,Zhu Hehua.Shear band formation in ideal dense sand in direct shear test by discrete element analysis [J].Rock and Soil Mechanics,2010,31(1):253-258.

[5] Li Xia,Yu Haisui.Influence of loading direction on the behavior of anisotropic granular materials [J].International Journal of Engineering Science,2009,47(11/12):1284-1296.

[6] Itasca Consulting Group,Inc.PFC2D (Particle Flow Code in 2 Dimensions),Version 3.10 [M].Minneapoli:ICG,2002.

[7] 史旦达.单调与循环加荷条件下砂土力学性质细观模拟[D].上海:同济大学,2007.

Shi Danda.Micromechanical Simulations of Sand Behavior under Monotonic and Cyclic Loading [D].Shanghai:Tongji University,2007.

[8] 周国庆,周杰,陆勇,等.颗粒流程序(PFC-2D)中阻尼参数的适用性研究[J].中国矿业大学学报,2011,40(5):662-667.

Zhou Guoqing,Zhou Jie,Lu Yong,et al.Selection of damping parameters used in particle flow code (PFC-2D) [J].Journal of China University of Mining & Technology,2011,40(5):662-667.

[9] 周杰.砂土制样过程的仿真试验及宏-微观分析[D].徐州:中国矿业大学,2011.

Zhou Jie.Multi-Scale Investigation on the Effect of the Specimen Preparation on Sand Behavior [D].Xuzhou:China University of Mining & Technology,2011.