基于高斯混合模型的类人机器人果实辨识研究

陈 宇，黄仲洋，江露，钟秋波

(东北林业大学信息与计算机工程学院，黑龙江哈尔滨150040;2.宁波工程学院，浙江宁波315000)

进入21世纪，机器人研究取得了重大进展。全自主仿人机器人是仿人机器人研究中非常热门的一个领域，许多大学或研究机构都对其投入了巨大的精力。嵌入式视觉系统是全自主仿人机器人系统的基础，它对机器人的总体性能起着决定性作用，机器人对目标的识别是建立在视觉系统基础上的［1-2］。

果实颜色是果实非常直观的重要特征，不同果实的颜色差别很大，这样就能有效提取果实特征，从而对果实进行识别。过去工作主要依靠人工完成，耗时耗力并且效率低下，借助计算机提高了工作效率，并将此技术和类人机器人结合，大大提高了分析的准确性。

类人机器人自带的摄像头作为视觉，通过摄像头获取彩色图像。传统的彩色图像分析是基于RGB色度空间的，但是RGB空间是颜色显示空间，并不适合人的视觉特性，而HSV色度空间能很好地体现出人眼辨别颜色的特点，在HSV空间，图像特征明显，易于处理［3］。因此该研究采用HSV色度空间对图像进行颜色提取。

将颜色作为果实特征后，结合高斯混合模型算法，对颜色进行辨识，从而达到对果实的辨识。高斯混合模型算法满足收敛条件并且提高了识别的效率，试验结果表明，该算法是有效的，与BP神经网络、SVM支持向量机、决策树的识别算法相比，基于高斯混合模型的果实识别算法获得了较高的识别率，取得了很好的试验效果。

1 果实颜色提取

1.1 颜色空间的选择 要处理彩色图像，首先要选取合适的颜色空间。颜色空间指的是某个三维颜色空间中的一个可见光子集。它包含某个颜色域的所有颜色。颜色空间的用途是在某个颜色域内方便地指定颜色。一般，图像常采用RGB三元色彩色空间表示，但RGB三色空间中两点间的欧氏距离与颜色距离不呈线性比例，换句话说，就是颜色受亮度的影响很大，RGB颜色空间不具有进行彩色图像处理所要求的独立性和均匀性指标。所谓独立性是指颜色空间的3个分量互不影响，对于其中某个分量的处理不导致其他分量相对于人眼感觉发生变化。而均匀性是指对颜色空间中的每一个分量来说，相同的处理改变量在不同的取值处应引起相同的视觉变化。然而绝对满足独立性和均匀性的颜色空间是不存在的［4］，只能根据实际情况，找到一种能在较大范围内符合上述两个条件的颜色空间。为更好地进行颜色辨识，通过试验，该研究采用了HSV颜色空间。

1.2 HSV色度空间变换原理 摄像头获取的图像一般为RGB图像，因此先要将颜色空间从RGB转换到HSV。如图1，HSV 色彩空间是一个六棱锥体，0≤H≤360，0≤S≤1，0≤V≤1，对于 R、G、B∈［0，1］，RGB 空间到 HSV 空间的映射过程如下:

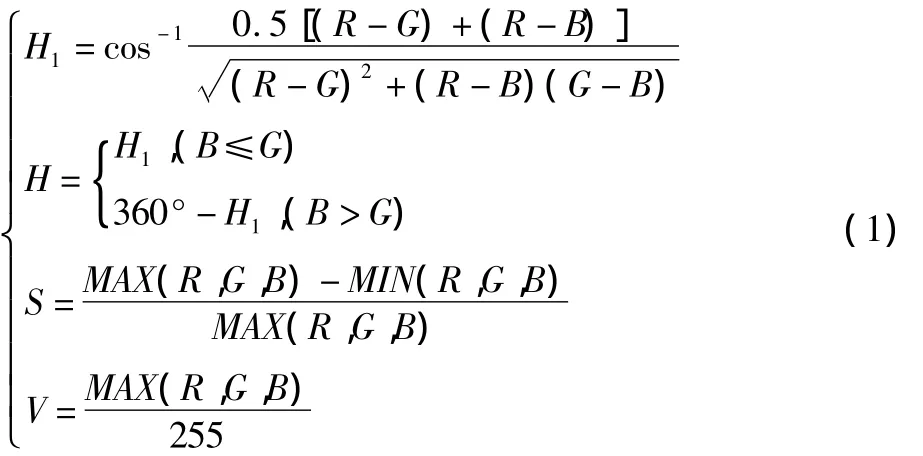
2 高斯混合模型算法原理

果实识别算法有BP、贝叶斯、决策树等，但高斯混合模型试验得到了较好的效果，识别率较高。

图1 HSV色彩空间

高斯混合模型是一种常用的描述混合密度函数分布的模型，矢量特征在概率空间的分布状况通过若干个高斯概率密度函数的加权和进行描述。即每个高斯混合模型是由K个Gaussian分布构成，1个 Guassian是“Gomponent”，形成多个分类器，对Gomponent进行线性加和形成混合高斯模型的概率密度函数［5］:

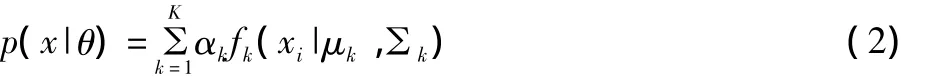
式中，xi是 d 维矢量;θ=(μ1，μK，Σ1，Σk)，为高斯混合分布参数;αk是加权的系数，代表选中每个Component的概率，需要满足限制条件是 Component的高斯概率密度分布，如下:

式中，μk是均值;Σk是协方差矩阵。

GMM模型的各个分量是通过均值和方差表示的，GMM的分类过程是以均值为中心的椭圆体分布，方差决定它的几何性质。使用高斯混合模型对流型样本分类，首先对未知参数 K、αk、μk、Σk的值进行初始化，才能构造 GMM 模型，对概率密度函数建模。果实样本分为5类:香蕉、西瓜、番茄、葡萄、苹果。因此参数K=5，对于剩余3个参数的估计有多种方法，使用的比较频繁的是EM算法。

EM算法也称作期望最大算法，是对参数的最大似然估计，此算法主要应用在如下方面:①对不完整数据的估计;②假设缺失的数据存在，降低似然函数复杂度［6］。

EM算法的执行过程［7］如下。

首先，计算期望(Expectation)，估计隐含变量。观测数据确定，对完整似然函数的期望计算。

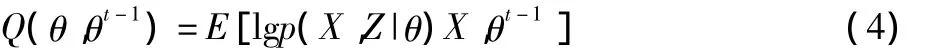
式中，θk-1是当前的参数估计值;θ是更新后的参数值。

然后，计算极大值，估计其他参数。求解θ，使 Q(θ，θk-1)得到极大值，即:

在高斯混合模型中，样本数据由不完整数据构成，则加入隐含变量 Z={z1，z2，…，zN}，zi=(zi1，zi2，…，zik)独立分布于K类，隐含变量的概率分别为α1，…，αk，满足如下:

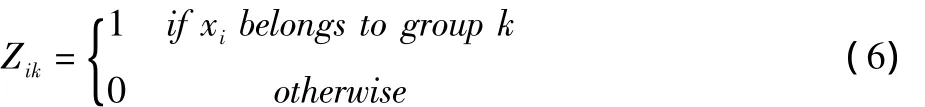
算法执行过程中对数似然函数定义为:

式中，p(k|xi，θt-1)是K类分布的后验概率:

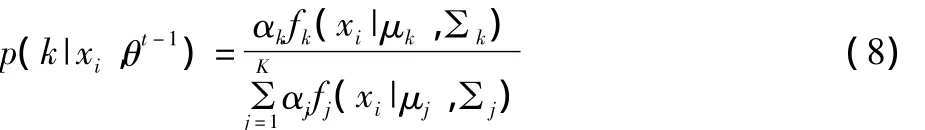
使用梯度法求解条件极值，可得如下关系式:

即:

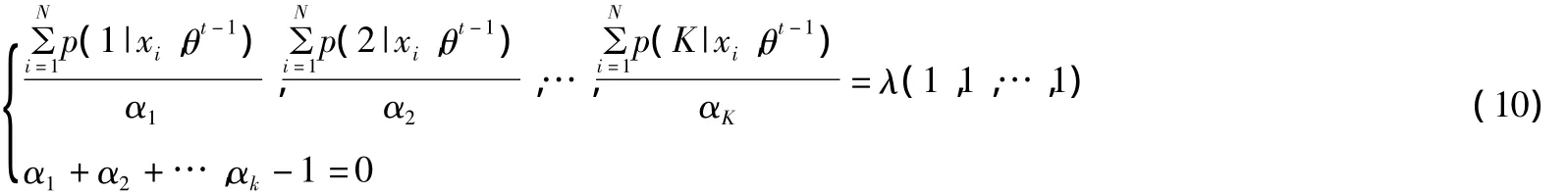
其中:

对 Q(θ，θt-1)，求其关于 μk、Σk的导数，让其为 0，可得均值重估公式:

方差重估公式:

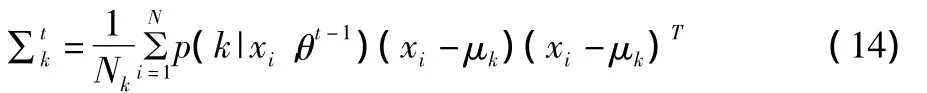
迭代终止的条件就是迭代重估公式，直到满足预先设定的条件。EM算法涉及的理论比较简单和单一，其主要优点是简单和稳定，每次迭代都能保证观察数据对数似然是增大的。但EM算法也有其缺点，主要是收敛速度慢，尤其当输入的数据维数过高或者规模过大时，将严重影响收敛速度。EM算法能找到局部最大点，但对于找全局最大点比较困难［8］。EM算法的初始化有严格的要求，对于不同的初始值，能够使得结果有较大差异［9］。目前最有效的方法是将Kmeans算法与EM算法相结合，使用Kmeans算法来计算群聚中心点，当作EM参数中均值的初始输入值。

Kmeans聚类是聚类算法中常用的算法［10］。该算法输入参数K，将输入特征矩阵划分为K个聚类，相同聚类对象的相似度较高，反之较小。主要思想是:选取K个中心点聚类，对最靠近中心点的对象归类，通过迭代的方法，逐次更新各聚类中心的值，直至得到最好的聚类结果［11］。得到各个聚类的中心点之后，将其作为EM算法初始值。该算法使用的很广泛，尤其是和EM算法相结合，先对初始数据进行粗略分类，再将得到的数据作为参数估计初始化的数据。将这两种算法结合能提高EM算法收敛的速度和分类的正确率。

3 仿真与试验

由于季节等试验条件的原因，该试验均为类人机器人对不同果实图片的识别，见图2。

图2 类人机器人果实辨识试验

图3显示了类人机器人识别的果实图像样本及HSV颜色直方图。

该试验每类果实收集样本30个，共150个，其中随机选取每类中20个作为训练样本，其余样本作为测试样本。该试验总共测试数据为50组，果实识别效果如表1所示。

表1 试验结果

4 结论

该试验设计了一个具有视觉的能够识别果实的类人机器人系统，通过采集图像，获取目标信息，采用HSV颜色空间，结合高斯混合模型算法，通过训练得到每类果实所对应的分类器模型参数，构造分类器，实现了类人机器人对果实准确高效的识别。

图3 果实样本图片及HSV颜色直方图

［1］张勇.足球机器人识别算法和决策仿真［D］.长沙:湖南大学，2002.

［2］陈凤东，洪炳，朱莹.基于HIS颜色空间的多机器人识别研究［J］.哈尔滨工业大学学报，2004，36(7):928-930.

［3］张全海，施鹏飞.基于HSV空间彩色图像的边缘提取方法［J］.计算机仿真，2000，17(6):25-27.

［4］ZHARALIC R M，SHAPRO L G.Computer and robot vision［M］.New-York:Addisiona-Wesely，1992:105-120.

［5］岳佳，王士同.高斯混合模型聚类中EM算法及初始化的研究［J］.微计算机信息，2006，11(3):244-246.

［6］王鑫.基于高斯混合模型的聚类算法及其在图像分割中的应用［D］.太原:中北大学，2013.

［7］庞强，邹涛，丛秋梅，等.基于高斯混合模型与主元分析的多模型切换方法［J］.化工学报，2013(8):2938-3946.

［8］曹红丽.混合高斯模型的混合EM算法研究及聚类应用［D］.乌鲁木齐:新疆大学，2010.

［9］焦宾，吕霞付，陈勇，等.一种改进的自适应高斯混合模型实时运动目标检测算法［J］.计算机应用研究，2013(11):3518-3520.

［10］JAMSHIDIAN M，JENNRICH R I.Conjugate gradient acceleration of the EM algorithm［J］.Journal of the American Statistical Association，1993，88:221-228.

［11］CAO J，WU Z，WU J J，et al.Towards information-theoretic K-means clustering for image indexing［J］.Signal Processing，2013，93(7):2026-2037.