多Agent MDPs中并行Rollout学习算法
李 豹
(中国人民银行芜湖市中心支行,安徽芜湖 241000)
目前,多Agent学习已成为人工智能领域的热点,大多数研究工作是基在于Markov对策(Markov games)理论框架下研究.和单Agent学习不同,多Agent学习在Agent选择动作或行为时,需要考虑所有Agent值函数的某种平衡解(equilibrium Learners),因此在本质上,Markov对策可看成是将马尔科夫决策过程(MDPs)从单Agent扩展到多Agent领域.其算法成果包括Minimax-Q学习算法和Friend-or-Foe-Q(FFQ)学习算法[1-2]、Nash Q学习算法[3]、CE-Q学习算法[4]等.在实际中,大多数多Agent系统,由于系统本身自有的特点,在多Agent学习时,其状态空间和行动集合往往特别巨大.同时,多Agent之间行为预测也会扩大空间需求,为此,需要研究逼近的方法来降低空间需求.使用神经元动态规划(NDP)理论来逐步逼近求解取得了重要的理论和应用成果[5-8].
Bertsekas等在1997年提出了一个仿真优化Rollout算法[9-10].它有两个优点:一是Rollout算法新策略即能通过离线仿真也可通过在线计算得到,并且比TD学习和Q学习优化波动小.二是rollout算法有较强的并行性,更容易在多核系统或计算机集群上并行求解.从这两点来,rollout算法更具有实际可操作性.文献[11-12]发展了MDP性能势的相关理论,为MDP性能分析和优化提供了新的理论框架,产生许多基于理论计算或仿真的优化算法[13-14],性能势既能通过泊松方程求解得到,也能通过一条样本轨道仿真学习得到,它因而能和Rollout算法很好地结合.
1 多Agent MDPs模型
定义1 Markov对策.Markov对策(MG)通常有5元组构成.其中n表示多个Agent的数量.X表示Agent的状态集合.Ai表示Agent的行动集合.P表示Agent的状态转移概率函数.fi表示Agenti的立即报酬代价函数X×A→f.
在单Agent MDPs中,时间t下,Q学习更新公式为

其中,αt为学习步长,可为常数或衰减步长,γ为折扣因子.
由于单Agent无需考虑与其他Agent通信,其本质上就是经典的马尔科夫决策过程.而多Agent需要所有Agent互相协作完成整个问题的求解,多Agent学习后Q值更新公式为

∈A定义为Agenti可选的行动集合,A为所有Agent的联合行动空间,A=A1×A2×…×An.定义为Agenti在状态中选择某种Nash平衡下的值函数,其算法有Minimax-Q、FFQ、Nash-Q及CE-Q学习等.
定义2 性能势.性能势理论为MDP的优化提供了一个统一的框架,运用性能势理论,从泊松方程入手,可以在较少的假设条件下建立起MDP基于性能势的最优性原理和最优性方程,且容易证明其最优解的存在性定理.另一方面性能势也可以定义在一条样本轨道上,在系统模型未知的问题中可以建立基于样本轨道的仿真和在线优化算法.文献[12]中给出了性能势理论,Agenti在状态x下的性能势为
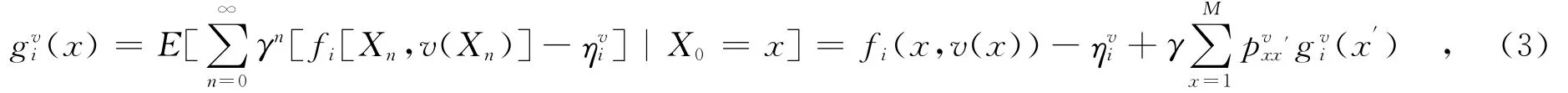

2 基于rollout思想的多Agent学习算法
在单Agent的Q学习算法中,更新Q值原则是按照最优行动集合时的折扣累计代价值,而Rollout算法是建立一个初始策略v0,通过rollout产生更新策略v1,更新策略比初始策略更能接近Nash最优平衡解.文献[6]中,在性能势理论框架下给出了rollout算法.基于此,Rollout算法Q值更新公式为
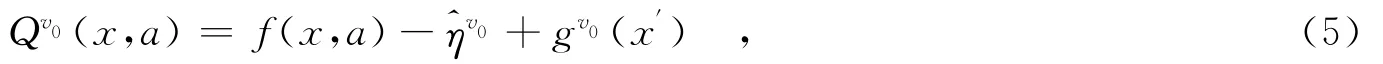
将rollout算法推广到多Agent学习中得到如下算法1.
算法1 Multi-Agent rollout algorithms for Agenti
Step1:初始策略v0,精度ε;Step2:对于Agenti,由初始策略v0仿真学习得到性能势和平均代价对于状态x∈X,随机选择一个行动a∈Ai,通过状态转移概率仿真下一个状态x′,计算求得状态x所有行动a的按下式计算

作为状态x的更新行动,这样构成新策略v1;Step4:如果达到收敛条件,算法结束;否则令v0=v1,转step2.v1(x)表示在x状态在所有Agent的Nash平衡解下对应的更新策略,Nash平衡解可利用多AgentQ学习得到,例如使用极小极大学习的计算公式为


算法1中,由v0得到的性能势gv0结果,需要建立状态与性能势的一一对应数据表格,当系统状态空间很大时,易造成“维数灾”.我们可以利用神经元动态规划方法,用一条神经网络来近似逼近性能势.此时计算机保存是神经元网络的逼近结构,而不是状态和性能势的一一对应关系,从而加快算法的执行效率.
当Agent数量过大或每个Agent的状态空间过多时,可能需要花费很长的时间才能获得满意的解,这对于那些实时性要求高的系统有很大局限.我们可以设计并行算法来加快学习收敛速度,真正地降低算法的执行时间.并行算法的设计一般从串行算法入手,寻找可并行部分,包括划分、计算、同步等阶段[15].多Agent rollout算法可并行部分有:多个Agent学习、Agent的行动集合、Agent的状态集及Nash平衡解的计算等.此外,若用神经元网络逼近性能势,神经网络划分等也可以采用并行算法.
本文采用划分行动集合的并行思想,即每个处理节点只初始化和更新某些行动集合,利用消息传递接口框架(Message Passing Interface,MPI)建立并行算法如算法2.
算法2 Multi-Agent parallel rollout algorithms for Agenti.Step1:(划分阶段)假设有H个处理节点,将候选的行动集合D(i)划分H个子集{U1,U2,…,UH}节点i只处理Uh;Step2:(计算阶段)按照算法1,计算状态-行动对进行全收集操作,将每个处理节点中收集起来;Step4:(计算阶段)按照算法1的公式(6)计算v1(x),并将v1(x)广播(MPI_Bcast)到所有处理节点;Step5:若满足终止条件,结束算法;否则转Step2.算法2的Step3中,MPI_ALLgather和MPI_Bcast为MPI中定义的标准函数,前者表示把各个处理节点中某个变量全收集到每个处理节点中,后者含义是将某个变量广播到所有处理节点中[15].
衡量算法2性能需考虑并行加速比和执行效率.并行加速比=并行执行总时间/串行计算时间,执行效率为并行加速比/处理节点数.并行加速比越高,表明并行计算获得性能提升越好;执行效率越高,表明
算法1中,由v0得到的性能势gv0结果,需要建立状态与性能势的一一对应数据表格,当系统状态空间很大时,易造成“维数灾”.我们可以利用神经元动态规划方法,用一条神经网络来近似逼近性能势.此时计算机保存是神经元网络的逼近结构,而不是状态和性能势的一一对应关系,从而加快算法的执行效率.
当Agent数量过大或每个Agent的状态空间过多时,可能需要花费很长的时间才能获得满意的解,这对于那些实时性要求高的系统有很大局限.我们可以设计并行算法来加快学习收敛速度,真正地降低算法的执行时间.并行算法的设计一般从串行算法入手,寻找可并行部分,包括划分、计算、同步等阶段[15].多Agent rollout算法可并行部分有:多个Agent学习、Agent的行动集合、Agent的状态集及Nash平衡解的计算等.此外,若用神经元网络逼近性能势,神经网络划分等也可以采用并行算法.
本文采用划分行动集合的并行思想,即每个处理节点只初始化和更新某些行动集合,利用消息传递接口框架(Message Passing Interface,MPI)建立并行算法如算法2.
算法2 Multi-Agent parallel rollout algorithms for Agenti.Step1:(划分阶段)假设有H个处理节点,将候选的行动集合D(i)划分H个子集{U1,U2,…,UH}节点i只处理Uh;Step2:(计算阶段)按照算法处理节点的使用率越高.
3 实例求解
考虑一个多级仓库商品库存控制问题,把每级仓库看出一个Agent,多级仓库商品库存控制构成了一个典型的多Agent MDPs.
实例1:假设一种商品的仓库共有两级,商品需求量符合λ=4的泊松分布,两级仓库商品的单位定购费均为10,库存费为10,缺货损失费为20,第1级仓库总容量为20,第2级仓库总容量为16.该多Agent系统的状态数量为21×17=357个.
因为这两级仓库是纯团队合作的关系,即若每级仓库利益最大化,那么两级仓库也能达到最大整体利益,团队Q值更新公式为

利用(9)更新公式求解上例,得到结果如表1.由表1可知,进行6次迭代后,实验结果依然保持不变,这表明实验结果已收敛.agenti=1时,rollout算法运行实验结果如图1所示.

图1 算法1求解例1迭代结果(Agent i=1)

表1 算法1求解例1结果
实例2:为验证Rollout算法的并行效果,考虑一个状态集合较多库存问题.假设5级仓库,每级仓库容量均为6,各级仓库商品的库存费用Cb={5,3,4,2,3},缺货损失费用Cl={6,8,7,8,9},定购费用Cd={2,3,5,3,6},需求量分布为:λ1=2,λ2=3,λ3=1,λ4=2,λ5=3泊松分布,系统状态为16 807个.
若使用Q学习算法求解该例,在计算机中保存的是Q因子(状态-行动对),由于状态集合很大,往往会出现“维数灾”,导致问题不可解.而使用rollout算法,利用性能势理论,借助于神经元动态规划的泛化能力,将性能势的计算从高维空间映射到低维空间,从而节约存贮空间,在上例中可使用28×15×1BP神经网络逼近性能势,二值化后,28×15×1网络结构最多可表示16384个状态,而28×15×1网络结构只有435个权值,这样大大减少了内存的消耗.令迭代次数为20,在MPIICH2-1.0.5环境,CPU为双至强E5620(8个处理节点)的高性能服务器下,使用并行处理算法2得到的实验结果如表2所示.由表2还可以看出,当库存控制状态数增大时,并行执行效率总体是趋优的.

表2 算法2求解例2的实验结果
4 结论
Rollout算法是一个很好的逼近最优解算法.在多Agent学习中,在性能势的框架里运用Rollout算法,使用神经元网络逼近性能势,既可以解决模型未知的情况克服“建模难”的问题,也可以大大减少多A-gent学习程序对空间的需求,从而克服“维数灾”的问题.同时,由于Rollout算法比其他仿真算法具有更强的内在并行性,在rollout算法基础上进行多Agent学习,具有良好的可行性和有效性.
由于多Agent学习重要的一点是如何计算和选择平衡解的问题.在本文中,利用已有多Agent Q学习的求平衡解算法,如何在性能势的框架内,利用rollout算法本身的特点建立更优秀算法是下一步所要考虑的问题.
[1] Littman M.Markov games as a framework for multi-Agent reinforcement learning[C]//Proceedings of the Eleventh International Conference on Machine Learning.San.Francisco:Morgan Kaufmann Publishers,1994:157-163.
[2] Littman M.Friend or foe Q-learning in general-sum Markov games[C]//Proceedings of Eighteenth International Conference on Machine Learning.Williams,College,MA,San Mateo,CA:Morgan Kaufmann Publishers,2001:322-328.
[3] Hu J,Wellman M.Nash Q-learning for general-sum stochastic games[J].Machine Learning Research,2003,4:1 039-1 069.
[4] Greenwald A,Hall K.Correlated Q-learning[C]//Proceedings of the Twentieth International Conference on Machine Learning.Washington DC,USA:AAAI Press,2003:242-249.
[5] 殷保群,奚宏生,周亚平.排队系统性能分析与Markov控制过程[M].合肥:中国科学技术大学出版社,2004.
[6] 李豹,程文娟,周雷,等.rollout及其并行求解算法在多类商品库存控制中的应用[J].系统仿真学报,2007,19(17):3 883-3 887.
[7] Bertsekas D P.Dynamic Programming and Optimal Control,Vol.Ⅱ,4th Edition:Approximate Dynamic Programming[M].Belmont:MA,Athena Scientific,2012.
[8] Sutton R S,Barto A G.Reinforcement learning:an introduction[M].Cambridge:MA,MIT Press,1998.
[9] Bertsekas D P,Tsitsiklis J N,Wu C.Rollout algorithms for combinatorial optimization[J].Heuristics,1997,3:245-262.
[10]Bertsekas D P.Rollout Algorithms for Discrete Optimization:A Survey[C]//Handbook of Combinatorial Optimization.Berlin:springer,2005:2 989-3 014.
[11]Li X,Cao X R.Performance optimization of queueing systems with perturbation realization[J].European Journal of Operations Research,2012,218(2):293-304.
[12]Cao X R.Stochastic Learning and Optimization-A Sensitivity-Based Approach[M].New York:Springer,2007.
[13]Cao X R,Wang D X,Lu T,et al.Stochastic Control via Direct Comparison[J].Discrete Event Dynamic Systems:Theory and Applications,2011,21:11-38.
[14]Yin B Q,Lu S,Guo D.Analysis of Admission Control in P2P-Based Media Delivery Network Based on POMDP[J].International Journal of Innovative Computing,Information and Control,2011,7(7B):4 411-4 422.
[15]陈国良.并行算法的设计与分析[M].北京:高等教育出版社,2009.

