多帧图像超分辨率重建算法的研究

王 静，吴爱弟

（天津职业技术师范大学理学院，天津 300222）

多帧图像超分辨率重建算法的研究

王 静，吴爱弟

（天津职业技术师范大学理学院，天津 300222）

多帧图像超分辨率重建技术就是将一些变形、模糊、降采样的多幅低分辨率图像进行融合估计出一幅高分辨率图像。其步骤主要分为：运动估计、插值处理、图像重建。本文采用Vandewalle配准方法将处理过的低分辨率图像序列映射到一幅高分辨率网格上，然后进行插值，最后结合小波变换和迭代方法进行图像重建。并采用小波阈值去噪方法进行去噪处理。实验结果表明本文算法能很好的提高图像的峰值信噪比，是图像重建的一种有效方法。

超分辨率图像重建；运动估计；插值；小波变换；阈值去噪

1 引言

在图像系统中，从图像的获取，到图像的传送、接受、输出等等一系列环节，都会受到系统的物理条件和外界因素的干扰，从而使得人们最终获取的图像的分辨率降低，针对这些因素，又为了满足人们的实际需要，图像超分辨率重建技术应运而生。超分辨率图像重建就是将一系列分辨率较低、质量较差的低分辨率图像在像素级进行序列融合，从而得到分辨率较高、质量更好的图像。自1984年，Tsai和Huang首次提出了基于序列或多帧图像的超分辨率重建算法之后，超分辨率重建技术成为人们关注的焦点，该技术得到了较快的发展，也取得丰硕的研究成果。其方法主要是分为频域方法和空域方法两大类。超分辨率图像重建方法无需改变成本较高的物理硬件设施，从软件的角度，改变图像的分辨率，既经济又实用。并广泛应用到军事领域、航天领域，医疗卫生安全领域等等[1-3]。

多帧图像的超分辨率图像重建，即将一些变形、模糊、降采样、噪声混叠后的多幅低频图像进行融合估计出一幅高分辨率图像或图像序列。

近些年，随着小波理论的成熟，人们越来越多地将其引入到图像超分辨率重建技术中去，“小波”有很多优点，比如它的分解多尺度的特性，它也可以分离出图像的高频和低频信息量等等[4]。

本文主要研究多帧图像的超分辨率图像重建，主要步骤为：运动估计、插值处理、图像重建。采用频率Vandewalle配准方法[5]，将处理过的低分辨率图像序列，映射到一幅高分辨率网格中去，由于在高分辨率网格上的分布不是均匀的，所以通过插值来得到一幅均匀分布的单帧图像，然后将小波变换和迭代方法[6]结合起来进行图像重建，在迭代过程中对高频子带采用图像融合技术[7]进行处理，以获得信息量增加的高频子带，再结合原始图像进行反复迭代，直到收敛到最优解为止。最后采用峰值信噪比来进行实验分析，结果表明重建图像很好的保持了图像原有的细节特征，加之多帧图像的超分辨率图像重建可利用的图像信息量丰富，所以重建图像有很好的峰值信噪比。

2 超分辨图像重建的数学模型

2.1 降质模型

超分辨率图像重建问题是一个严重病态的逆问题，如果想要求解这个逆问题，就必须弄清楚图像的成像过程。图像在获取的过程中，存在很多因素会使得图像的质量降低，如光学系统的像差、大气扰动、散焦和噪声污染等。因此，建立精确的退化模型对图像的重建至关重要，精确的模型更加精确和全面的反应成像过程的物理过程。

图1 低分辨率图像

首先，假设待重建的高分辨率图像的大小为L1N1×L2N2，表示成矢量的形式为f=[f1，f2，…，fN]T，N=L1N1×L2N2，f是理想的未经过降质的高分辨率图像，水平方向和垂直方向的降采样因子为L1和L2，由观测模型所获得的l帧低分辨率图像gk=[gk，1，gk，2，…，gk，M]T，k= 1，2，…，l，大小为N=L1×L2，由上图可以看出低分辨图像的降质模型为：

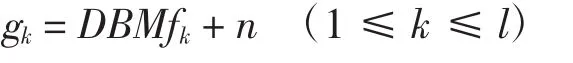
其中，D为形变矩阵，B为模糊矩阵，M为降采样矩阵，n为噪声。

本文中将采用上式的等价模型[8]：

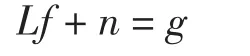
其中，矩阵L表示从高分辨率图像f到低分辨率图像g过程中的运动、模糊与下采样处理。采用文献[8]中的矩阵模型，矩阵L=Lx⊗Ly，“⊗”代表张量积，Lx与Ly代表水平和垂直方向的循环矩阵。矩阵L的第一行可以表示为。其中，前个元素为，最后个元素为非零元。

本文中结合小波方法中把当作小波低通分解矩阵，采用[9]中构造的相应的小波低通重构矩阵Ld，小波高通水平、垂直、对角线方向的分解矩阵H1，H2，H3，小波高通水平、垂直、对角线方向的重构矩显然满足因此，对任意的f，有f=LdLf+

2.2 重建模型

由上述模型可以看出超分辨率重建的模型就是降质过程的逆过程，大多数超分辨率重建的过程分为三个方面：运动估计（图像配准）、插值和重建。大体流程如下：

图2 重建过程

2.2.1 运动估计（Motion Estimation）

随着肿瘤治愈率明显提高，治疗时首要考虑的因素往往是平衡疗效与如何减少其治疗的毒性，尤其是儿童。在肿瘤的治疗中，心脏损伤是患者长期生存较严重的迟发性不良反应，而在引发心脏损伤的因素中，纵隔放疗和蒽环类药物的化疗是发生心脏疾病的最高危险因素，患者在初期可能无明显症状，但这种心脏毒性通常在治疗结束5-10年后方表现出来，并且心衰一旦发生，目前尚无有效救治手段。

对于图像重建技术来说，运动估计是实现图像超分辨率重建的基础，在图像处理领域占据着十分重要的地位，精准的运动估计对图像的重建效果有着明显的改善和影响。多帧图像的超分辨率重建技术就是利用一系列低分辨率图像之间的微小差异所包含的非冗余信息来提高图像的分辨率。所以，图像重建技术首先要得到低分辨率图像帧与帧间的运动信息，即低分辨率图像之间的偏移关系，求出几帧图像在同一位置时的位置差，通过分析，估计出相对位置参数，然后将各帧图像配准到同一坐标系。这样所有的低分辨率图像帧上的像素就映射到同一共同的参考帧上，然后再进行操作重建图像。可见，精准的运动估计对于图像重建技术来说至关重要，关系到重建图像的质量优劣。

本文采用的是基于频域的图像配准方法，该算法的配准精度比较高，采用频率域算法来估计运动参数，图像的运动可用包含水平、垂直和旋转角度的函数来表示，假设参考图像为f1（x），而f1（x）经过平移和旋转之后的图像为f2（x）：

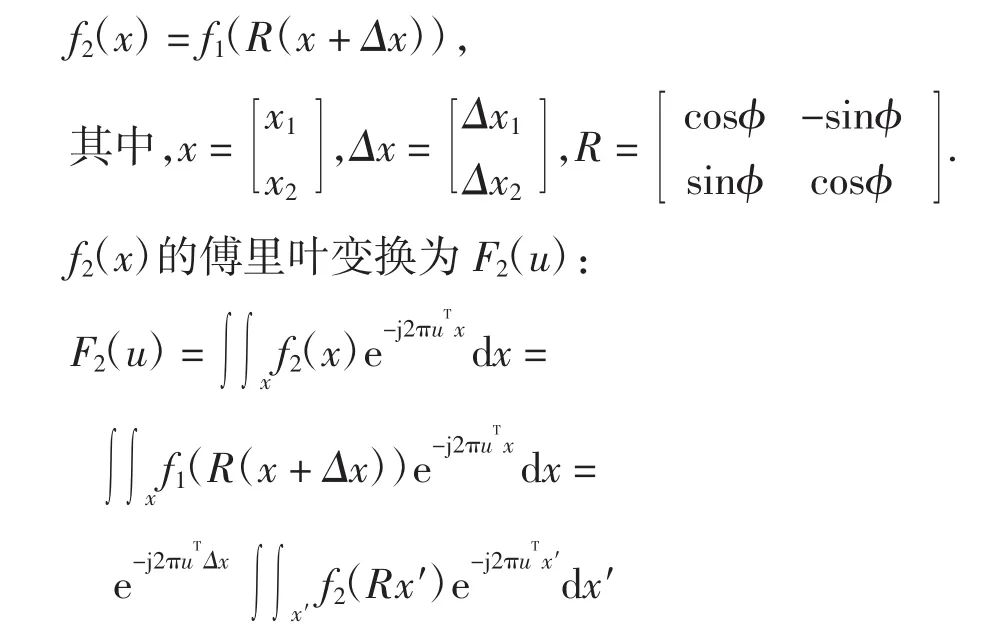
其中，x′=x+Δx，做变换x″=Rx′，则它们的振幅可表示为：

（1）旋转估计

为了更好的利用频域幅值的这种关系估计旋转角度，定义以下一个旋转角度为的函数：

（2）平移估计

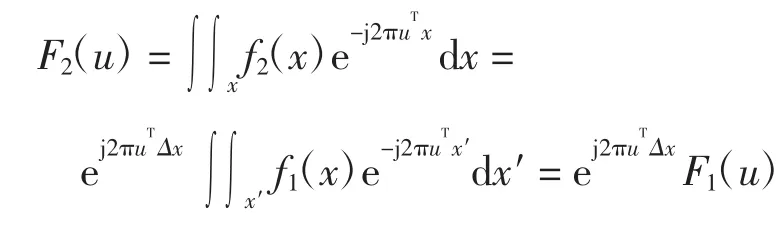
图像在平面内的移动可通过频率域中的一个线性相位移动来表示，相位差为∠（F2（u）/F1（u）），它是u的线性函数，平移参数Δx可以通过计算相位差的斜率2πΔx，为了减少对噪声的敏感度，可通过最小二乘法来拟合相位差平面的斜率。频域Vandewalle方法的鲁棒性很强，而且抗干扰能力很好，可以消除图像的混叠信息。

2.2.2 插值（Interpolation）

在图像序列经过运动估计之后，就要进行插值和重建；单帧图像则是直接进行插值和重建。插值是图像重建根本的环节，就是将运动估计后的低分辨图像的像素点投影到一个高分辨率网格上，这时，得到的图像往往是非均匀分布的，需要通过插值使其成为均匀分布的高分辨率图像[10]。

3 阈值去噪

一般来说，现实中的信号都是带噪信号，在对图像信号进一步分析之前，需要将有效的信号提取出来。信号在生成和传输过程中，常常受到很多噪声的干扰而使得质量变差，因此有目的地从测量数据过程中获取有用的信息，即进行去噪，就成为许多分析过程中的一个重要的步骤。

本文采用小波阈值去噪方法[11]对图像进行处理。即对小波分解后的各层系数中大于和小于某阈值的系数分别处理，然后对处理完的小波系数再进行小波变换，重构出经过去噪后的图像。

图2 重建过程

4 算法的提出

本文的算法先将低分辨率图像序列进行运动配准，采用频率Vandewalle配准方法，将处理过的低分辨率图像序列，映射到一幅高分辨率网格中去，由于在高分辨率网格上的分布不是均匀的，所以通过插值来得到一幅均匀分布的单帧图像，然后重建处理过的单帧图像，从而得到分辨率增加的图像。具体步骤如下：

第一步：经过简单处理得到可以使用的参考帧图像g，对一系列低分辨率图像相对于参考帧进行运动配准，首先，为了使图像得以对称，通过加塔基窗口得到窗口函数fLR，m，LR代表低分辨率，m代表第m幅低分辨率图像，将所有低分辨率图像进行傅里叶变换得到FLR，m，计算每幅待配准图像fm（m=2，3，…，M），关于参考图像f1的旋转角度：计算图像的极坐标（r，θ），对于任意角度α，计算相应的[5]中定义的旋转角度hm（α），hm（α）每隔0.1°计算一次，然后在选定的区间内寻找h1（α）和hm（α）的相关情况，找到满足条件的旋转角度。然后进行平移参数配准，计算待配准图像fm（m= 2，3，…，M）和参考图像f1的相位差，然后计算相位差斜率Δx，并以此为未知数，列出平面线性方程，并用最小二乘法得到方程的解作为平移参数Δxm。

第二步：在运动估计之后，将配准后的图像映射到高分辨率网格上，采用非均匀空域样本内插法，得到一幅均匀分布的高分辨率图像f0，作为以下步骤的初始估计。

第三步：对得到的高分辨图像我们再进行进一步地去噪去模糊，即对插值后的图像f0进行小波变换，计算Lf0，H1f0，H2f0，H3f0。将低分辨率图像g进行一级分解，得到低频子带S0和三个方向的高频子带即H1g，H2g，H3g。然后将高频子带H1g，H2g，H3g分别当作低频部分，相应的高频部分全部置零进行逆变换得到分辨率增加一倍的高频子带S1，S2，S3。

图像融合即将H1f0，H2f0，H3f0与S1，S2，S3进行融合。得到相应的高频子带S1′=tH1f0+（1-t）S1，S2′= tH2f0+（1-t）S2，S3′=tH3f0+（1-t）S3，t为权衡系数。

将处理过的高频子带进行上述小波去噪处理。再将原始图像当作低频部分结合融合后的高频部分进行小波逆变换得到超分辨率重建图像f1。

5 实验分析

为了说明本文算法在超分辨率图像重建上的优越性，我们采用插值方法、迭代反投影法[13]、稳健性重建方法[14]及本文的方法分别进行图像重建。选用峰值信噪比PSNR作为图像重建质量的客观评价标准。关于PSNR的具体表达如下[12]：

其中f（i，j）为原图像，fˆ（i，j）为重建图像，N×N为原图像尺寸。PSNR越大时，图像的质量越好。

实验1：实验选用512×512的Lena.jpg图像作为原始图像。首先进行下采样，得到256×256的低分辨率图像，并且以此作为参考帧，对参考帧行平移和旋转，可以得到包括参考帧在内的一系列低分辨率图像，本文选用4帧256×256的低分辨率图像作为重建的依据，按照上述方法进行重建，并依次选用非均匀内插法、迭代反投影方法、稳健性重建方法同本文的方法进行比较。实验结果如图4所示：

图4 算法比较

实验2：选用256×256的cameraman.jpg图像作为原始图像。首先进行下采样，得到128×128的低分辨率图像，并且以此作为参考帧，对参考帧进行平移和旋转，可以得到包括参考帧在内的一系列低分辨率图像，本文选用4帧128×128的低分辨率图像作为重建的依据，按照上述方法进行重建，并依次选用非均匀内插法、迭代反投影方法、稳健性重建方法同本文的方法进行比较。实验结果如图5所示：

实验结果表明，本文总结的基于小波的超分辨率图像重建算法，在多帧图像的超分辨率图像重建中，有很一定的优势，在一定程度上避免了图像模糊和边缘锯齿现象，图像的重建质量从视觉上有很好的效果，而对于客观的评价标准峰值信噪比而言，本文的方法和几种经典的重建算法相比较，提高了峰值信噪比。而同单帧图像的超分辨率图像重建相比较，当实验条件相同，我们可以看出多帧图像的超分辨率图像重建无论是从视觉效果还是从峰值信噪比对的结果而言，都有一定的优势，这是因为待重建的多帧低分辨率图像包含的信息量大，可以利用的信息量比单帧多，重建的效果自然会增强。

图4 算法比较

表1 Lena图像和cameraman图像的重建结果的PSNR值单位（dB）

6 结束语

超分辨重建技术自产生以来发展迅速，随着图像处理技术的日益推广，该技术越来越成为图像处理领域研究的热点，在几十年的时间里，无论是国外还是国内研究领域里都取得了重要的研究成果，超分辨重建技术有很重要的研究意义和实用价值。本文介绍的多帧图像重建方法在配准时候采用了Vandewalle配准方法并结合了小波和迭代方法的优势来重建图像，从而得到了分辨率提高的图像，并且图像很好的保持了图像的原有特征，也达到了很好的峰值信噪比。

［1］ 张良培，沈焕锋，张洪艳，袁强强.图像超分辨率重建[M].北京：科学出版社，2012.8.

［2］ 孙涛.光学遥感影像复原与超分辨率重建[M].北京：国防工业出版社，2012.7.

［3］ 王会鹏.多帧图像超分辨率重建算法研究[D].河南：解放军信息工程大学，2010.4.

［4］ 唐晓初.小波分析及其应用 [M].重庆：重庆大学出版社，2005.

［5］ Patrick Vandewalle，Sabine Susstrunk，Martin Vetterli.A Frequency Domain Approach to Registration of Aliased Images with Application to Super-resolution[J].Applied Signal Processing.2006，4：1-14.

［6］ 何进荣.基于加权范数迭代算法的总变差正则化图像复原方法：[D].武汉：武汉理工大学，2009.

［7］ 敬忠良，肖刚，李振华.图像融合理论与应用[M].北京；高等教育出版社，2007.10.

［8］ Raymond，H.Chan.Tony，F.Wavelet Algorithms for High-Resolution Image Reconstruction[J].SIAM J.SCI.Comput. Vol.24（2003）：1408-1432.

［9］ Hongjiu T，Xinjian T，Jian L，et al.Super-resolution Remote Sensing Image Processing Algorithm Based on Wavelet Transform and Interpolation[J].Proceedings of SPIE，2003，4898：259-263.

［10］唐磊.多帧图像超分辨率重建算法研究[D].浙江：浙江大学，2011.1.

［11］张明.图像超分辨率重建和插值算法研究[D].北京：中国科学技术大学，2010.5.

［12］张兰.多帧图像超分辨率重建关键技术研究 [D].天津：天津理工大学，2010.12.

［13］A.Rav-Acha，A.Zomet and S.Peleg，Robust Super-Resolution[J].Proceedings international conference on computer vision and pattern，recognition（CVPR），2001.Vol.I，pp.645-650.

Research on Multi-frame Images Super-resolution Reconstruction

WANG Jing，WU Ai-di
（School of Science，Tianjin University of Technology and Education，Tianjin，300222，China）

Multi-frame super-resolution image reconstruction refers to image processing which produce high resolution image from a set of distortion，blurring and down-sampling images.This technique fuses these low resolution sequences at pixel level to achieve a high resolution image.The steps are divided into:motion estimation，interpolation processing，image reconstruction.We apply the Vandewalle registration method to estimate motion parameter，then map to a high-resolution grid by interpolation.At last，the algorithm combined with the wavelet and iteration to reconstruct the super-resolution image.At the same time，we applied the method of wavelet threshold de-noising.The experiment results show that this algorithm improves the resolution and PSNR.It is a useful method of Super-resolution image reconstruction.

Super-resolution reconstruction；Motion estimation；Interpolation；Wavelet transform；Threshold de-noising

T

A

2095－0926（2014）04－0001－04

2014-00-00

天津市应用基础及前沿技术研究计划项目（12JCYBJC10600）

王 静（1988—），女，硕士研究生；吴爱弟（1963—），男，教授，硕士生导师，研究方向为图像处理、地震信号等.