基于Delphi的螺旋锥齿轮齿廓实体建模关键算法研究

王英杰，赵 巍，胡德计，潘 鑫

（天津职业技术师范大学天津市高速切削与精密加工重点实验室，天津 300222）

基于Delphi的螺旋锥齿轮齿廓实体建模关键算法研究

王英杰，赵 巍，胡德计，潘 鑫

（天津职业技术师范大学天津市高速切削与精密加工重点实验室，天津 300222）

根据成形法铣削螺旋锥齿轮切齿原理，推导出螺旋锥齿轮齿槽曲面的一元四次方程，通过求解一元四次方程得到齿槽上的关键点。为在Delphi+OpenGL环境下，利用所求得的关键点完成齿坯模型的建立，为仿真铣削过程的建立提供数据点。本文对比了在Delphi和Matlab下求解一元四次方程的不同，同时验证了本文算法的正确性。

一元四次方程；关键点；Delphi+OpenGL；Matlab

螺旋锥齿轮因其传动具有承载高、重叠系数大、传动平稳、传动效率高、噪声低以及安装误差对其的影响减小等特点，广泛应用于矿山、石油、煤矿机械、机床、铁路机车等机械工程领域。但作为一种局部点接触的不完全共轭的齿轮副，设计和加工过程非常复杂。在正式生产前往往需要通过调整、试切来初步验证所使用的加工调整参数的合理性，延长了生产周期、增加了生产成本、造成资源的浪费。采用虚拟仿真将很好地解决上述问题，然而目前对于锥齿轮的建模主要是在现有的商业工程软件基础上进行二次开发，在三维软件中，通过齿面方程得到齿面上的离散点，最后拟合成螺旋锥齿轮曲面，这种开发方式需要高昂的商业工程软件支持，不具备自主知识产权而且重用性差，一旦改变参数就必须从头开始。本文即针对上述问题，利用Delphi+OpenGL面向对象的开发软件，基于半滚切法加工的齿轮，建立了推导弧齿锥齿轮齿廓曲面关键点的一元四次方程，并在Delphi里求解其关键点。为实体建模奠定基础。

1 锥齿轮齿坯结构及参数确定

基于成形法加工的大轮，建立弧齿锥齿轮齿廓曲面关键点的方程，刀具、机床和工件的坐标系如图1所示。

1）在机床坐标系0M-xMyMzM下的背锥面方程：

2）在机床坐标系0M-xMyMzM下的面锥方程：

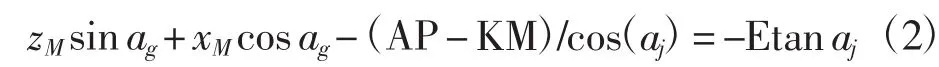
其中：KM为齿面宽，aj为节锥角。

3）内外刀面在0M-xMyMzM坐标系下方程：

H、V分别为刀盘中心到机床坐标原点的水平距离和垂直距离，a1为外刀齿形角，a2为内刀齿形角，R为刀具的公称半径，W为刀错距。

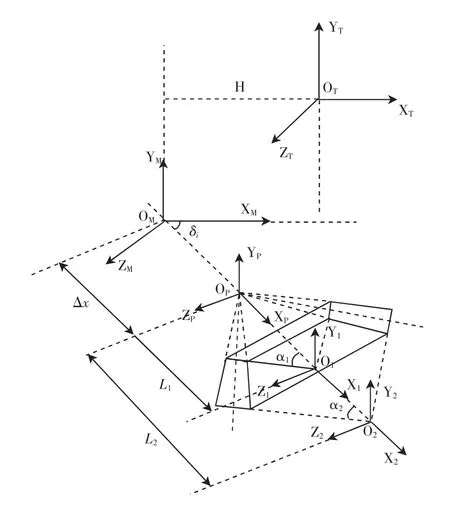
图1 切齿坐标系

4）求出交点

分别将方程（1）、（2）与（3）联立求出背锥、面锥与内（外）刀面的交点，即为一个一元四次方程，简记为：

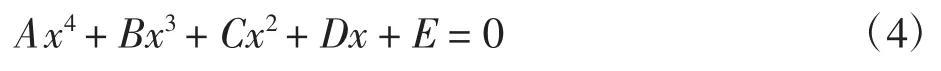
2 Delphi下求解一元四次方程

求解一元四次方程有数值迭代法求解和解析法求解两类方法，数值迭代法需要对区间进行搜索，计算量比较大也比较浪费时间[1]。解析法求解一般有两种方法，分别是笛卡尔算法[2]和费拉里解法[3-5]。通过比较计算精度和稳定性，本文采用费拉里解法。在Delphi下编写求解一元四次方程的程序，并通过离散点数，最终可以得到齿槽上一系列的点，通过建立点的数据结构，实现对齿坯的实体建模。

首先将一元四次方程两边同时除以最高项系数，然后移项得

式中：y是一参数，不论取什么值，（6）式总成立。特别地，若所取值使等式右边关于的二次三项式也能变成一个完全平方式，则对式（6）两边同时开方可以得到次数较低的方程。为使（6）式右边关于的二次三项式也能变成一个完全平方式，使它的判别式为0，即

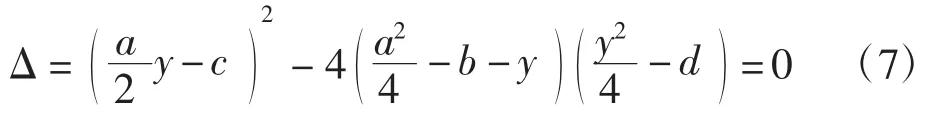
这是一个关于y的一元三次方程，利用一元三次方程的求根公式解出值，代入式（6）后两边开方，即可将四次方程降次成为一元二次方程，再通过一元二次方程的求根公式求解，最终能解出此一元四次方程的四个根，再根据系统需要对根进行取舍。Delphi下求解根流程图如图2所示。

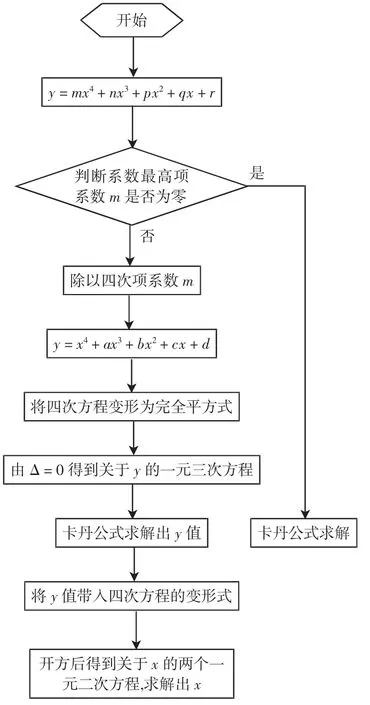
图2 求解过程流程图

3 实验验证

通过运行程序可以解出一元四次方程的解，由于每个齿槽有4条线组成，分别是内外刀面与面锥和根锥的交线，在 Delphi下求得的交点坐标为（1.90989236825379e+2，-3.48033964838081e+1，-1.67596083394905e+1）。本文在每条交线上取20个离散点。在Matlab里解非线性方程组的方法通常是牛顿迭代法，需要初值。结果表明，不论初值多少，在机床坐标系下求得的交点均为（1.909912e+2，-3.47978e+ 1，-1.67460e+1），与Delphi里求解结果一致，即验证了在Delphi下求解的正确性。表1列出2种算法的计算结果。

表1 Matlab与Delphi求得交点分析

求出齿槽上的关键点后，建立点链表和辅助链表的数据结构，通过三角片的连接原理和机床刀具的调整参数（表2）最终完成齿坯的实体造型如图3所示。

表2 加工调整参数

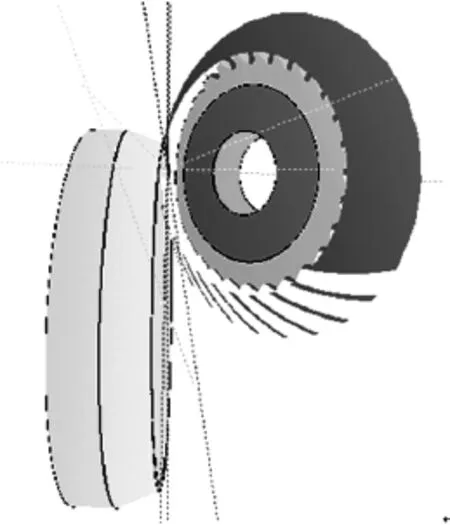
图3 大轮与刀盘啮合

4 结语

根据成形法加工螺旋锥齿轮的切齿原理，建立了螺旋锥齿轮及铣齿刀内、外刀面的数学模型，在Delphi下通过求解一元四次方程，得到了建模所需的关键坐标点，并在Matlab里验证了该方法的正确性，基于Delphi+Opengl建立了仿真铣削的界面和仿真模型，实现了仿真切削，为后续的螺旋锥齿轮数字化加工奠定了坚实的基础。

［1］ 周志宏.一元四次方程2种根式求解算法的精度分析[J].长江大学学报（自然科学版），2009，6（3）：5-6.

［2］ 郭敏.一元四次方程公式解的求根溯源[J].数学之友，2011（12）：72-73.

［3］ 智海章.一元四次方程求解方法的思考与研究[J].甘肃高师学报，2001，6（2）：25-26.

［4］ 王跃华.浅谈三次方程与四次方程的解法[J].沈阳大学学报，2010，22（6）：8-10.

［5］ 马飞龙，胡德计，赵巍，等.弧齿锥齿轮成形法数控加工仿真建模与实现技术[J].机械工程与自动化，2011，（1）：20-22.

［6］ 李兆文，王勇，万金领.基于实际切齿方法的弧齿锥齿轮建模与仿真[J].组合机床与自动化加工技术，2008（6）：26-30.

［7］ 熊越东，王太勇，张威.螺旋锥齿轮数控加工参数转换计算方法[J].组合机床与自动化加工技术，2006（8）：5-9.

［8］ 丁撼，阿达依·谢尔亚孜旦.新型螺旋锥齿轮数控铣齿机的结构模型设计[J].组合机床与自动化加工技术，2013（10）：28-31.

［9］ 胡芳芳，吴国星，胡德计.数控系统圆柱车削的虚拟仿真实现[J].现代制造工程，2005，（8）：17-19.

［10］王太勇，邢元，李琳，等.螺旋锥齿轮虚拟加工过程算法[J].天津大学学报，2012，45（2）：116-120.

The study on the key algorithm of spiral bevel gear tooth profile modeling based on Delphi

WANG Ying-jie，ZHAO Wei，HU De-ji，PAN Xin
（Tianjin Key Laboratory of High Speed Cutting&Precision Machining，Tianjin University of Technology and Education Tianjin300222，China）

According to the principle of forming milling spiral bevel gear teeth，a yuan quartic equation of the spiral bevel gear tooth surface is derived and the key points on the tooth are got by solving a quartic equation.The Gear blank model is established by using the obtained key points Under Delphi+OpenGL circumstance，providing data points for the establishment of the simulation of milling process.This article compares the differences to solve equation of four times a yuan under Delphi and Matlab，at the same time，the algorithm in this paper proved to be correct.

a yuan quartic equation；key points；Delphi+OpenGL；Matlab

TH132；TP311

A

2095－0926（2014）04－0001－04

2014-07-10

天津市应用基础及前沿技术研究计划项目：跨平台数控系统运行机理及结构研究（10JCYBJC06900）

王英杰（1988—），女，河南商丘人，硕士，研究方向为螺旋锥齿轮仿真算法；赵 巍（1976—），女，副教授，博士，研究方向为数字化制造。