水声信号的非线性建模与预测方法
孙 妍, 李亚安, 陈 晓, 戴 淼, 高文娟
水声信号的非线性建模与预测方法
孙 妍, 李亚安, 陈 晓, 戴 淼, 高文娟
(西北工业大学 航海学院, 陕西 西安, 710072)
对水声信号尤其是混响干扰和背景噪声的预测和滤波, 是水下目标信号检测的基础, 在非平稳、非高斯、非线性水声信号处理中具有重要应用。本文利用最小二乘估计和Volterra级数理论, 分别对水声信号建立预测模型并进行一步及多步预测, 通过分析预测结果, 选取最优预测参数。仿真结果表明, 基于奇异值分解的Volterra级数模型的预测相对误差较最小二乘估计小一个数量级, 预测结果更加逼近真实值。
水声信号; 混响干扰; Volterra级数; 最小二乘估计; 非线性建模; 多步预测
0 引言
近年来, 随着水声研究的重点向近岸浅海海域的转移, 有关海洋噪声的非线性研究越来越受到人们的高度重视。水声信号处理是信号处理的一大分支[1]。由于水声信号的高度复杂性, 以传统信号处理理论为基础的水声信号处理, 立足于水声信号的平稳性、随机性和线性, 而忽略了水声信号的非平稳性和非线性。Volterra级数是泛函数的一种[2], 多年众多学者的理论研究和工程实践表明, Volterra级数模型是一种工程应用价值很高的非线性模型, 可应用于大多数非线性系统。
本文首先采用经典的线性方法建立系统的线性模型, 然后重点采用Volterra级数模型的方法对系统进行非线性建模, 并在此基础上对目标信号分别实现一步及多步预测, 并对预测结果进行比较分析。预测结果表明, Volterra级数模型结合了水声信号的线性及非线性特性, 预测效果优于最小二乘估计。
1 线性模型
线性预测是根据已有的数据序列, 按照线性函数来计算未来某一时刻的数据信号的数学方法。最常见的表示形式为

线性最小二乘估计, 是以误差的平方和最小为准则, 根据观测数据线性模型中位置参数的一种基本参数估计法。1794年, 德国数学家C.F.高斯在解决行星轨道预测问题上首先提出最小二乘法。它的基本思路是选择估计量使预测值与真实值之差的平方和达到最小。线性最小二乘法是应用最广泛的参数估计方法。本文采用最小二乘估计作为线性预测的模型。


利用得到的核函数及测试样本序列, 进行线性最小二乘法预测。
2 非线性模型
2.1 Volterra滤波器模型
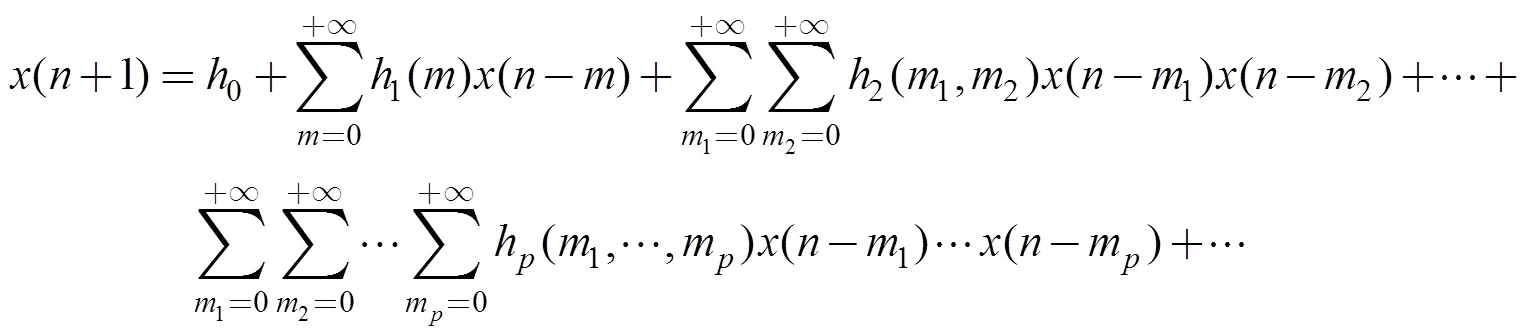

由式(5)得, Volterra滤波器实质是非线性FIR滤波器, 滤波器的输入信号矢量和核函数分别为
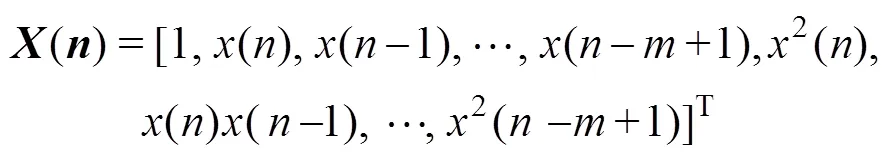

则式(3)可表示为

2.2 奇异值分解Volterra滤波器模型
在此基础上, 本文采用奇异值分解Volterra滤波器[4-5](SVD-Volterra)的方法计算非线性系统的核函数。

其中:
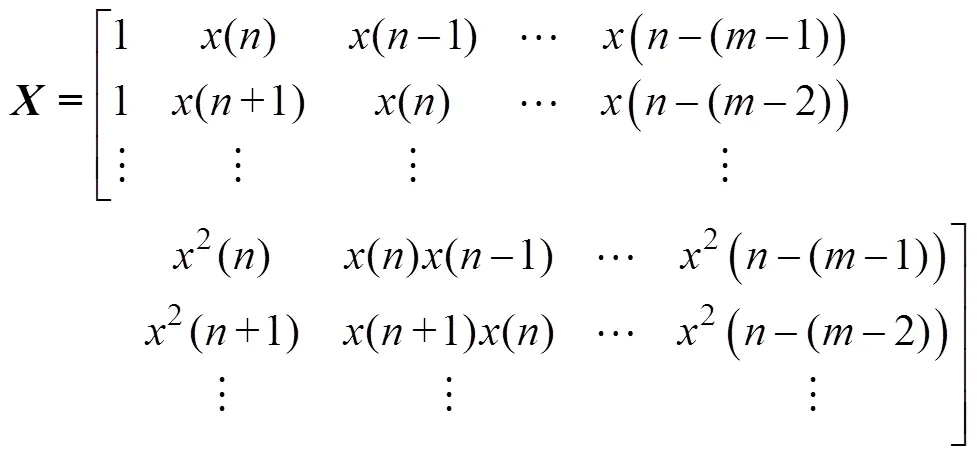
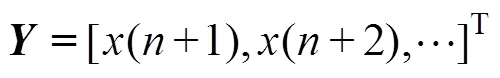
。并有, , 当时, 矩阵方程(9)有最小二乘解。根据奇异值分解, 存在正交矩阵, 使得


3 预测原理

设输入矢量为
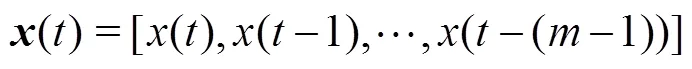

3.1 Volterra滤波器一步预测
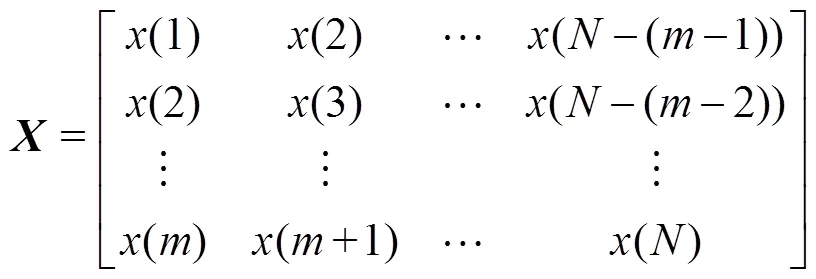



3.2 Volterra滤波器多步预测
4 预测仿真结果与讨论
本文选用Lorenz信号、Duffing信号及海洋试验数据作为仿真信号, 以Lorenz和Duffing信号训练预测模型, 在此基础上, 展开基于线性最小二乘法、非线性奇异值分解Volterra自适应滤波的一步及多步预测。
首先对仿真信号进行归一化处理

然后取仿真信号的1000个点进行预测模型的训练, 取该仿真信号中不同于训练序列样本的500个点作为测试序列, 并以预测相对误差作为评判标准。定义相对误差为

表1、2分别为Lorenz序列和Duffing序列不同预测步长的相对误差比较。对于相同信号, 3阶Volterra自适应滤波器的预测性能要优于线性最小二乘估计。对于不同的信号, 3阶Volterra自适应滤波器的有效预测步长也不尽相同。在此基础上, 本文选择3阶Volterra自适应滤波器, 实现对海洋噪声和舰船噪声的一步及多步预测, 多步预测的有效步长均可达25步, 预测结果见图3和图4。

图1 Lorenz流x分量预测

图2 Duffing流x分量预测
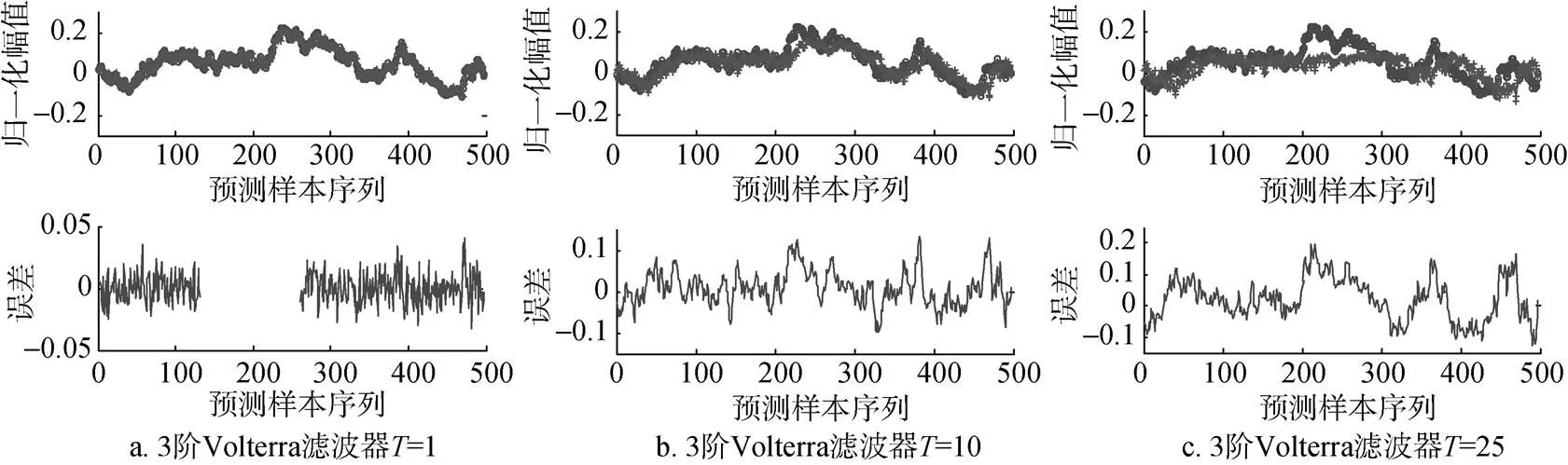
图3 海洋噪声Volterra预测

图4 舰船噪声Volterra预测

表1 Lorenz序列预测相对误差

表2 Duffing序列预测相对误差
5 结束语
本文选用Volterra级数和线性最小二乘的方法, 分别对混沌序列建立预测模型, 在Volterra级数建模中采用基于奇异值分解的自适应算法, 在此基础上展开一步预测和多步预测的研究。仿真结果表明, 采用基于奇异值分解的Volterra自适应滤波器实现多步预测, 结果优于线性最小二乘估计, 原因在于Volterra级数不仅包含了信号的线性特性, 更包含了信号的非线性特性, 能够更逼近真实的信号。此外, 对于不同的信号, Volterra自适应滤波器的有效预测步长也不尽相同。这对利用Volterra自适应滤波器开展针对水声信号, 尤其是混响干扰和背景噪声的滤波及预测研究, 及如何提高预测模型精度和有效预测步长的研究, 具有重要意义。本文的创新点在于, 通过比较线性最小二乘估计和非线性Volterra级数模型的预测结果, 说明Volterra级数模型能够结合水声信号的线性及非线性特性, 具有更好的预测性能, 对水声信号处理的进一步研究提供理论依据。
[1] 朱昀. 水声信号非线性分析方法研究[D]. 西安: 西北工业大学, 2002.
[2] 张秀梅. Volterra滤波器的自适应算法研究[D]. 杭州: 杭州电子科技大学, 2009.
[3] 张家树, 肖先赐. 混沌时间序列的Volterra自适应预测[J]. 物理学报, 2000, 49(3): 403-408.
Zhang Jia-shu, Xiao Xian-ci. Predicting Low-Dimensional Chaotic Time Series Using Volterra Adaptive Filter[J]. Acta Physica Sinca, 2000, 49(3): 403-408.
[4] 陆振波, 蔡志明, 姜可宇. 基于奇异值分解的混沌时间序列Volterra预测[J]. 武汉理工大学学报, 2007, 31(4): 672-675.
Lu Zhen-Bo, Cai Zhi-ming, Jiang Ke-yu. Prediction of Chaotic Time Series Using Singular Value Decomposition Volterra Filter[J]. Journal of Wuhan University of Technology, 2007, 31(4): 672-675.
[5] 房媛媛, 李亚安, 崔琳, 等. 基于Volterra级数的自适应水声信号预测方法研究[J]. 兵工学报, 2013, 34(9): 1173-1179.
Fang Yuan-yuan, Li Ya-an, Cui Lin, et al. Research on Pr- ediction of Underwater Acoustic Signals Based on Volt- erra Adaptive Filter[J]. Acat Armamentarii, 2013, 34(9): 1173-1179.
[6] 雷亚辉, 宋春云, 丁士圻. 基于Volterra自适应滤波的水中混响非线性预测[J]. 哈尔滨工程大学学报, 2007, 28(10): 1127-1130.
Lei Ya-hui, Song Chun-yun, Ding Shi-qi. Nonlinear Pred- iction of Underwater Reverberation Based on a Volterra Adaptive Filter[J]. Journal of Harbin Engineering Univ- ersity, 2007, 28(10): 1127-1130.
[7] Boné R, Crucianu M. Multi-step-ahead Prediction with Neural Networks a Review[J]. Approches Connexionnistes en Sciences éconemiques et en Gestion, 2002(11): 97-106.
(责任编辑: 杨力军)
Nonlinear Modeling and Prediction of Underwater Acoustic Signal
SUN YanLI Ya-anCHEN XiaoDAI MiaoGAO Wen-juan
(School of Marine Science and Technology, Northwestern Polytechnical University, Xi′an 710072, China)
The prediction and filtering of underwater acoustic signals, especially of reverberation interference and background noise, lay the foundation of underwater target signal detection and processing of non-stationary, non-Gaussian and nonlinear underwater acoustic signals. In this paper, based on the linear theory of least square estimation and the Volterra series theory, two prediction models of target signal are established to conduct one-step and multi-step predictions. Thus, the optimal prediction parameters are obtained by comparing and analyzing the prediction results. Simulations show that the prediction model based on singular value decomposition of Volterra series achieves more accurate results in predicting the underwater acoustic signal, and its relative error of prediction is one-order of magnitude smaller, compared with the model based on least square estimation.
underwater acoustic signal; reverberation interference; Volterra series; least square estimation; nonlinear modeling; multi-step prediction
TB566; TN911.7
A
1673-1948(2014)05-0341-06
2014-04-10;
2014-07-02.
国家自然科学基金(51179157).
孙 妍(1987-), 女, 在读硕士, 主要研究方向为水声信号处理.
——信号处理

