航空发动机振动数据阶比分析应用研究

李国鸿

(中国飞行试验研究院，陕西西安710089)

航空发动机振动数据阶比分析应用研究

李国鸿

(中国飞行试验研究院，陕西西安710089)

试飞中发动机振动信号处理时，需获得各转子阶次谐波分量的准确幅值，以便对发动机振动进行评估和监视。针对该问题，对阶比分析技术在该领域的具体应用进行了研究，并给出了实现方法。该方法采用sinc函数插值的方法，将等时间间隔采样的离散数据序列转换为等角度采样的离散数据序列，随后对等角度采样后的数据序列进行快速傅里叶变换(FFT)和谐波分解，来获得信号阶次谱。分析结果表明，给出的实现方法消除了FFT分析的截断效应，提高了阶次谱分量幅值的分析精度。

航空发动机；截断效应；阶比分析；等角度采样；阶次谱

1 引言

目前，航空发动机振动信号处理，一般采用通用的基于FFT的频谱分析方法。但这种分析方法在执行过程中会引起频谱分析误差，且这些误差可用混叠现象、栏栅效应和截断效应三种现象来描述[1～5]。虽然混叠现象可通过采样前的抗混叠滤波消除，栏栅效应可通过提高信号采样率的方法保证，截断效应可通过加窗处理来尽可能消除，但由于目前一般的振动数据采集记录设备采用的都是等时间间隔采样方式，FFT分析数据块时长固定，分析频率分辨率不变，在航空发动机状态变化时，其主要特征分量由于截断效应带来的误差变化，不能同时兼顾各特征分量的截断误差。

阶比分析技术以旋转机械的转速而不是时间、频谱上的阶比而不是频率作为关注重点，因此一般阶比谱图上，信号的幅值或频率是旋转机械转轴频率阶次的函数。在旋转机械状态变化时，某一阶次的谐波成分就固定在一独立的谱线上，不随转速变化，避免了一般通用频谱分析中出现的谐波混叠效应[6～9]。此外，由于一般阶比分析技术都采用等角度采样[8～12]，理论上可完全消除各阶次谐波分量的截断效应，保证各阶次分量的截断误差。

航空发动机主要特征分量的频率为转子转频的倍数，这与旋转机械阶比分析中阶比的含义一致。同时考虑到阶比分析的优点，本文将结合目前试飞中航空发动机振动信号处理现状，对如何将阶比分析技术应用于航空发动机振动数据处理领域进行研究，以期进一步提高振动数据分析的能力和质量。

2 阶比分析理论

2.1 阶比定义

旋转机械振动时，通常关注的振动特征分量的振动频率为该旋转机械转速的倍数或分数，该倍数和分数就是阶比。振动分析中使用阶比，主要是因为转速与阶比的对应关系恒定。阶比与旋转机械转速的关系通常可用下式表示：

式中：f为频率，E为阶比，n为转速。

2.2 等角度采样

与一般振动信号采样不同，采用阶比分析时，被测振动信号要经过等角度增量的阶比采样变为角域离散序列，再经离散傅立叶变换到阶比域进行分析。同步采样后所得数据的采样单位，是每转的分数而不是每秒的分数。若再用这些数据进行傅里叶变换，得到的测试结果将是一种频率尺度类型的函数，以阶比而不是赫兹为增量。

对于平稳信号，若信号为整周期等角度采样，则每次采样截取的信号长度都等于振动信号周期的整数倍，且信号为等间隔采样。频谱分析时，分析谱线将落在振动信号的频率上，从而获得比较准确的频谱，以避免频谱泄漏和栅栏效应对频谱分析精度的影响。对于非平稳信号，整周期等角度采样可使信号在一定程度上变得平稳，可减弱频谱泄漏和栅栏效应对分析精度的影响。

3 阶比分析应用

目前，发动机试飞中所获得的发动机转速数据和振动数据，来自两个不同的数据采集记录系统。振动数据以等时间间隔采样方式获得，对其的分析主要依赖事后的二次处理。要开展针对性的阶比分析算法研究工作，必须考虑上述现状。

图1所示为充分考虑目前试飞中发动机振动数据分析现状，并根据实际应用需要，重点实现了整周期等角度采样的发动机振动数据阶比谱实现方法示意图。图中，n(n)为转速数据序列，a(n)为振动数据序列，ns(n)为时间同步后的转速数据序列，as(n)为时间同步后的振动数据序列，asb(n)为缓冲区振动数据序列，asb,rs(l)为完成了等角度重采样的振动数据序列，asb,rs,w(l)为完成了等角度重采样和数据截取后的振动数据序列，Asb,rs(m)为序列asb,rs,w(l)的复频谱，Asb,rs(m)为序列asb,rs,w(l)的谐波分解结果。

图1 发动机振动数据阶比谱实现方法示意图Fig.1 Order spectrum implementing method of aero-engine vibration

图中首先对n(n)和a(n)进行时间同步处理的主要原因，是n(n)和a(n)来自两个不同的数采系统，采样率不同且差别很大；对振动数据设置一个缓冲区，主要是为后续的FFT做准备，缓冲区大小除必须考虑FFT分析的块大小要求外，同时还要考虑重采样和截断的一些特殊要求。数据截取过程可通过对序列asb,rs(l)加矩形窗来实现。

3.1 重采样

选用sinc函数插值法实现等角度采样。设a(n)、as(n)的采样率为fs，需跟踪的转速信号频率为fn，则等角度重采样过程如式(2)所示：

asb(n)长度N与序列asb,rs(l)长度L之间的关系如式(3)所示：

设重采样过程中对频率为fn的正弦信号每周期采样点数为2M1，序列asb,rs,w(l)的长度为2M，则asb,rs(l)的采样率为：

M、M1、M2三者之间的关系如式(5)所示：

3.2 缓冲区长度

由于sinc(t) 函数是一个主瓣宽度为2、旁瓣宽度为1且迅速衰减的函数，而缓冲区振动数据长度固定，因此利用式(2)插值时，会在asb,rs(l)首、尾两端产生振荡效应。鉴于此，为保证重采样结果的准确性，采取了使缓冲区振动数据的时间长度大于asb,rs,w(l)的时间长度，然后在后续数据截取中所截取数据序列避开as,rs(l)首、尾两端振荡区的方法。实际应用中，N的取值可参照下式进行：

3.3 阶次谱

对asb,rs,w(l)实施常规发动机振动信号处理中的FFT和谐波分解操作，就可得到需要的阶次谱序列Asb,rs(m)。此时Asb,rs(m)的频率分辨率为fn/2M2，阶次分辨率为1/2M2，可用阶次范围为1/2M2～2M1-1。

4 仿真分析

4.1 sinc函数插值重采样

图2示出了某仿真信号重采样测试结果。可见，正如前文分析结果，利用sinc函数插值完成重采样，数据的首、尾两端有明显的振荡效应，且振幅迅速衰减(大约5个sinc(fs,at)函数的旁瓣宽度)，振荡波形与sinc函数类似；其余部分波形与重采样前的数据波形一致。

图3示出了不同采样率对仿真结果的影响。可见，重采样前信号采样率fs,a，对重采样后数据首、尾两端振荡效应的影响不同，fs,a越大影响越明显。

4.2 稳态阶次谱

仿真高低压转子频率分别为：fn,h=181.25 Hz，fn,l=60.00 Hz。仿真振动信号如式(7)所示：

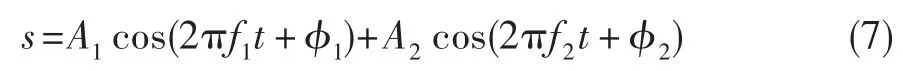
式中：A1=1，f1=fn,l，φ1=0，A2=2，f2=fn,h，φ2= 0.3π。fs=5000，振动仿真信号时长T=5 s。

仿真获得的低压、高压阶次谱如图4所示，常规FFT频谱如图5所示。对比两图可发现，由阶次谱获得的低压转子转速nl和高压转子转速nh基频分量的幅值误差，总体上明显小于由常规FFT频谱获得的基频分量的误差。此外，常规FFT频谱分析中FFT数据块大小对转子基频分量幅值误差的影响较大，且具有一定随机性；但M对由阶次谱获得的nl和nh基频分量幅值的影响有规律，即M越大误差越小。

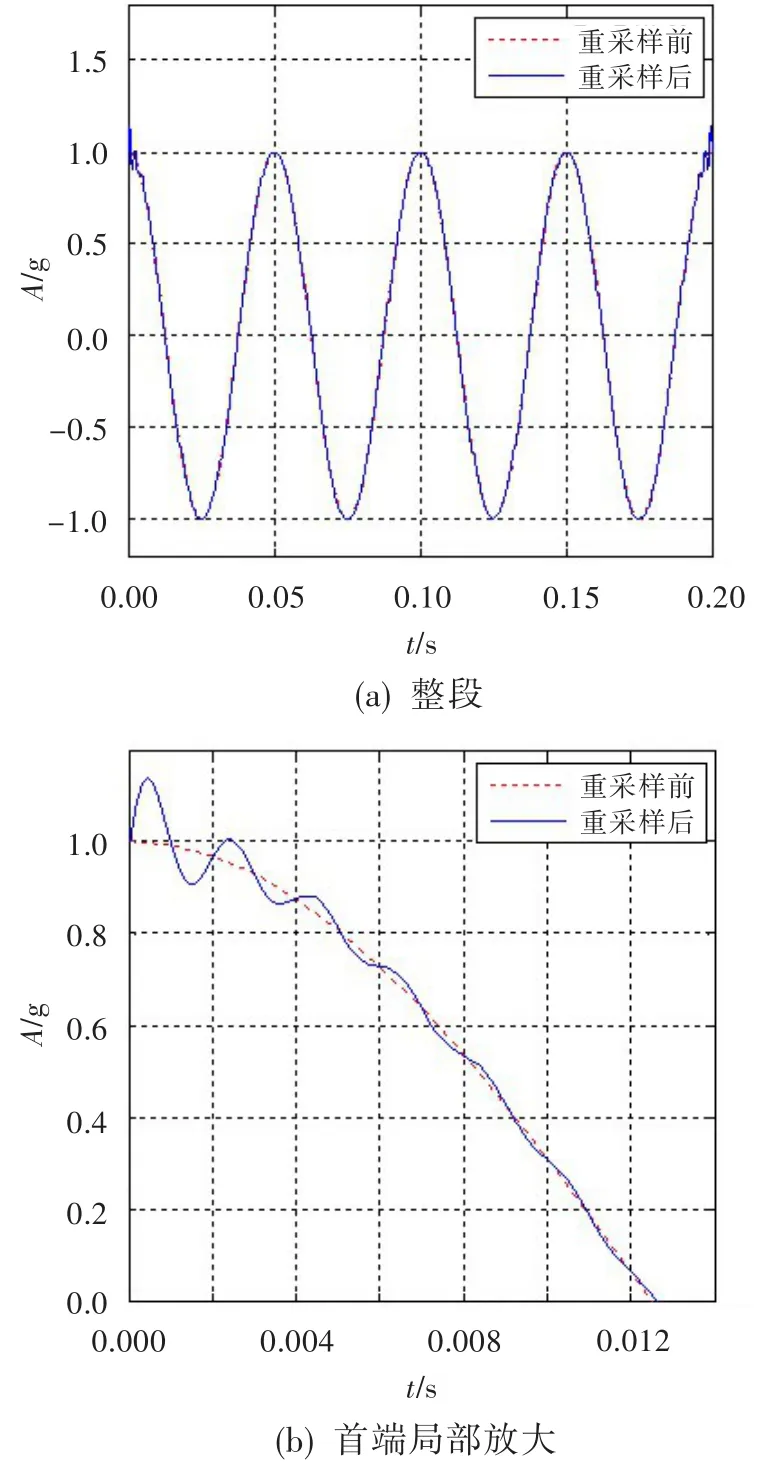
图2 某仿真信号重采样测试结果Fig.2 Test results of a simulating signal

图3 不同采样率对仿真结果的影响Fig.3 Effects of different sample rate on simulation results

5 实测数据分析

利用某涡扇发动机试飞中加装的加速度振动传感器记录的实测数据，对前文所述阶比分析算法进行进一步分析和验证。

5.1 稳态阶次谱

图6所示为某涡扇发动机某稳态高、低压阶次谱分析结果。可见，利用阶次谱可更清晰地分辨出发动机转子基频和倍频分量(低压转子阶次分别为2、3、6、11、17的振动分量，高压转子阶次分别为1、2、11的振动分量)。与常规的FFT频谱相比，由于阶次谱的横坐标为阶比，因此利用阶次谱识别高、低压转子基频和倍频分量时更直观。此外，由前文的分析可知，由阶次谱获得转子基频、倍频分量幅值的误差更小。

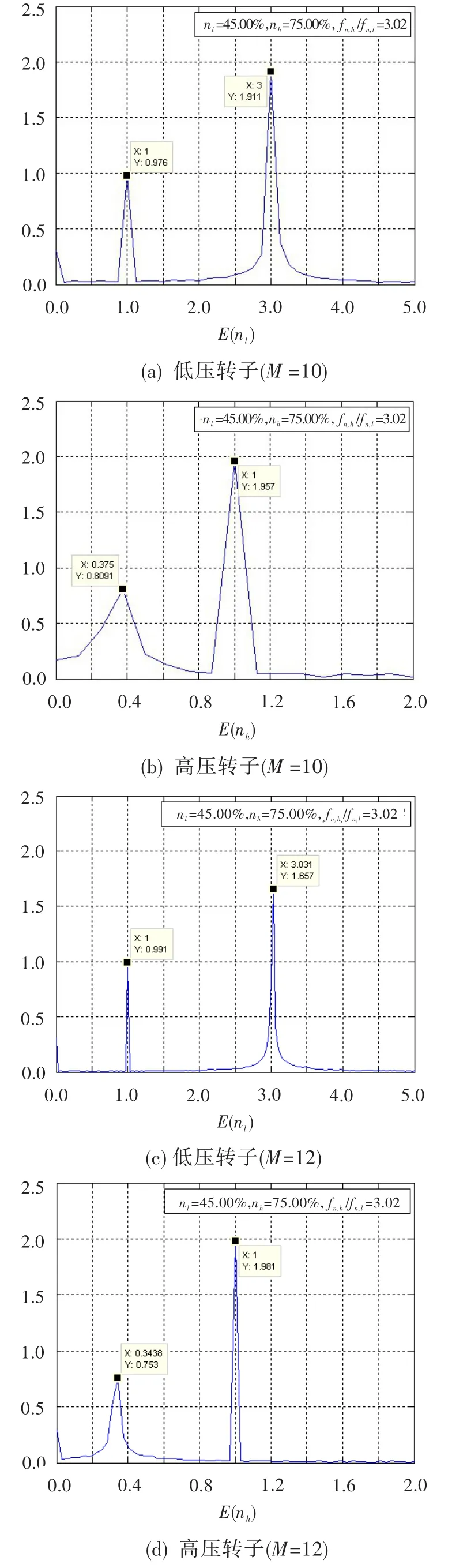
图4 稳态仿真数据阶次谱Fig.4 Order spectrum simulating results in stable state

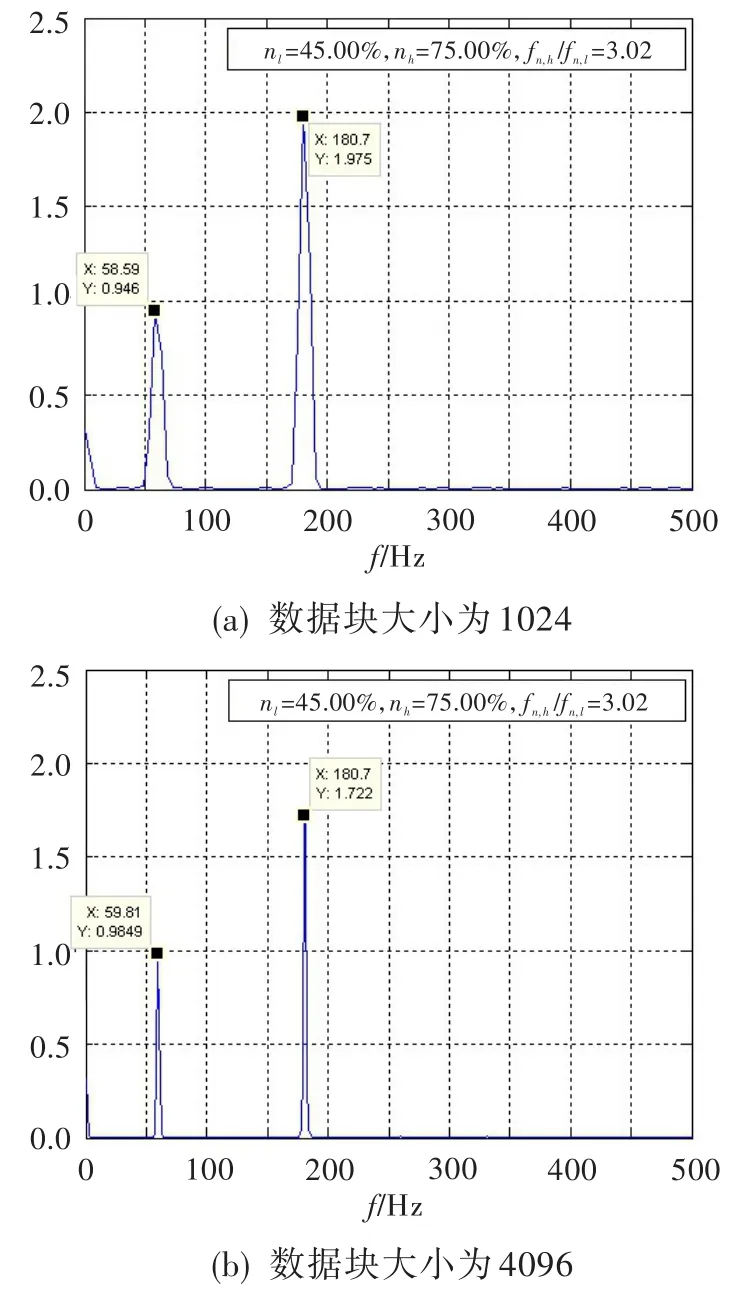
图5 稳态仿真数据常规FFT频谱Fig.5 FFT spectrum simulating results in stable state

5.2 过渡稳态阶次谱

图7所示为利用阶比分析方法，对某涡扇发动机某过渡态振动数据进行分析的高、低压转子阶次谱云图。可见，过渡态阶次谱可以很清楚地反映转子基频、倍频分量幅值随时间的变化。图7(a)中，对应时间历程曲线nl=41%、nh=74%的时刻(此时刻发动机转速比约为3)，nl的3倍频或nh的1倍频、nl的6倍频或nh的2倍频、nl的14倍频分量比较明显(在云图上显示为一条跟背景噪声明显区分的亮线)；其余时刻，nl的5倍频分量比较明显。与稳态阶次谱类似，利用过渡态阶次谱可更直观地识别过渡态高、低压转子基频和倍频分量的变化，且精度更高。

5.3 分量跟踪

图8所示为在5.2节基础上，对高、低压转子过渡态基频分量进行跟踪的结果。可见，通过阶次谱获得的高、低压转子基频分量在整个时间历程中的变化趋势，分别与高、低压转子转速的变化趋势类似。在相对时间35～50 s期间，有一个比较明显的增大，这与转子基频分量主要反映转子系统的不平衡量、一般情况下其幅值随发动机转速增大而增大的原理一致。

图6 某涡扇发动机稳态阶次谱Fig.6 Order spectrum of an aero-engine in stable state

图7 某涡扇发动机过渡态阶次谱Fig.7 Rotor order spectrum of an aero-engine in transition state

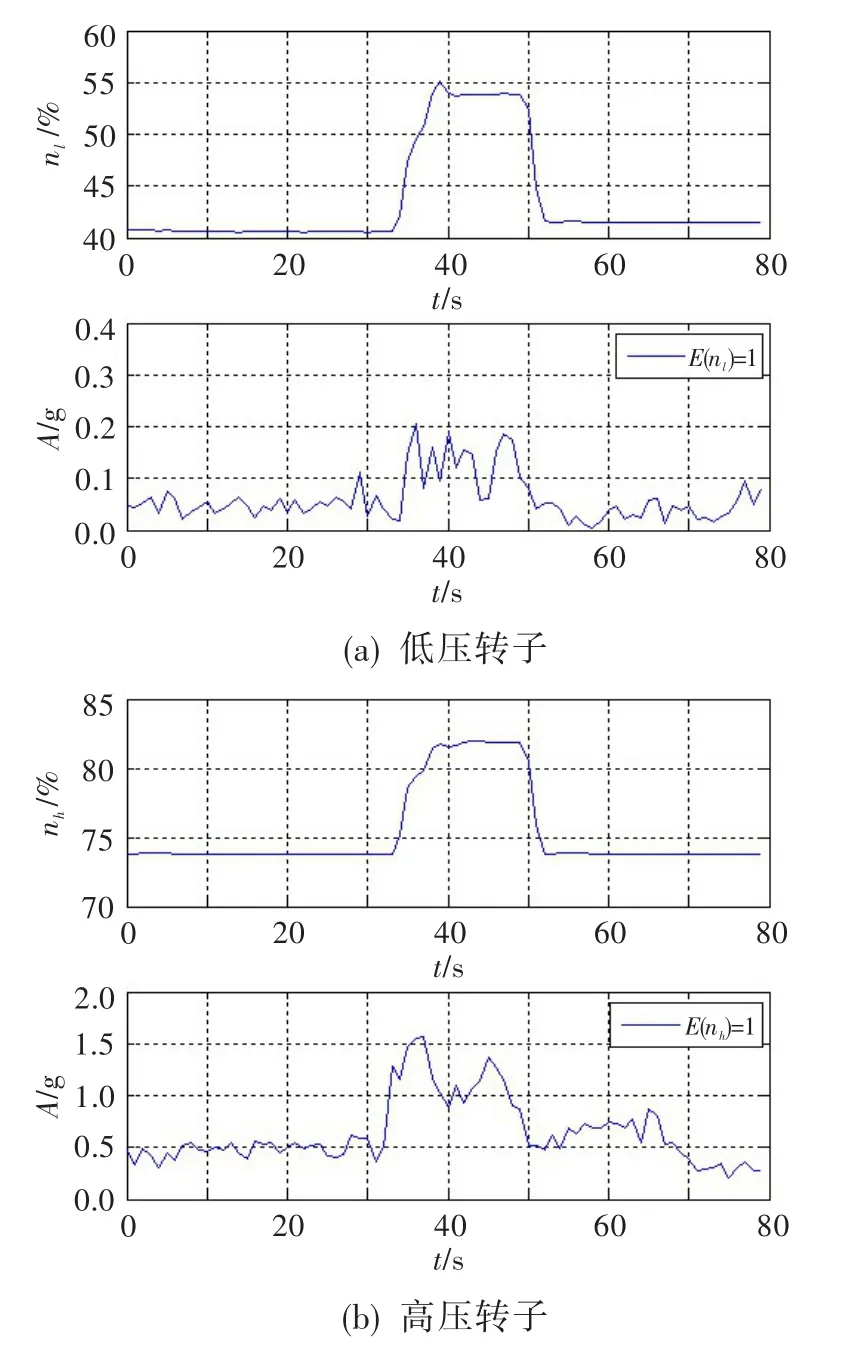
图8 某涡扇发动机过渡态转速与基频分量幅值的时间历程Fig.8 The relation between rotating speed and basic order amplitude of an aero-engine in transition state

与稳态阶次谱和过渡态阶次谱分析结果类似，利用阶比分析技术跟踪转子分量，所获得的分量幅值由于彻底消除了截断效应带来的误差，其分析误差更小，精度更高。

6 结论

(1)阶比分析方法由于采用了整周期等角度采样技术，理论上可彻底消除常规FFT频谱分析中的截断效应，提高所跟踪转子基频、倍频分量的精度。

(2)利用sinc函数插值的方法，可实现重采样前、后数据序列采样率之比为任意值的整周期等角度采样，但处理时必须注意重采样后数据序列首、尾两端的振荡效应。

(3)阶比分析中，M的取值对处理结果有一定影响，M取值越大，阶比谱分量的幅值误差就越小，但效率会下降。

(4)与常规FFT频谱相比，利用阶比谱诊断发动机振动故障时，高、低压转子的基频和倍频分量更容易识别，这主要是因为阶比与发动机高、低压转子转速之间存在着恒定的对应关系。

(5)利用阶比谱分析结果，可跟踪过渡态发动机转子基频、倍频振动分量，且所获得的振动分量的幅值误差，总体上要小于基于常规FFT的分量跟踪结果。

[1]胡广书.数字信号处理理论、算法与实现[M].2版.北京：清华大学出版社，2003.

[2]丁玉美，高西全.数字信号处理[M].2版.西安：西安电子科技大学出版社，2000.

[3]屈玉池，魏海涛，赵述元.动态信号处理中的问题及改进[J].飞行试验，2001，17(2)：5—10.

[4]李杭生，陈丹.频谱分析中窗函数的研究[J].微计算机信息，2008，24(1-4)：272—273.

[5]刘广臣，张惠安，贾爱宾.数字信号处理中的加窗问题研究[J].长沙大学学报，2003，17(4)：59—62.

[6]宋文健.阶比分析方法的研究[D].河北：燕山大学，2006.

[7]杨志坚，丁康，梁茜.基于频谱校正理论的阶比跟踪分析[J].机械工程学报，2009，45(12)：41—45.

[8]杨通强，郑海起，龚烈航，等.计算阶次分析中的采样率设置准则[J].中国工程机械学报，2011，9(1)：14—18.

[9]高艳，郑华文，陈永星.阶比跟踪中的惠特克插值[J].昆明理工大学学报(理工版)，2007，32(3)：30—34.

[10]汪伟，杨通强，王红，等.非稳态信号计算阶次分析中的重采样率研究[J].振动、测试与诊断，2009，29(3)：349—351.

[11]温政钢，栾军英.基于定点DSP的计算阶次跟踪研究[J].装甲兵工程学院学报，2010，24(4)：62—64.

[12]郭瑜，秦树人，汤宝平.基于分段重叠零相位滤波的阶比跟踪滤波法[J].振动工程学报，2003，16(4)：399—403.

Order Tracing Application Study on Aero-Engine Vibration Data Processing

LI Guo-hong
(Chinese Flight Test Establishment，Xi’an 710089，China)

While vibration data is processed in aero-engine flight tests,the accurate amplitude of the rotors is required for vibration analysis and monitor.In this paper,how to use order tracing technology to solve aero-engine vibration data processing problem in flight tests was studied carefully;moreover the realizable or⁃der tracing numerical algorithm was presented too.Sinc function interpolation method was used to get the sampling angles discrete data sequence from sampling time span.Then FFT and harmonic decomposition was complied on the new data sequence to obtain the signal order spectrum.The analysis results show that the presented method can avoid the truncation effect,and improve the accuracy of the order amplitude analysis.

aero-engine；truncation effect；order tracing；uniform angle sampling；order spectrum

V231.92

：A

：1672-2620(2014)04-0042-06

2013-09-19；

：2014-01-14

李国鸿(1977-)，男，陕西凤翔人，高级工程师，硕士，主要从事航空动力装置飞行试验相关的结构强度试飞，以及相关的发动机振动测试、振动数据分析等研究工作。