基于模糊控制交互式多模型粒子滤波的静电机动目标跟踪

付巍，郑宾

(中北大学 计算机与控制工程学院，山西 太原030051)

0 引言

静电探测技术是一种通过测量目标自身的静电场获取目标运动状态信息的探测技术［1］。基于静电探测技术的探测器具有被动式、反低空、反隐身的优势，可被应用于探测低空飞行的目标。目前已经设计出能够应用于探测空中目标的静电探测器主要有短路轴向式探测器［2］、电极扫描式探测器［3］、球形探测器［4］和旋转式三维静电探测器［5］等。这些探测器所得到的探测方程包含探测器与目标之间的相对距离和速度等真实信息，并且这些探测方程都是非线性的，探测数据中包含着非高斯分布的噪声，因此，需要利用目标跟踪算法根据静电探测器当前采样时刻的测量信息和前一个采样时刻的目标运动状态的预测值，估算出目标当前采样时刻的运动状态，以实现对机动目标的有效跟踪。

在机动目标跟踪中，目标经常有多种运动状态，单一模型的目标跟踪算法不能满足对机动目标跟踪性能的要求。交互式多模型算法假定目标的运动状态可用有限个运动模型描述，并为每个运动模型分配一个滤波算法和概率，根据当前采样时刻的测量信息在不同的运动模型之间进行交互和更新，实现对机动目标的跟踪［6］。交互式多模型算法对机动目标跟踪的效果主要依靠各运动模型概率和运动模型间的转换概率矩阵［7］。如果概率较大的运动模型与当前采样时刻目标的实际运动状态相一致，跟踪的误差就小，反之就大。交互式多模型算法的模型转换概率矩阵是先验矩阵，即在算法开始前就预先指定的，如果能够根据目标的实际运动状态情况实时调整模型转换概率矩阵每一列的值，使与目标当前运动状态最接近的运动模型在混合产生这一采样时刻的初始状态向量里占有更大的比重，交互式多模型算法将会更有效地实现对机动目标的跟踪。为此，提出一种基于模糊控制的交互式多模型算法，即利用模糊控制方法来实现对模型转换概率矩阵的实时调整，使与目标当前运动状态最接近的运动模型在混合产生这一采样时刻的初始状态向量里占有更大的比重。

为了在交互式多模型算法中实现对目标运动状态的更新，并解决探测方程非线性和探测数据含有非高斯噪声的问题，常采用粒子滤波算法。粒子滤波的效果在很大程度上取决于重要性密度函数的选取，重要性密度函数选择不好，常会导致滤波发散或较差的滤波效果［8］。为了提高粒子滤波算法的精度，减小算法更新时间，提出利用中心差分扩展卡尔曼滤波算法得出基本粒子滤波的建议分布函数，通过这个建议分布函数来代替基本粒子滤波算法的重要性密度函数，实现对目标运动状态的更新。

1 静电探测系统数学模型

静电探测器采用旋转式三维静电探测器，该探测器有x、y、z 3 个方向的感应电极。假设目标静电场的三维电场强度分量Ex、Ey、Ez，在感应电极上产生感应电量Qx、Qy、Qz，Qx、Qy、Qz随时间的变化率就是电流，因此，测量3 个方向上的感应电极的电流变化，就能够确定目标静电场的三维电场强度分量的变化，通过目标静电场的三维电场强度分量可以计算得到目标与静电探测器之间的方位角和俯仰角。

利用旋转式三维静电探测器探测飞行目标的方式如图1所示。当目标与探测器的距离较远，即距离大于目标尺寸的5 ～6 倍时，可以认为目标为点目标［9］。图1中探测器的架设高度为h，被探测目标的初始坐标为(x0，y0，z0)，并以沿x 轴、y 轴和z 轴的速度vx、vy、vz从P 点向探测器飞来。

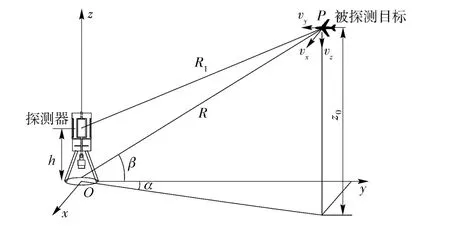
图1 旋转式三维静电探测器探测低空目标示意图Fig.1 Schematic diagram of the rotating three-dimensional electrostatic detector detecting a low-altitude target

在旋转式三维静电探测器3 个方向的感应电极上产生的电场强度的三维分量分别为

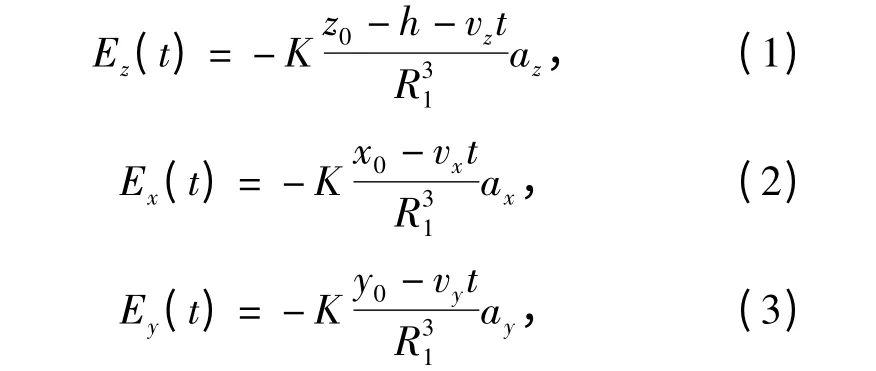
式中:ax，ay和az分别为沿x，y 和z 轴的单位方向向量;R1为目标距探测器电极的距离;K 为电场强度系数。

则旋转式三维静电探测器与目标之间的方位角

因为目标飞行高度z0比探测器架设高度h 大很多，所以R1≈R. 旋转式三维静电探测器与目标之间的俯仰角

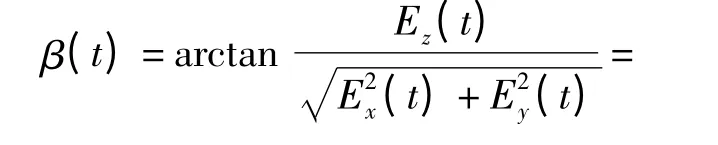
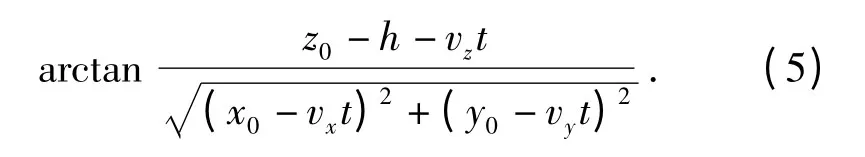
旋转式三维静电探测器在每一个采样时刻可以同时得到当前时刻目标与静电探测器之间的方位角和俯仰角等角度信息。利用探测器测得的角度信息，结合目标跟踪算法就能够估算出目标当前的运动参数，如位置、速度等信息，实现对机动目标的跟踪。

2 基于模糊控制的交互式多模型粒子滤波(FIMMPF)算法

2.1 交互式多模型粒子滤波(IMMPF)算法及改进

假设动态系统状态空间模型为

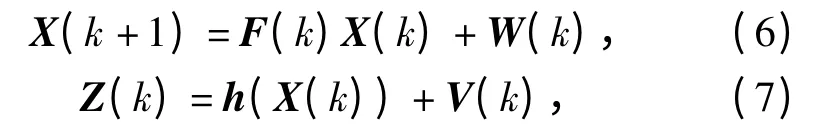
交互式多模型算法的核心思想是假定目标的运动状态可用有限个运动模型描述，各运动模型之间的转换概率由如下一阶马尔可夫链约束:

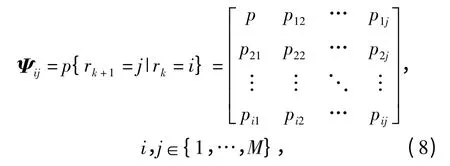
式中:Ψij表示运动模型转换概率矩阵;rk表示机动运动目标在第k 个采样时刻所属的运动模型，其值域为{1，…，M}，M 表示系统包含运动模型的数目。

在第k 个采样时刻系统处于第rk=i 个运动模型的概率记为

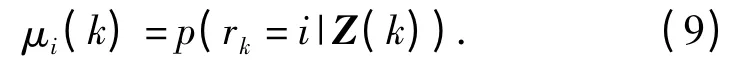
利用中心差分扩展卡尔曼滤波算法对基本粒子滤波的建议分布进行构造，形成改进的IMMPF 算法，其运算流程如下:

1)计算运动模型混合概率。计算运动模型混合概率的公式为

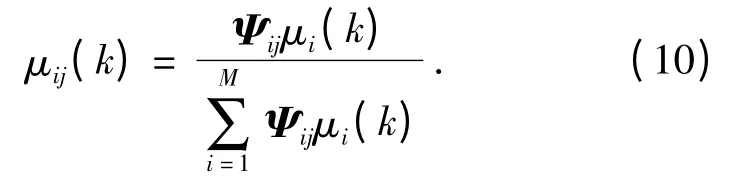
2)计算基于运动模型的混合状态初值和混合初始状态估计误差协方差矩阵。设粒子点的个数为N，而运动模型个数为M，这些粒子点在第k 个采样时刻第i 个运动模型产生的状态估计向量和状态估计误差协方差矩阵可以表示为Xni(k)，Pni(k)，其中:i=1，…，M;n=1，…，N.

混合所有运动模型的相应的粒子点，则第j 个运动模型的混合状态初值及初始状态估计协方差矩阵为

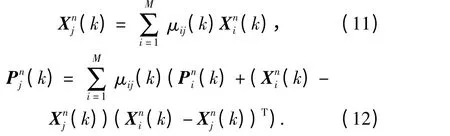
3)用中心差分扩展卡尔曼滤波算法进行滤波。利用第k+1 采样时刻的测量数据Z(k+1)，对每个运动模型中的N 个粒子点，通过中心差分扩展卡尔曼滤波算法进行滤波，得到第k+1 个采样时刻的每一个粒子点的运动状态向量的更新值，包括更新的状态向量(k+1)，更新的状态向量估计的误差协方差矩阵(k+1)，似然函数Lnj(k +1)和每个粒子点的权重(k+1).

采用中心差分扩展卡尔曼滤波算法进行建议分布的构造，其步骤如下:

预测状态向量

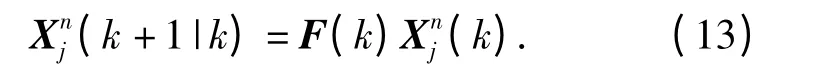
预测协方差矩阵

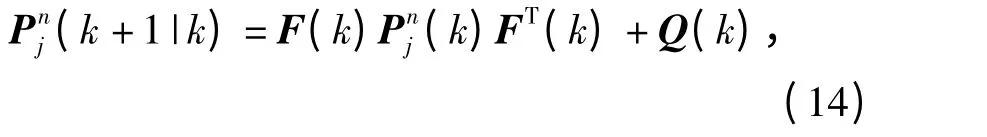
式中:Q(k)为状态方程噪声的协方差矩阵。

残差协方差矩阵:

令

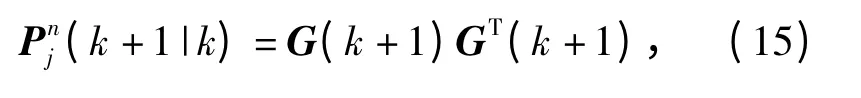
则

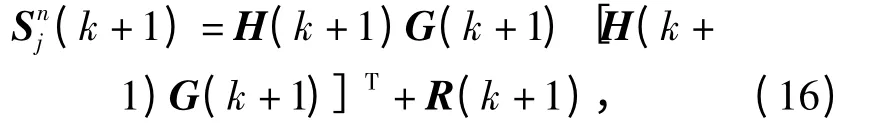
式中:H(k)为观测方程状态转移矩阵;R(k)为观测方程噪声的协方差矩阵。

令

应用中心差分理论

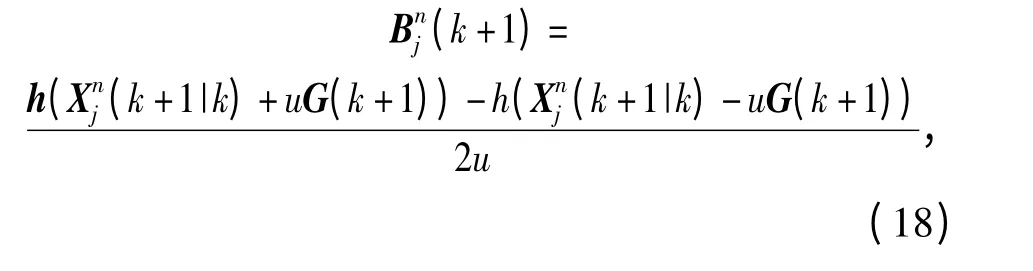
式中u 表示中心差分的步长，则

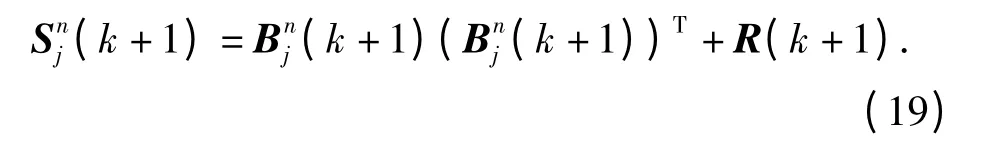
滤波增益矩阵

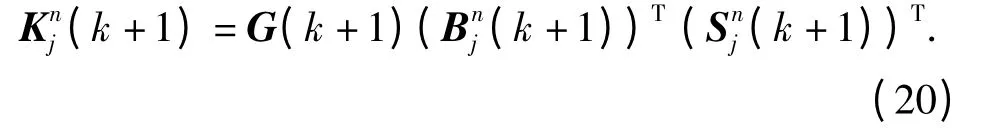
滤波输出

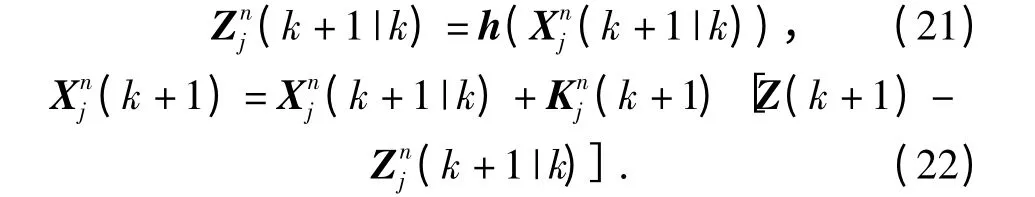
误差协方差矩阵

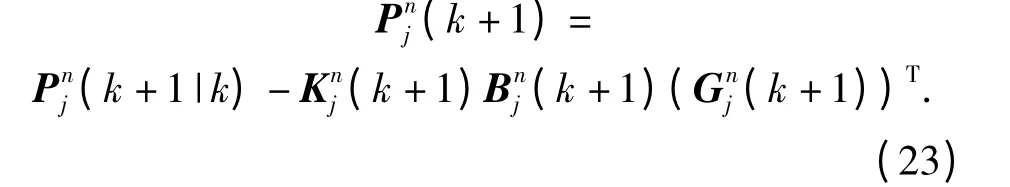
计算每个粒子点在第k +1 个采样时刻第j 个运动模型的的似然函数:

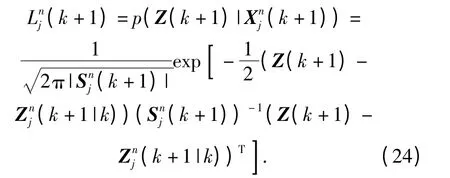
通过公式wnj(k +1)=wnj(k)Lnj(k +1)计算权重，规则化权重

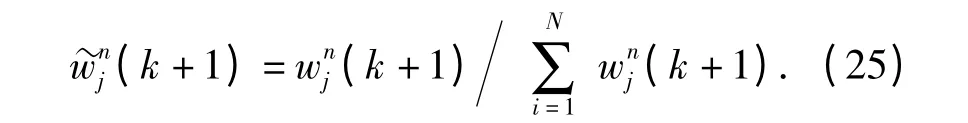
4)更新每个运动模型的概率。

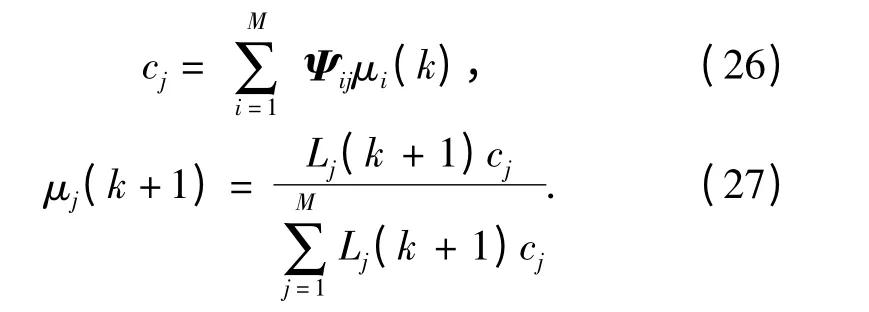
5)加权求和。

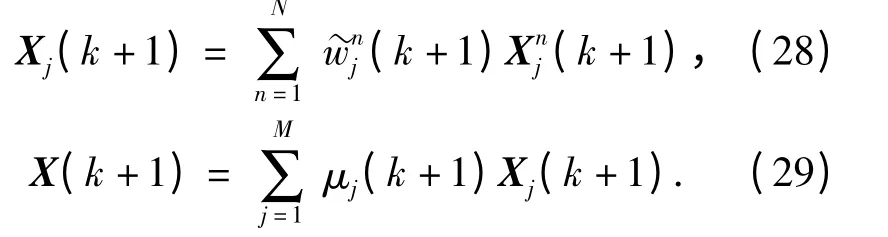
在IMMPF 的第3)步计算过程中，利用中心差分扩展卡尔曼滤波算法对基本粒子滤波进行建议分布构造，实现对目标运动状态的更新，可大幅减小状态更新时间，且跟踪精度较高。

2.2 模糊推理机

从(24)式可以看出，各个运动模型概率的更新是用运动模型的似然函数计算得到的，而似然函数表示的是在当前采样时刻运动模型与目标实际运动的一致性程度。因此，运动模型概率也同样反映了在当前采样时刻运动模型与目标实际运动的一致性程度，模型概率越大，表示这个运动模型与目标实际运动越接近。用新更新得到的运动模型概率μi(k+1)作为模糊推理机的输入，根据模糊推理机的结果计算第k+1 个采样时刻运动模型间的转换概率矩阵Ψij(k +1)，能够反映当前采样时刻运动模型与目标实际运动的一致性程度。

为了避免出现隶属函数值过小的情况，同时考虑到计算各个运动模型的似然函数采用的是高斯概率密度函数的形式，因此，采用高斯形隶属函数计算每个模型概率的隶属度。运动模型概率的隶属函数如图2所示。图2中的NB(负大)、PB(正大)、ZO(0)、PS(正小)、PM(正中)表示模糊子集，利用运动模型概率所属的模糊子集可以确定模型转换概率矩阵Ψij.

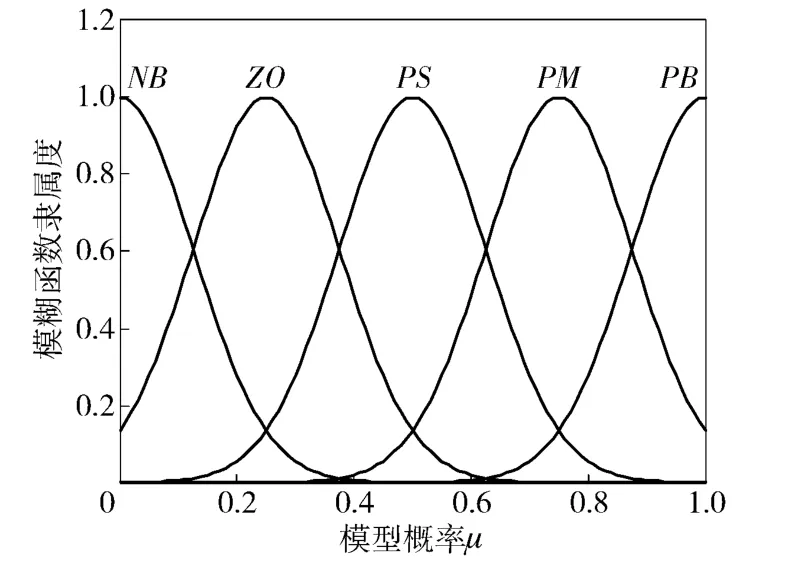
图2 运动模型概率的隶属函数Fig.2 Membership functions of motion model probability

模型转换概率矩阵Ψij是M×M 维矩阵，它能够混合产生所有运动模型的模型混合概率。为了实现根据目标实际运动情况实时调整模型转换概率矩阵，设计模糊推理机的运行规则，设Ψmij表示第m 条规则下模型转换概率矩阵。假定运动模型个数等于4，则模糊推理机的运行规则如下所示。

规则0:如果μ1是ZO 并且μ2是ZO 并且μ3是ZO 并且μ4是ZO，那么Ψij=Ψ0ij.

规则1:如果μ1是PS 并且μ2是NB 并且μ3是NB 并且μ4是NB，那么Ψij=Ψ1ij.

规则2:如果μ2是PS 并且μ1是NB 并且μ3是NB 并且μ4是NB，那么Ψij=Ψ2ij.

规则3:如果μ3是PS 并且μ1是NB 并且μ2是NB 并且μ4是NB，那么Ψij=Ψ3ij.

规则4:如果μ4是PS 并且μ1是NB 并且μ2是NB 并且μ3是NB，那么Ψij=

当模糊推理机判断模型概率属于以上5 条规则之一时，模型转换概率矩阵Ψij就等于相应的，对的定义如下:

式中:

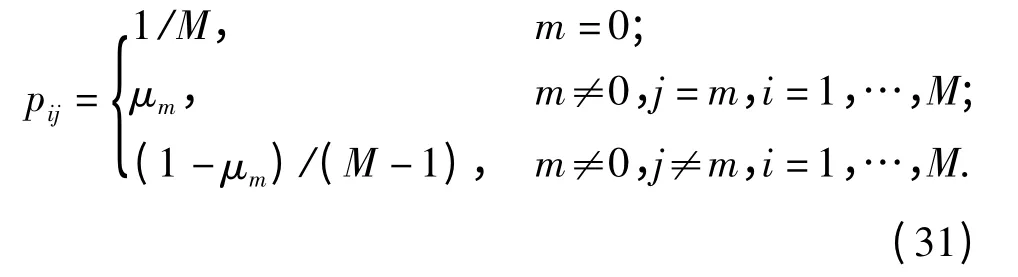
当模糊推理机判断模型概率不属于以上5 条规则之一时，模型转换概率矩阵Ψij由加权平均法决定:

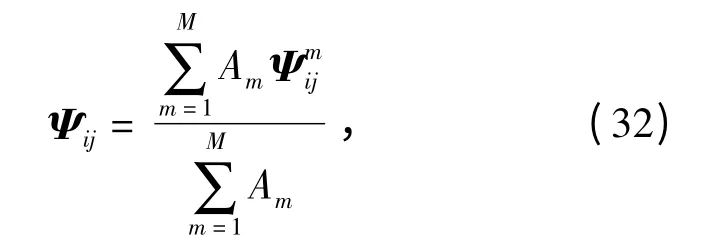
式中:Am表示第m 条模糊规则在总输出中所占的权重，按取小法得出Am的值。

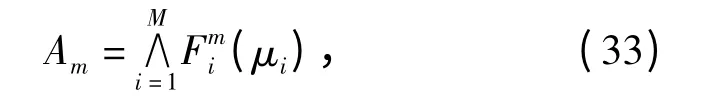
式中:∧表示取小的符号;Fmi(μi)表示输入到模糊推理机中的模型概率的隶属函数值。

3 仿真实例

选择单个机动运动的跟踪问题进行仿真实验，将FIMMPF 与文献［10］IMMPF、文献［11］IMMUPF进行仿真比较，观察这3 种目标跟踪算法在精度和实时性方面的性能。

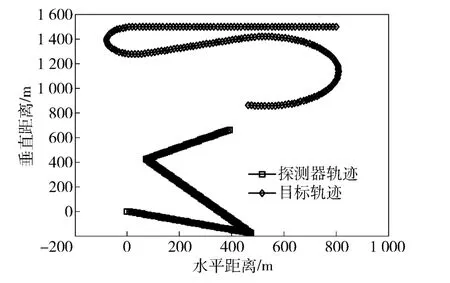
图3 机动目标跟踪场景示意图Fig.3 Schematic diagram of maneuvering target tracking

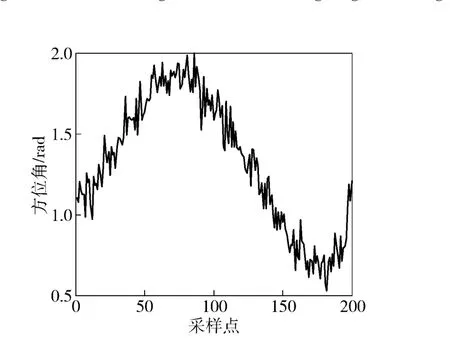
图4 测量得到的方位角变化曲线Fig.4 Changing curve of measured azimuth

算法参数设置如下:对于交互式多模型算法，主要是运动模型的选择和设置，在本次仿真实验中，选择3 种运动模型，3 种运动模型的角速度分别设置为ω1=0 rad/s，ω2=0.115 rad/s，ω3= -0.046 rad/s.3 种运动模型的初始模型概率为μ1=μ2=μ3=1/3;模型间的初始转换概率矩阵都是Ψij=［0.33，0.33，0.33;0.33，0.33，0.33;0.33，0.33，0.33］. 设置4 个模糊子集，这4 个模糊子集分别为NB(负大)、ZO(0)、PS(正小)、PB(正大)，它们的中心分别为0，1/3，2/3，1;模糊函数选择高斯形隶属函数。在改进的粒子滤波算法中，应用了中心差分扩展卡尔曼滤波算法，取中心差分的步长无迹粒子滤波算法的粒子数取为N =100. 分别用3 种目标跟踪算法对其进行跟踪，蒙特卡罗仿真次数为100，将它们的相对距离误差和相对速度误差曲线进行比较，如图5～图8所示。

图9～图11 分别是用3 种算法跟踪时模型概率的变化曲线图。

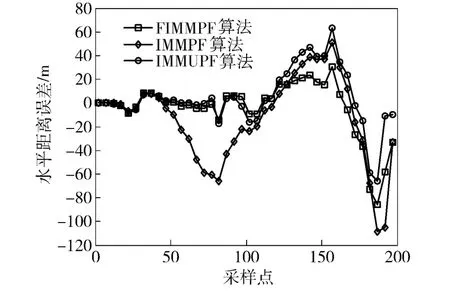
图5 目标与探测器水平相对距离误差Fig.5 Horizontal relative distance estimation error between target and detector

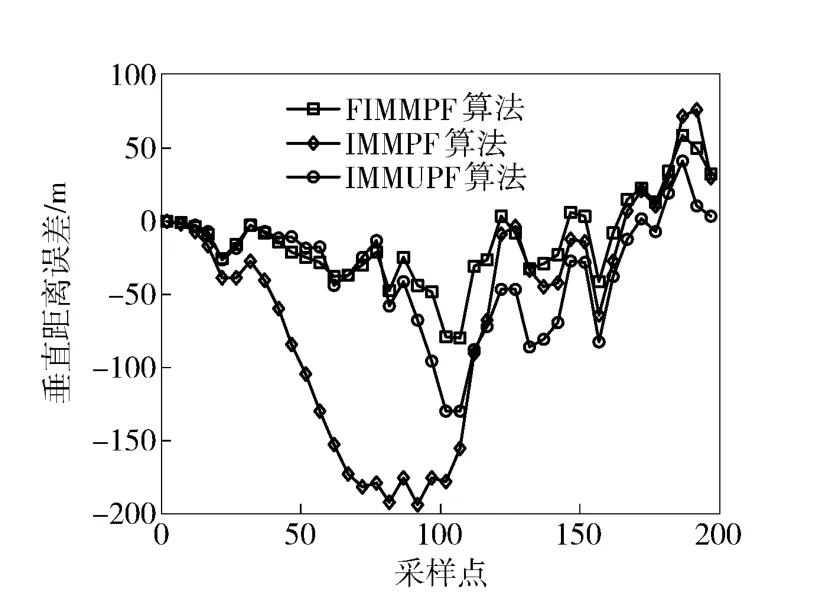
图6 目标与探测器垂直相对距离误差Fig.6 Veritcal relative distance estimation error between target and detector

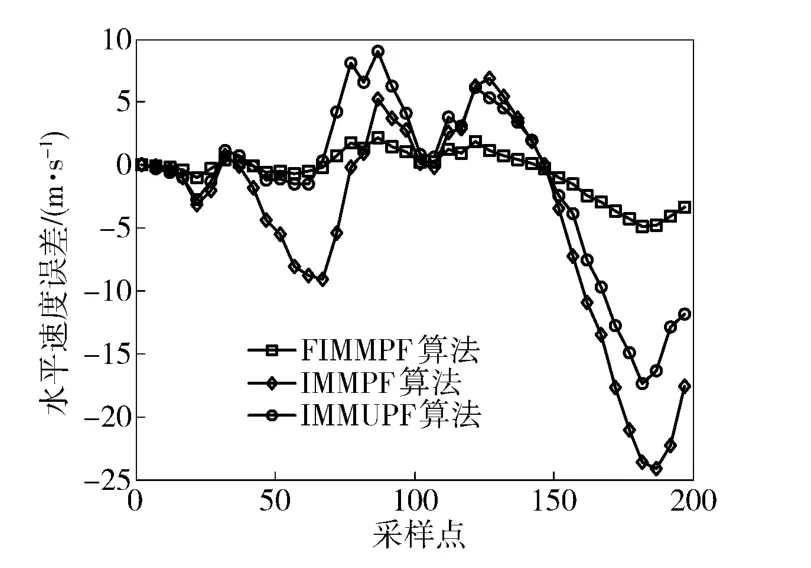
图7 目标与探测器水平相对速度误差Fig.7 Horizontal relative velocity estimation error between target and detector

表1给出了3 种跟踪算法经过100 次蒙特卡罗仿真后得到的相对距离，相对速度的均方根误差RMSE 和运算时间。其中表示目标与探测器之间距离的均方根误差分别为目标与探测器之间在水平和垂直距离上的均方根误差，t 表示运行100 次蒙特卡罗仿真的时间，t'表示在一次完整的仿真中，每完成一次状态向量更新所使用的时间。

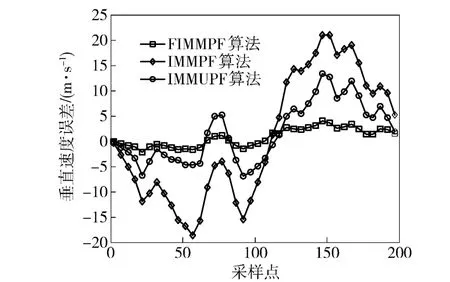
图8 目标与探测器垂直相对速度误差Fig.8 Veritcal relative velocity estimation error between target and detector

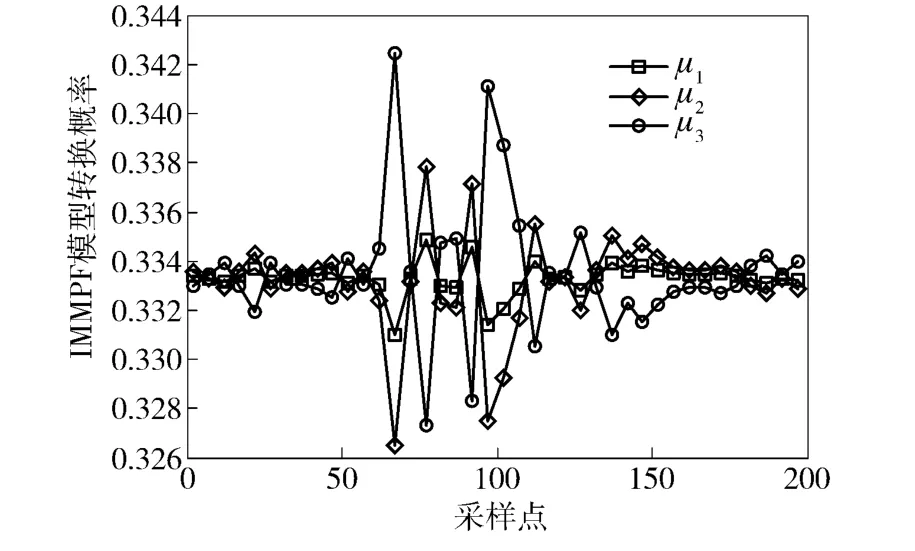
图9 IMMPF 中3 种模型概率变化曲线Fig.9 The probability curves of three models of IMMPF

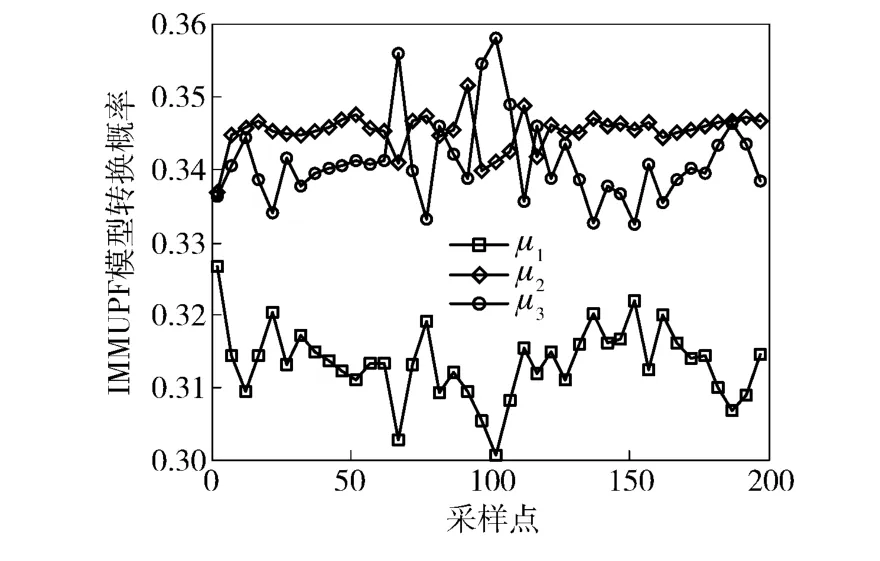
图10 IMMUPF 中3 种模型概率变化曲线Fig.10 The probability curves of three models of IMMUPF

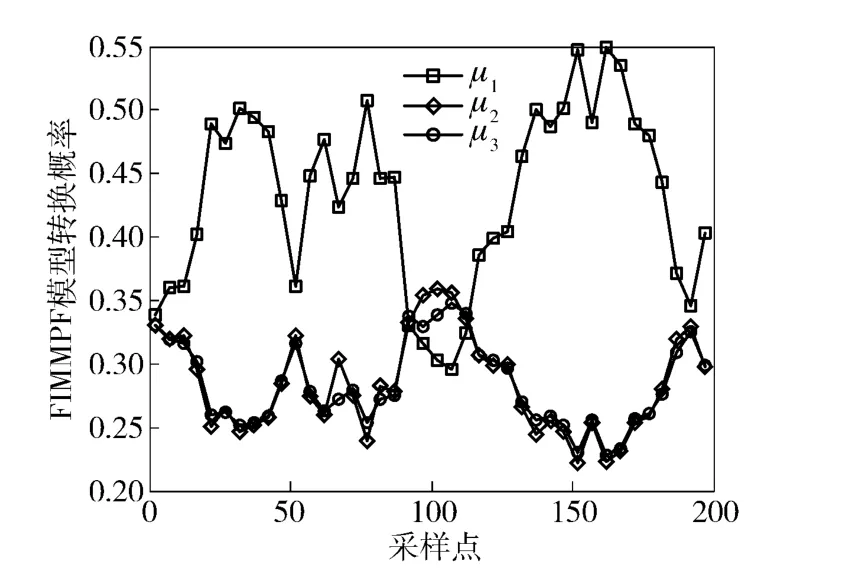
图11 FIMMPF 中3 种模型概率变化曲线Fig.11 The probability curves of three models of FIMMPF

从3 种目标跟踪算法得到的相对距离误差曲线图、相对速度误差曲线图、3 种模型概率变化曲线图和表1中的数据可以看出，由于模糊控制方法在每一次状态更新时，实时调整模型转换概率矩阵，使与目标当前运动状态最接近的运动模型在混合产生这一采样时刻的初始状态向量里占有更大的比重，因此，FIMMPF 的目标跟踪精度最高，其次是IMMUPF，而IMMPF 的精度最低。从计算时间上，IMMUPF 在完成每一次目标状态向量更新的时间是最长的，其次是IMMPF，而FIMMPF 所需的时间最短。这是因为中心差分扩展卡尔曼滤波算法只在计算残差协方差矩阵时用中心差分公式完成非线性观测方程传递函数偏导数的计算，而其他部分与扩展卡尔曼滤波算法相同，因此，中心差分扩展卡尔曼滤波算法的运算时间很短。

4 结论

研究了基于旋转式三维静电探测器的机动目标跟踪问题，建立了探测低空飞行目标的数学模型。针对测量方程为非线性的特点和机动目标跟踪问题，为了提高滤波算法的精度，减少计算时间，提出了一种新的适用于静电机动目标跟踪的FIMMPF.理论分析与仿真结果表明，FIMMPF 比IMMUPF 和IMMPF 更适用于机动运动的静电目标跟踪。

References)

［1］郝晓辉，虞健飞，崔占忠. 直升机静电场研究［J］. 兵工学报，2012，33(5):583 -587 HAO Xiao-hui，YU Jian-fei，CUI Zhan-zhong. Research on electrostatic field of helicopter［J］. Acta Armamentarii，2012，33(5):583 -587. (in Chinese)

［2］毕军建. 对空弹药引信用静电矢量探测技术研究［D］. 北京:北京理工大学，2003.BI Jun-jian. Electrostatic vector probing technology research of air ammunition fuze［D］. Beijing:Beijing Institute of Technology，2003. (in Chinese)

［3］代方震. 基于电极扫描原理的被动式静电探测技术研究［D］.北京:北京理工大学，2004.DAI Fang-zhen. Based on the principle of passive electrode scanning electrostatic detection technology research［D］. Beijing:Beijing Institute of Technology，2004. (in Chinese)

［4］陈曦.被动式地面静电探测技术研究［D］. 北京:北京理工大学，2005.CHEN Xi. Research on the ground passive electrostatic detection technology［D］. Beijing:Beijing Institute of Technology，2005.(in Chinese)

［5］付巍.低空目标静电探测与跟踪算法［D］. 北京:北京理工大学，2009.FU Wei. The low altitude target detection and tracking based on electrostatic detectors［D］. Beijing:Beijing Institute of Technology，2009. (in Chinese)

［6］Boers Y，Driessen J N. Interacting multiple model particle filter［J］. IEEE Proceedings of Radar Sonar and Navigation，2003，150(5):334 -349.

［7］Sanjeev M，Simon M. A tutorial on particle filter for online nonlinear/non-Gaussian Bayesian tracking［J］. IEEE Trans on Signal Processing，2002，50(2):174 -188.

［8］Hu Z T，Pan Q. An improved Particle filtering algorithm based on observation inversion optimal sampling［J］. Journal of Central South University of Technology，2009，16(5):815 -820.

［9］刘尚合，武占成. 静电放电及危害防护［M］. 北京:北京邮电大学出版社，2004:35 -36.LIU Shang-he，WU Zhan-cheng. Electrostatic and discharge and damage protection［M］. Beijing:Beijing University of Posts and Telecommunications Press，2004:35 -36. (in Chinese)

［10］曹阳，赵明富，罗彬彬，等. 机载空间光通信平台的交互多模型粒子滤波跟踪算法［J］. 红外与激光工程，2012，41(11):3065 -3068.CAO Yang，ZHAO Ming-fu，LUO Bin-bin，et al. Airbone platform＇s tracking algorithm for free space optical communication based on IMMPF methods［J］. Infrared and Laser Engineering，2012，41(11):3065 -3068. (in Chinese)

［11］Zahir M，Abdelaziz O. Comparision of interactive multiple model partide filter and interactive multiple model unscented particle filter for tracking multiple manoeuviring targets in sensors array［J］. IEEE Proceedings of Cybernetic Intelligent Systems，2010，41(1):1 -6.