输出控制的混沌同步保密通信系统设计和应用

孙楚旻

（北京师范大学物理学系 北京 100875）

0 引言

随着现代化经济的快速发展，我国的计算机和各种通信网络的技术也逐渐的趋向成熟，现阶段，计算机通信、网络以及微电子学等有关学科也更加注重对保密通信上的研究，同时混沌运动又是一种确定性的非线性运行，虽然混沌运动有着非常复杂的运动轨迹，但是在某种程度上而言，其又有着非周期和连续宽带频谱的特点，被广泛的应用于保密通信领域。在现代化工程技术中最常用的一种方法则是混沌系统的线性化了，一般情况下，传统的线性化基本上都是在在系统的相对平衡点的附近尽可能的取线性近似，以便于得到线性化的系统，但是就某一角度而言，这种简单传统的线性化系统紧紧适用于平衡点附近的线性化。在现代化这个大系统大工作大工作范围下的工程技术，则就要在一定能够程度上打破线性近似的局限，进而寻找以一种有效的方法进行精确线性化的测量，在一定程度上完成相应的保密通信。

1 混沌运动的特点

混沌运动作为一种确定性的随机现象，比较贴切与科学和工程学中的非线性系统理论，同时混沌现象对客观世界通用的数学物理方法和概念有着一定的影响作用。在混沌现象发生之前，其客观现象的解释仅仅局限于确定伦和概率论上，往往有着其不确定性的因素，但是就现在而言，混沌现象往往有着一定的确定性，但是这种一定的确定性往往还存在着一些内在的随机性。一般情况下混沌在一定程度上并没有严格的定义，更多的是大概的概念，下面介绍几个相对来说有代表性的定义。

定义 1.1[4]考虑一维映射 F :J →J,J⊆R是一个区间。A ⊂J成为 F的一个混沌，如果：

A是一个不变集，即 AAF ⊆)( ； F在 A中的所有周期点几何在 A中稠，即对 ∀ ε＞0,∀x∈A,(x−ε,x+ε)区间中总有F的周期点；存在 F在 A中的一个非周期轨线在 A中稠。

定义 1.3[5]（Devaney的混沌定义）：设V 为一度量空间，称映射 VVF →: 在V上使混沌的，但是若 f满足下面三个条件：

初值敏感性。即对 Vx∈∀＞∀ 和0ε，在x的区间范围内存在V和自然数n，使得： d ( fn(x),fn(y))＞δ。拓扑传递性。对 V上的任意开集 X,Y，存在 K ＞0, st.fk(x)∩Y ≠φ。周期点的稠密性。 f的周期点集在v中稠密。

通过对其定义做一个详细的分析比较，我们发现，拓扑传递性在一定程度上则是对任意一个点的领域在 f作用下都会对整个度量的空间v进行一定的覆盖。并且混沌系统和随机系统本质的一个区别则是周期点的稠密性，但是就某一种意义来说，虽然混沌现象在一定形式上是一种伪随机现象，但是，混沌系统不仅仅有着很强的确定性，同时也有着一定的规律性。总之混沌运动在一定程度上主要有有界性、遍历性、内随机性、分维性、标度性、普适性以及统计性等特点。

2 混沌系统的同步

一般情况下，混沌系统的同步主要是从两个不同的初始点出发的两个混沌系统，在经过时间的一定推移，这两个混沌系统的运动轨线就会尽可能的融为一体，但是就某种程度来说这种同步并不只是随机变化的，而是相对的稳定。

其混沌同步的类型主要有完全同步、相同步、广义同步、投影同步以及延迟同步这五种。但是就混沌同步的方法而言，又可以分为驱动-响应同步法、主动-被动同步法、反馈同步法以及基于观测器的同步法四种方法。就其反馈同步法而言，这种方法在实际的应用中与混沌控制有着一定程度上的关联，但是一般情况下，混沌同步常常用参数反馈和状态变量反馈两种方法进行一定程度上的反馈。

3 同步混沌保密通信的主要技术

目前保密通信系统的设计通常会使用同步的混沌，就其根本上而言，混沌同步在保密通信中的应用主要表现在三个技术上的应用，分别是混沌遮掩、混沌调制以及混沌开关技术。

然而其混沌调制在一定程度上又可以叫做款普发射。往往这种混沌调制在实际的混沌保密通信中是特别复杂的。但是随着我国现代化经济快速的发展，我国的混沌调制技术也逐渐趋于更加的完善。

4 基于输出控制的混沌同步的保密通信

一般情况下，这种输出控制下的混沌同步保密通信，其非线性系统往往如下所示

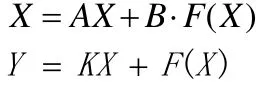
其中的A∈Rn×n, B∈Rn×m, F∶Rn→Rm( m ≤n),F(X)为非线性映射，AX为线性部分， )(XFB⋅ 为非线性部分，Y为系统的输出，K为待定常数。

然而，就混沌同步保密通信系统的原理而言，其主要的原理图如图1所示

图1 混沌发送系统

该系统在是实现保密通信的时候主要通过先对信息信号进行一定的加密，之后使得发射机和接收机同步，最后才进行信息信号解密。

首先就其信息信号加密而言，s是作为一种将要发送的一种信号，这就在一定程度上使得加密的函数表达式是Φ(X,s)=f1(X)+f2(X)s。

其次就发射机和接收机的同步而言，我们知道，在信息信号进行一定程度上的加密之后，则就要在一定程度上继续拧混沌调制和混沌掩盖，进而也就得到这样的非线性发送系统：

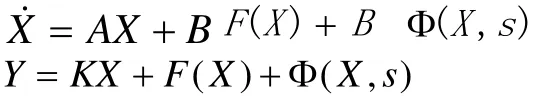
其中，在这样的一个非线性的发送系统下，在一定程度上也就形成了一种非线性的映射，同时混沌调制在根本上对混沌系统的混沌特性并没有太大的影响，这就在一定程度上说明该非线性系统在某一角度上仍然是一种混沌系统，有着其稳固的状态，并在一定程度上使得系统的收发端做到真正意义上的同步。

最后就其信息信号解密而言，在一定程度上为了更好的使得信息信号能够很好的被接受，则就要对信息信号进行恢复，通过一定的加密之后再对信息信号进行一定原则上的解密，总之，在最后得到的解密信息信号则是：

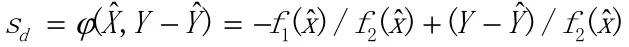
5 复杂网络中各个节点之间的保密通信

我们都知道网络的出现在很大程度上改变了大多数人的生活习惯，但是，在人们对网络越来越依赖的同时，也更加注重其网络的安全性，这就在一定程度上强调了信息要有一定的保密性。但是混沌同步下的保密通信其复杂网络之间有着各种各样的复杂性。

无论是网络同步还是混沌同步，都有着其重要的保密通信方案，在现如今复杂的网络各个节点之间，信息的传输是时时刻刻都在进行着，并且在一定程度上，其传输的信息优势相对的安全，处于一种秘密的状态，但是这种保密式的信息传输，则是运用发送端的混沌系统的输出，在一定程度上对所要传送的信号进行一定原则上的遮掩，这样被传输的信号不仅仅是传输的初始信号和混沌发送端输出的一种信号，同时也是对被传输的信号和发射端系统所输出的信号的一个传输过程，最后在接收端通过混沌同步进而恢复刚开始所传输的信号。

6 结语

输出控制的混沌同步保密通信系统的应用，在一定程度上满足了现代人类对网络的安全保密的一个需求。通过本文对一些非线性反馈控制几何理论的研究分析以及对混沌运动的综合概述，我相信输出控制的混沌同步在未来的保密通信系统的应用将会有着更广阔的应用前景，能够更好的满足现代化人们对网络平台上信息安全性、保密性的需求。

[1]黄丽莲，尹启天.基于输出控制的混沌同步保密通信系统[J].电子与信息学报，2009，31（10）：2402-2405.

[2]尹启天.混沌系统的同步及其在保密通信中的应用[D].哈尔滨工程大学，2008.

[3]黄丽莲.混沌系统的同步控制问题研究[D].哈尔滨工业大学，2005.

[4]王瑞兵.复杂网络的同步及其在保密通信中的应用[D].江苏大学，2007.

[5]郭丽.复杂网络之间的混沌同步研究[D].辽宁师范大学，2011.

[6]王瑞兵，姚洪兴.复杂网络的同步及保密通信[J].微计算机信息，2007，23（30）：103-104，199.