楔环连接结构对鱼雷壳体声辐射的影响分析

马锐磊, 尹韶平, 曹小娟, 严 海, 秦晓辉



楔环连接结构对鱼雷壳体声辐射的影响分析

马锐磊1,2, 尹韶平1,2, 曹小娟1, 严 海1, 秦晓辉1

(1. 中国船舶重工集团公司 第705研究所, 陕西 西安, 710075; 2. 水下信息与控制重点实验室, 陕西 西安, 710075)

针对鱼雷楔环连接结构对壳体声辐射的影响问题, 综合运用有限元法和边界元法对其进行了分析, 首先建立了鱼雷有限元模型, 并对模型进行了模态仿真计算, 通过试验对模型的准确性进行了验证; 通过声学软件LMS Virtual. Lab Acoustics中的边界元法对模型进行了辐射声功率计算, 比较了有楔环模型与无楔环模型的声功率曲线, 并给出典型频率的声压级云图。仿真结果表明, 有楔环状态下的总辐射声功率比无楔环状态下低10 dB左右, 可为后续鱼雷噪声预报及噪声控制提供参考。

鱼雷壳体; 楔环连接结构; 模态; 辐射声功率; 声压级云图

0 引言

鱼雷是一种涉及机械、电子、力学、动力、控制、水声、爆炸等多学科的高技术水下精确制导武器。鱼雷产品为了满足生产、加工、调试、安装、维修使用和保障等方面的需求, 必须进行必要的分段。进行鱼雷舱段间的连接设计时, 必须在满足强度、刚度和密封要求的前提下, 做到拆装使用方便, 并尽量保证雷体表面的光顺, 提高保障性。鱼雷舱段连接方式最常用的是楔环连接。楔环连接结构具有雷体表面光顺、占用壳体内部空间小、结构尺寸紧凑, 质量轻、连接可靠、壳体受力均匀等优点[1]。

随着声纳系统、电子技术和信号处理技术的快速发展, 声纳系统对水下目标的识别和跟踪能力大大提高, 从而对鱼雷的声隐身技术提出了更高的要求。只有尽量降低鱼雷的水下声辐射, 才有可能提高其隐蔽性和导引距离。鱼雷壳体是金属薄壳结构, 在激励作用下振动的随机响应所产生的二次声辐射是鱼雷水下主要噪声源之一, 因此, 对壳体的声辐射研究十分必要。文献[2]联合有限元法和边界元法对流场中的圆柱壳点声源激励下的声辐射作了数值计算, 预报了圆柱壳的内外场声压, 得到了圆柱壳的声辐射功率曲线。文献[3]研究了两端简支单层圆柱壳振动模态与声辐射模态的耦合关系, 计算了结构的辐射声功率。文献[4]在文献[5]和[6]研究的基础上, 具体比较了机械力与声源2种激励作用下环肋圆柱壳的水下声辐射特性以及传递损失。但是, 以上研究中均采用有限长单段圆柱壳体, 未考虑连接关系影响。针对鱼雷自身连接结构特点, 本文采用楔环连接状态下的2段圆柱壳体, 运用有限元法和边界元法对其建立了有限元模型和边界元模型, 并通过模态试验对模型进行了验证, 最后通过LMS. Virtual. Lab Acoustics软件得到了其辐射声功率和声压级云图, 并与无楔环状态结果进行了对比。

1 基本理论

1.1 模态理论

结构系统的动力学方程通常可表示为

略去结构系统运动方程中的阻尼力项和外载荷项, 得到系统无阻尼自由振动的动力学方程

令式(2)的解为

(3)

代入式(2)可得

(5)

1.2 耦合边界元理论

耦合直接边界元网格可分为2个部分, 一部分是与结构网格耦合的部分, 包含1个节点, 另一部分是不参与耦合的部分, 包含2个节点(1+2=), 这样直接边界元上的声压和速度可以写为

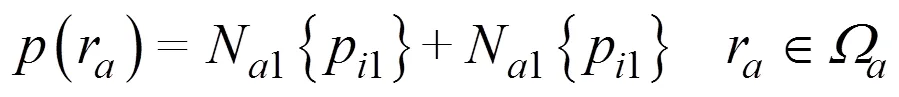
由于声压作用在结构上, 作为1个载荷, 同样可以引起结构振动, 这部分结构的动力学方程为

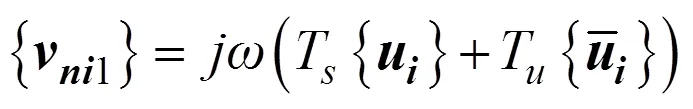
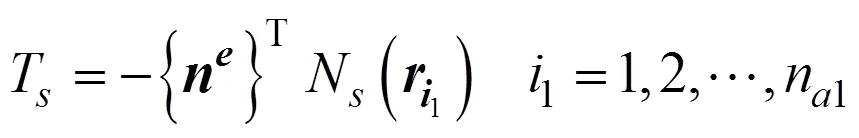
对于边界元上任意节点, 有

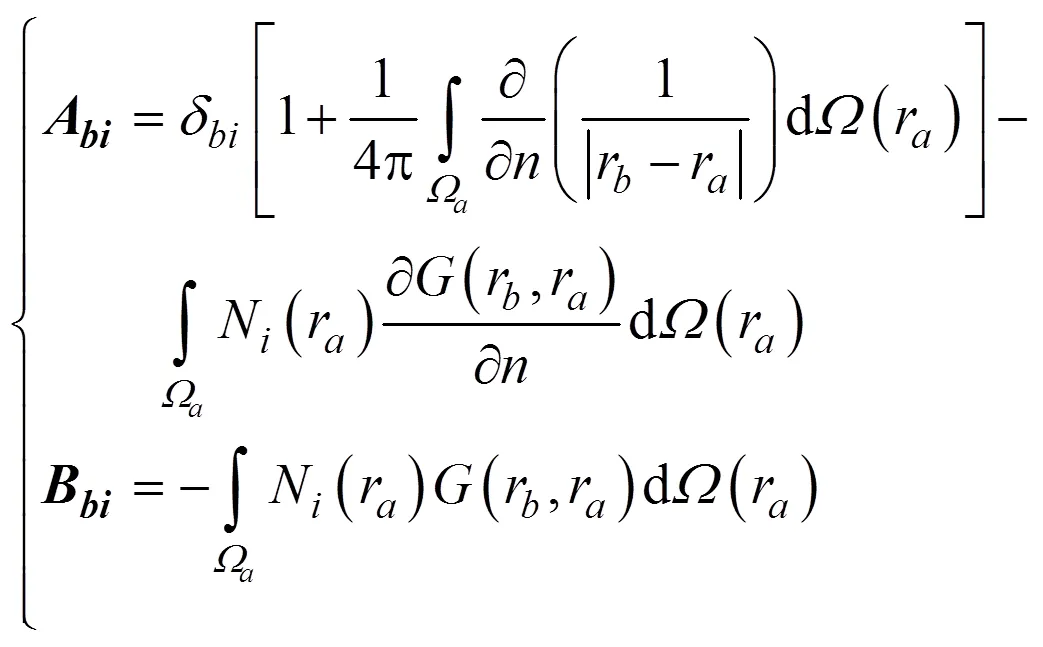
将式(10)代入式(13), 可得

结合结构有限元方程式(8)和直接边界元式(14), 可以得到耦合边界元方程为

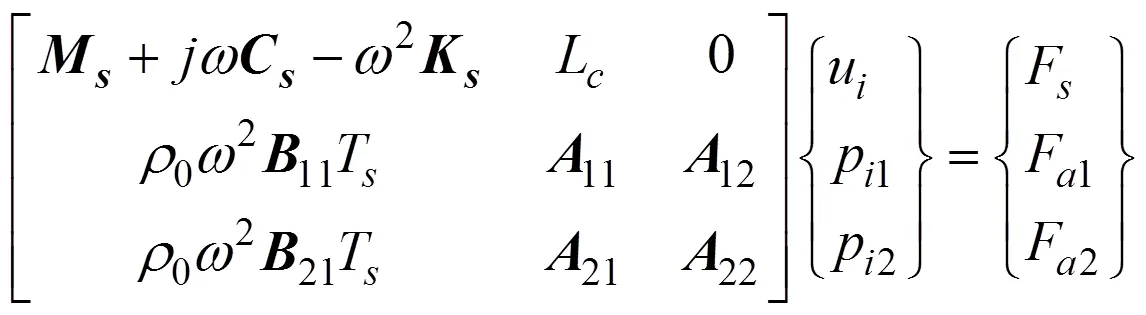
式中

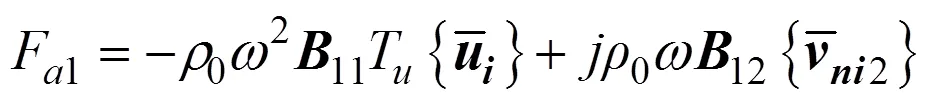
在特殊情况下, 直接边界元的整个网格都与结构网格耦合, 这时的耦合方程变为

式中

2 模型建立与验证

为比较分析, 本文选取采用楔环结构连接的2段壳体以及不带有楔环连接的光滑壳体分别进行建模, 2种几何模型全长440 mm, 外径324 mm, 壳体厚度5.5 mm。将几何模型以*×stp文件格式导入有限元前处理软件HyperMesh中, 忽略模型中倒角等微小特征, 采用hex8六面体单元、penta6五面体单元以及tetra4四面体单元对模型进行网格划分, 其中楔环连接结构模型根据参考文献[7]和[8]的方法建立, 鱼雷壳体有限元模型见图1。

图1 鱼雷壳体有限元模型

为验证带有楔环连接结构模型的准确性, 对其进行了模态试验, 通过有限元仿真计算与试验结果的对比, 说明模型的有效性。本文采用MSC. Nastran计算了模型的前10阶模态, 计算参数: 材料弹性模量取69 GPa; 泊松比取0.33; 材料密度取2.7×10–9t/mm3, 由于篇幅所限, 故选取几个典型结果。有限元计算与试验固有频率对比结果如表1所示, 模态振型对比结果如图2所示。

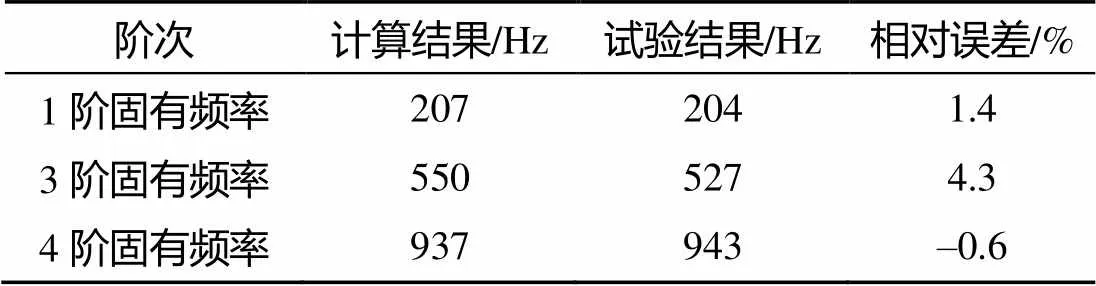
表1 仿真计算与试验结果对比

通过表1可以看出, 仿真计算和试验得到的固有频率结果相对误差最大不大于5%, 满足工程计算精度要求。

从振型对比结果可以看出: 1) 二者的第1阶模态振型均为两端面产生椭圆形变形, 且两端变形方向相互垂直; 2) 二者的第3阶模态振型均为两端面产生三角形变形, 且两端变形方向相互垂直; 3) 二者的第4阶模态振型均为两端面产生四角形变形, 且两端变形方向相互垂直; 通过固有频率值与模态振型的对比, 可以说明有限元模型的准确性, 从而为后续声学仿真计算提供支撑。

图2 模态振型计算与试验结果对比图

3 仿真结果与分析

本文采用边界元法进行声学计算, 计算时需要对模型建立边界元网格, 即声学网格, 边界元网格划分具有一定要求: 每个波长内至少要包含6个单元[9-10], 即要满足

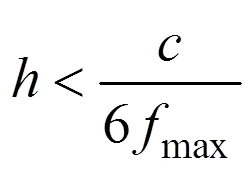
式中:为单元边长;max为所计算的最高频率。

对于水介质, 声速=1 500 m/s, 分析的最高频率max=2 kHz, 则根据式(21), 声学网格单元边长应不大于125 mm。利用HyperMesh软件建立的模型边界元网格如图3所示, 网格尺寸不大于50 mm。

图3 边界元模型

将圆柱壳体的有限元模型(*.bdf文件)、模态仿真计算结果(*.op2文件)以及边界元网格模型(*.bdf文件)导入LMS Virtual.Lab Acoustics软件中, 建立创建声场网格及场点网格, 定义声场介质及边界条件; 在圆柱壳体内部加载单位力激励, 设置声辐射计算频率范围为1~2 000 Hz, 步长为1 Hz, 利用边界元法对其进行声学仿真。2种模型2 kHz内壳体的辐射声功率随频率变化对比曲线如图4所示。

图4 辐射声功率对比曲线

从仿真结果可以看出, 有楔环状态下的总辐射声功率比无楔环状态下低10 dB; 有楔环状态下辐射声功率最高的频率点较无楔环状态左移, 说明楔环连接结构使模型整体刚度有所下降; 总体上, 在辐射声功率最大的几个频率点, 有楔环状态较无楔环状态辐射声功率值小。

取模型中间部位径向截面, 分别比较有楔环模型辐射声功率最大的2个频率点569 Hz和1 083 Hz及无楔环模型最大的2个频率点158 Hz和1 031 Hz时的声压云图, 如图5所示。图中, 左图均为有楔环状态, 右图均为无楔环状态。

从对比结果看出, 在158 Hz时2种模型的声压云图比较相似; 在569 Hz, 1 031 Hz和1 083 Hz时, 无楔环模型的云图形状较有楔环模型更均匀、规则。

4 结论

本文结合有限元以及边界元方法对鱼雷有、无楔环连接的壳体结构辐射声功率进行了对比分析, 得到了以下结论。

1) 有楔环状态下的总辐射声功率比无楔环状态下低10 dB; 在辐射声功率最大的几个频率点, 有楔环状态较无楔环状态辐射声功率值小。

图5 2种模型在典型频率点声压云图对比

2) 楔环连接结构使模型整体刚度有所下降, 使模型固有频率值降低;

3) 从声压云图上看, 除在158 Hz时2种模型的声压分布云图比较相似外; 在569 Hz、1 031 Hz和1 083 Hz时, 无楔环模型的声压云图较有楔环模型更加均匀、规则。

本文通过对鱼雷楔环连接结构对壳体声辐射的影响研究, 为后续鱼雷噪声预报及噪声控制提供参考。

[1] 尹韶平, 刘瑞生. 鱼雷总体技术[M]. 北京: 国防工业出版社, 2011.

[2] 陈美霞, 邱昌林, 骆东平. 基于FEM/BEM法的内部声激励水下圆柱壳声辐射计算[J]. 中国舰船研究, 2007, 2(6): 50-54. Chen Mei-xia, Qiu Chang-lin, Luo Dong-ping. Sound Radiation Analysis of Submerged Cylindrical Shell Ex- cited by Interior Point Source Based on FEM/BEM[J]. Chinese Journal of Ship Research, 2007, 2(6): 50-54.

[3] 和卫平, 陈美霞, 魏建辉, 等. 基于有限测点的单层圆柱壳辐射声功率计算[J]. 船舶力学, 2012, 16(10): 1204-1211.He Wei-ping, Chen Mei-xia, Wei Jian-hui, et al. Calcu- lation of Acoustic Power Radiated from a Cylindrical Shell Based on a Limited Number of Measurements[J]. Journal of Ship Mechanics, 2012, 16(10): 1204-1211.

[4] 彭旭, 关珊珊, 骆东平, 等. 内部声激励下加筋圆柱壳的声辐射特性分析[J]. 固体力学学报, 2007, 28(4): 355-361.

[5] 陈美霞, 骆东平, 陈小宁, 等. 复杂双壳体声辐射性能分析[J]. 声学学报, 2004, 29(3): 209-215. Chen Mei-xia, Luo Dong-ping, Chen Xiao-ning, et al. Analysis of Sound Radiation Characteristics of Complex Double Shells[J]. Acta Acustica, 2004, 29(3): 209-215.

[6] 骆东平, 张玉红. 环肋增强柱壳振动特性分析[J]. 中国造船, 1989(1): 64-74.

[7] 刘晓欧, 尹韶平, 严光洪. 基于MSC Nastran的水下环肋圆柱壳体振动模态计算方法[J]. 计算机辅助工程, 2006, 15(增刊): 124-127. Liu Xiao-ou, Yin Shao-ping, Gao shan. Underwater Vibra- tion Modal Calculation of the Ring-stiffened Cylindrical Shell with MSC Nastran[J]. Computer Aided Engineering, 2006, 15(S1): 124-127.

[8] 严光洪, 张志民. 接触壳体的模态计算[C]//MSC. Software中国用户论文集, 2004.

[9] 杜功焕, 朱哲民, 龚秀芬. 声学基础[M]. 第三版. 南京: 南京大学出版社, 2012.

[10] 李增刚, 詹福良. Virtual.Lab Acoustics声学仿真计算高级应用实例[M]. 北京: 国防工业出版社, 2010.

(责任编辑: 陈 曦)

Effect of Wedged Ring Connection Structure on Noise Radiation of Torpedo Shell

MA Rui-lei,YIN Shao-ping, CAO Xiao-juan,YAN Hai, QIN Xiao-hui

(1. The 705 Research Institute, China Shipbuilding Industry Corporation, Xi¢an 710075, China; 2. Science and Technology on Underwater Information and Control Laboratory, Xi¢an 710075, China)

Both finite element method and boundary element method are adopted to analyze the effect of the wedged ring connection structure on the noise radiation of torpedo shell. First, the finite element models for a torpedo are established, and then the accuracy of the models are verified through modal testing. Second, the models′ radiated sound power is calculated by using the boundary element method in the software LMS Virtual. Lab Acoustics. The curves of sound power for both models with and without wedged ring connection structure are compared, and the sound pressure level contours for typical frequency are obtained. The results indicate that the total sound power of the model with wedged ring structure is 10 dB lower than that of the one without wedged ring structure. This study may facilitate noise prediction and noise control of a torpedo.

torpedo shell; wedged ring connection structure; modal; radiated sound power; sound pressure level contour

TJ630.31

A

1673-1948(2014)03-0169-05

2014-02-25;

2014-03-19.

马锐磊(1987-), 男, 在读硕士, 研究方向为武器系统总体技术.