主动自导回波信号的非线性动力学特性

申 珅, 程 宏, 王明洲



主动自导回波信号的非线性动力学特性

申 珅1,3, 程 宏2, 王明洲1, 3

(1. 中国船舶重工集团公司 第 705 研究所, 陕西 西安, 710075; 2. 昆明船舶设备研究试验中心, 云南 昆明, 650051; 3. 水下信息与控制重点实验室, 陕西 西安, 710075)

以非线性动力学的基本理论和目标回波信号的非线性化为理论基础, 分别讨论了正弦信号、主动自导回波信号以及经过滤波处理后的主动自导回波信号的相轨迹运动特性。对一定数量的实测主动自导回波信号数据进行了仿真处理, 仿真结果表明, 经滤波处理后的主动自导回波信号具有非线性特性, 且其相轨迹运动特性及点距和特征参数均成一定的规律性, 具有可分性。

主动自导回波信号; 目标回波信号; 相轨迹; 点距和

0 引言

主动自导回波信号是一种波形或其参量不确定的随机信号, 是通过目标对主动自导信号的调制而得来的, 它蕴藏着目标的全部信息。对于主动自导回波信号的分析和处理, 过去人们一直以传统的信号处理理论为基础, 即以平稳性、随机性来刻画主动自导回波信号。随着非线性动力学理论的发展, 人们发现一些常被认为是随机的现象具有混沌特性, 主动自导回波信号便是其中之一[1-3]。本文以非线性动力学理论为基础, 研究了主动自导回波信号的相轨迹运动特性及点距和特性。分别计算了正弦信号、实测的主动自导回波信号和滤除混响、噪声后的主动自导回波信号的相轨迹和点距和。通过对计算结果的分析, 验证了主动自导回波信号具有非线性特性。

1 非线性动力学理论

1.1 动力学理论的基本概念

动力学理论是研究运动随时间变化的理论, 它主要试图通过抽象出运动的特性并建立起数学模型, 来解决已知过去和现在条件下如何预测未来的问题。这些用来描述运动的某种特性随时间变化的数学模型或准则, 就称为动力系统。而用于描述动力系统所使用的信息, 概括起来称为状态。当动力系统在时间上连续变化时, 则可以表示为微分方程组的形式, 即

1.2 目标回波信号的非线性化

目标回波信号是发射信号和目标相互作用产生的, 即目标回波信号是目标对发射信号的调制结果。目标回波信号相对于发射信号, 存在着多普勒频移、距离延伸或持续时间的扩展、调制效应和频域上的共振峰等现象。目标回波信号可表示为

对式(2)两边分别求导, 可得

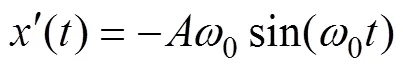
将式(3)写成式(1)的形式, 得

式(4)表示一个非线性动力学系统。本文以上述非线性动力学理论为基础, 主要研究该系统的状态量随着时间的变化在相平面内所形成轨迹的变化趋势。

2 正弦信号的相轨迹特性

正弦信号是频率成分最为单一的一种信号。任何复杂信号都可以通过傅里叶变换分解为许多频率不同、幅度不等的正弦信号的迭加。正弦信号可表示为

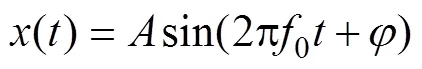
本文主要研究正弦信号的非线性特性, 令

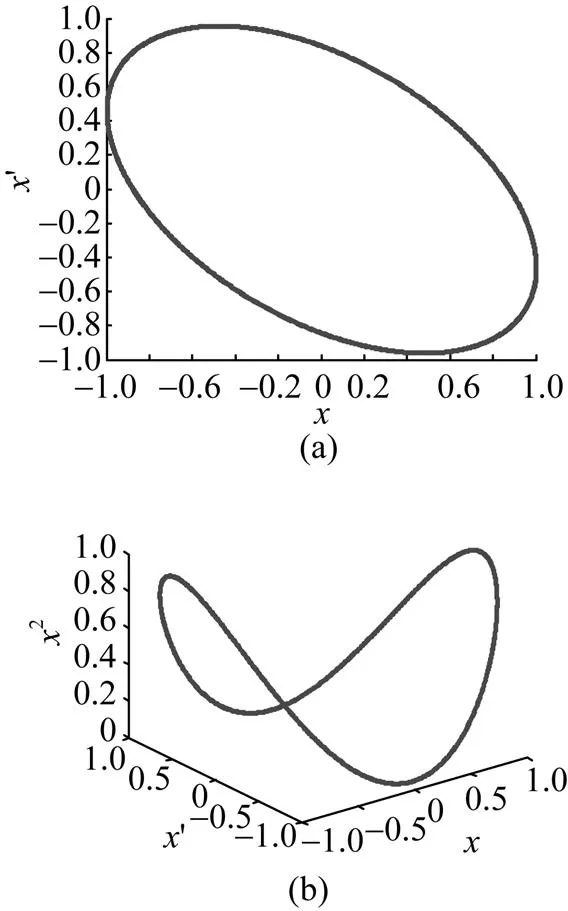
图1 正弦信号的相轨迹图

3 主动自导回波信号的相轨迹特性

选择试验中自导系统接收到的主动自导回波信号作为样本数据, 该主动自导回波信号中包括混响、环境噪声及目标回波信号等。已知自导系统的发射信号是矩形波, 信号脉宽为24 ms, 数据为复数形式,共有10个周期的主动自导回波信号数据样本。

3.1 原始数据样本分析

1) 选取4个周期的实测数据样本。对各周期数据进行滑动窗快速傅里叶变换(fast Fourier transform, FFT), 确定目标回波信号及其位置。根据自导发射信号的脉宽, 可确定FFT变换滑动窗长度为480, 将各周期数据按480个点为一个组, 每次滑动1/4个窗长度算为下一个组, 从而将整个周期数据样本分成若干个小组, 分析结果如表1所示。

表1 各周期中目标回波信号段

2) 将各周期数据分组后, 分别从各周期中随机选取3组不含目标回波信号的原始数据和3组包含目标回波信号的原始数据, 观察各组数据的相轨迹运动规律。图2是第1周期的6组数据样本相轨迹图。

3.2 滤波后数据样本分析

对实测的原始数据样本进行滤波处理, 只保留目标回波信号, 然后对各周期信号做上述同样的分析, 观察其相轨迹运动的变化。图3是第1周期实测信号经滤波处理后的6组数据相轨迹图。

由图3可看出, 包含目标回波信号段(72组、73组、74组)与不包含目标回波信号段(22组、41组、61组)的其相轨迹完全不同。包含目标回波信号段的其相轨迹类似于正弦信号的相轨迹, 呈椭圆形绕动。而不包含目标回波信号段的其相轨迹随机聚集在坐标中心位置, 无规律可寻。由此可知, 其相轨迹的运动特性具有显著的可分性。

3.3 点距和分析

图2 第1周期信号样本相轨迹图

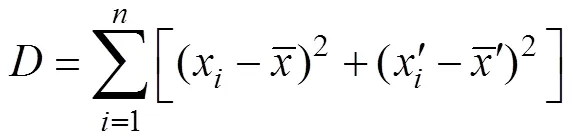
表2是第一周期信号原始数据样本的分析结果, 由表可知, 包含目标回波信号的3组和不包含目标回波信号的3组其中心点、点距和都没有什么规律可循, 不具有可分性。

表3是对第1周期信号进行滤波处理后的分析结果, 由表可看出, 包含目标回波信号的3组与不包含目标回波信号的3组其中心点也没有什么规律可循, 但其点距和有着明显的差异, 含目标回波信号的3组其点距和远远大于不含目标回波信号的3组, 其点距和相差一个数量级。因此可知其点距和特性具有一定得可分性。

图3 滤波后第1周期信号相轨迹图

表2 第1周期原始信号特性

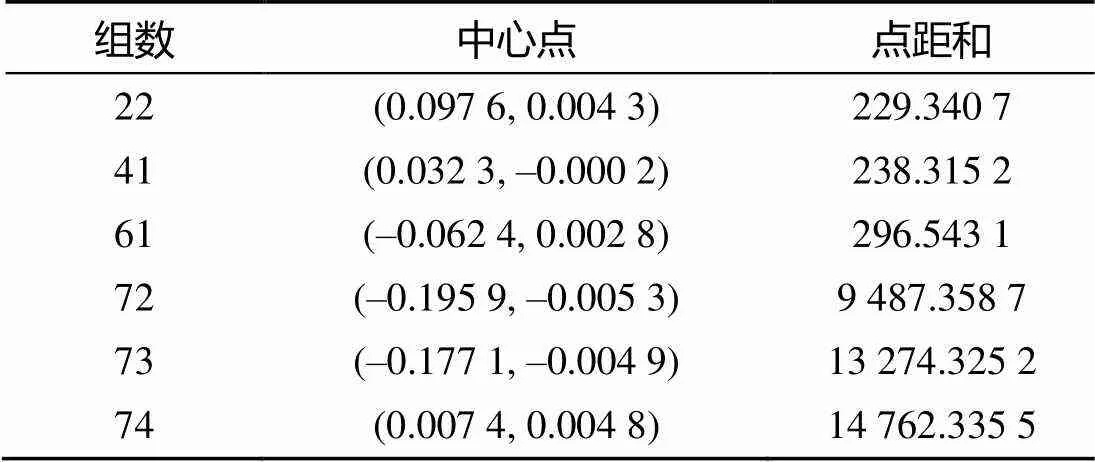
表3 滤波后第1周期信号特性

4 结束语

本文研究了正弦信号和主动自导回波信号的非线性动力学特性。针对一定样本数目的实测主动自导回波信号, 分别计算原始数据和经滤波处理后数据的相轨迹、中心点及点距和。结果表明, 经滤波处理后的主动自导回波信号的相轨迹运动特性类似于正弦信号的相轨迹运动特性, 并且其点距和具有一定的可分性。这一结果对于水下目标回波信号的特征识别具有一定的参考价值。

[1] 郭丽华, 王大成, 丁士圻. 水下目标提取方法研究[J]. 声学技术, 2005, 24(3): 148-151.Guo Li-hua, Wang Da-cheng, Ding Shi-qi. Extraction of Features of Underwater Target[J]. Technical Acoustics, 2005, 24(3): 148-151.

[2] 李亚安, 徐德民. 基于Lyapunov指数的水下目标信号混沌特征提取[J].西北工业大学学报, 2002, 20(4): 633- 636.

[3] Frison T W. Abarbanel H D I. Chaos in Ocean Ambient Noise[J]. Journal of Acoustical Society of America, 1996, 99(3): 1527-1539.

[4] 黄永念. 非线性动力学引论[M]. 北京: 北京大学出版社, 2010.

[5] Kaplan D, Glass L. Understanding Nonlinear Dynamics[M]. Berlin: Springer Verlag, 1997.

[6] 聂春燕. 混沌系统与弱信号检测[M]. 北京: 清华大学出版社, 2009.

[7] 李志舜. 鱼雷自导信号与信息处理[M]. 西安: 西北工业大学出版社, 2004.

(责任编辑: 杨力军)

Nonlinear Dynamic Characteristics of Active Homing Echo Signal

SHEN Shen,CHENG Hong,WANG Ming-zhou

(1. The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710075, China; 2. Kunming Shipborne Equipment Research & Test Center, Kunming 650051, China; 3. Science and Technology on Underwater Information and Control Laboratory, Xi′an 710075, China)

We discuss the phase trajectory motion characteristic of the sinusoidal signal, the active homing echo signal, and the filtered active homing echo signal based on the theories of nonlinear dynamics and nonlinearization of target echo signal. And we conduct a simulation with a certain number of measured active homing echo signal data. Simulation results indicate that the filtered active homing echo signal shows nonlinear characteristics, and its phase trajectory motion characteristic and point distance sum-based parameter exhibit certain regularity and separability.

active homing echo signal; target echo signal; phase trajectory; point distance sum-based

TJ630.1; TB561

A

1673-1948(2014)01-0026-04

2013-09-02;

2013-11-18.

申 珅(1989-), 女, 在读硕士, 研究方向为水声工程.