粗糙海底单基地散射和混响建模与仿真

王 松, 梁 红, 杨长生



粗糙海底单基地散射和混响建模与仿真

王 松, 梁 红, 杨长生

(西北工业大学 航海学院, 陕西 西安, 710072)

长期以来, 混响强度计算主要采用基于简单的半经验性质的散射模型, 未能考虑环境参数。而实际上, 混响产生的过程中, 海底环境对混响至关重要。本文采用地声学海底交互模型(GABIM)将海底分为两层, 逐层计算界面散射和体积散射的散射截面, 得到海底散射强度的计算公式。在此基础上建立了一个海底混响强度随海底环境变化的单基地混响模型, 其采用单频信号仿真海底混响信号, 结果表明, 混响信号特性符合理论, 且改变环境参数混响也随之产生变化, 验证了该海底模型的可用性和环境适应性。

粗糙海底; 海底散射; 海底混响; 单基地混响

0 引言

我国领海大部分是浅海, 因此浅海作为水下活动中具有重要战略地位的区域, 日益受到人们的关注。浅海环境下由界面不平整性引起的界面混响更加显著, 导致混响强度提高, 从而加剧了混响干扰的严重性。实测结果表明, 浅海环境下, 海底散射强度远大于体积散射强度和海面散射强度, 同时由于浅海的负声速梯度的分布, 使得浅海海底混响成为影响混响强度的主要因素。

我国领海各区域的海底沉积层有很大的不同, 构成极为复杂[1], 有各种不同的分层情况及不同的地声学特性。长期以来, 混响研究主要采用基于简单的半经验性质的散射模型, 如Lambert模型计算海底混响[2]。这些散射模型一般计算简单, 但由于计算过程没有环境参数, 得到的混响信号缺乏相应的物理意义。而实际上, 混响产生的过程中, 海底环境对混响存在很大的影响。

国内外对复杂海底的散射模型做了很多研究, 模型主要包括两大类: Kirchhoff近似和小微扰理论、小斜率近似法(small slope approximation, SSA)[3-5]。利用SSA求解粗糙界面散射问题具有不受表面高度均方根条件限制等优点。虽然SSA结果在镜面方向是优秀的, 但在反向散射方向, 结果不是十分理想[6], 所以本文在单基地混响建模中使用第1类散射模型, 其研究以Jackson为代表。

Jackson等人对单基地与双基地海底散射做了大量研究。文献[7]等已有了利用Jackson双基地散射模型求解散射强度从而建立随环境变化的双基地混响模型的方法。然而对于单基地混响, 这种散射模型应用较少。为建立随环境变化的单基地混响模型, 本文引入Jackson单基地散射理论。

Jackson的单基地散射模型经过了一个较长时间的发展。1986年及之后几年提出的单基地海底散射模型[8-9], 应用Kirchhoff近似和小微扰理论, 将海底散射视为粗糙海底界面散射与沉积层体积散射之和。该模型为高频声波海底散射的物理过程提供了一个比较合理的描述, 然而该模型忽略了海底分层等因素的影响。2010年Jackson等人提出了一个地声学海底交互模型(geoacoustic bottom interaction model, GABIM)[10], 将海底散射推广到任意分层海底散射的情况, 深入考虑了来自沉积层界面的粗糙度散射以及介质的弹性效应, 优化了散射强度计算方法。因此本文使用GABIM散射模型研究单基地混响。

由于海底沉积物通常气体含量微少, 一般简化为海水饱和固液两相介质, 因此本文将海底分为两层。鉴于双基地混响建模方法中, 散射模型的散射强度可以直接使用, 本文同样直接使用GABIM计算散射强度, 建立基于射线理论的单基地海底混响模型, 对产生的混响信号的各种特性进行验证, 从而证实混响模型仿真方法的可用性。由于散射模型较全面地考虑了海底环境因素对散射强度及混响强度的影响, 实现了单基地混响模型对环境的适应性, 其预报结果比较准确。

1 海底散射模型

1.1 模型的定义和假设

对海底散射模型, 有如下假设条件:

1) 第1层和最后1层界面粗糙, 其他假定平坦。

2) 海底界面起伏为各向同性2D高斯随机过程。

3) 所有层是非均匀的, 存在体积散射, 且体积散射是各向同性的。

4) 海底沉积物为无损的流体, 不考虑其弹性和滞性的影响。

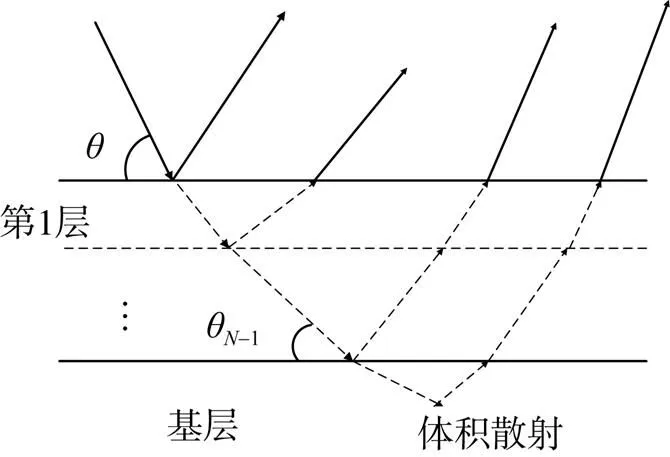
图1 分层海底声散射示意图

1.2 模型参数

海底底质参数主要包括: 海底界面粗糙度、沉积物类型、沉积物密度、压缩波波速衰减、切变波波速与衰减等。

GABIM沉积层体积散射为通过无量纲参数假定全方位的体积散射特征

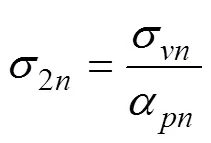
1.3 散射强度计算

GABIM模型的散射强度计算公式为

1) 沉积层-水粗糙界面散射

下面给出Kirchhoff、小粗糙度扰动和经验截面的插值算法

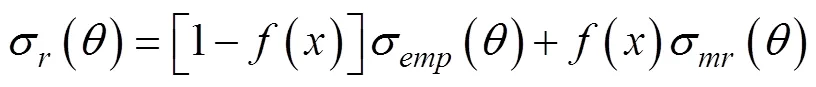
经验散射截面表达式为

对于水-沉积层粗糙度散射, Kirchhoff和小扰动截面使用下面的插值算法

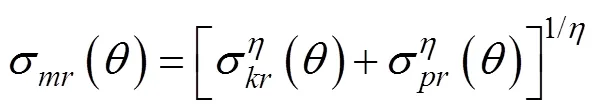
下面分别介绍Kirchhoff, 小粗糙度扰动方法的计算过程。

a. Kirchhoff近似法

b. 小粗糙度扰动近似法

根据理论研究和实测数据得到扰动近似法的表达式

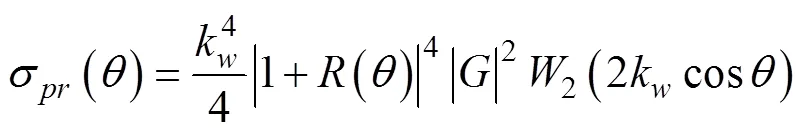
2) 基层粗糙度散射

对于基层粗糙度散射, 同样使用式(4)计算散射强度, 但需要改变其中的地声学参数, 使其适合于计算基层粗糙度散射。需要改变的参数包括声速, 密度和损失参数。

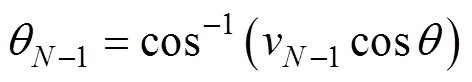
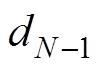
对Kirchhoff近似法, 反射系数在垂直入射方向估计, 下面为传输损失因数的计算。

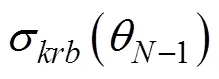
3) 体积散射

体积散射对截面的贡献是每层贡献之和。

对第层

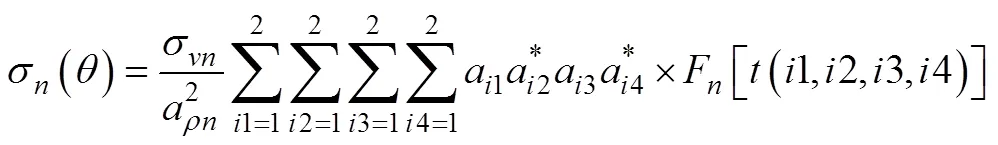
1.4 海底散射模型的仿真与分析

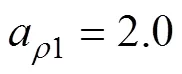
1) 取声波频率=1 kHz, 比较分层和不分层海底的散射。不分层海底忽略了基层粗糙度散射。

从图2可见, 在掠射角小于海水–沉积层临界角时2个模型的散射强度相同。在掠射角大于临界角时, 分层海底加入了来自基层的海底散射, 散射强度明显大于不分层海底。

图2 分层海底与不分层海底散射强度的比较

2) 取声波频率分别为5 kHz, 10 kHz, 20 kHz, 40 kHz, 散射强度采用GABIM模型计算。图3给出了散射强度随掠射角和频率的变化。从图3可见, 海底散射强度随掠射角的增大而增大, 且在小掠射角随着声波频率的增大, 散射强度也增大。

图3 海底散射强度随入射角的变化曲线

2 海底混响模型

2.1 模型框架

近年来，一些研究表明，索氏的“语言”实际上是科学主义的产物[20-21]。所谓科学主义，是指主张把自然科学的方法应用于人文社会科学在内的一切研究领域的观点。科学研究往往需要去除各种“杂质”的影响，索绪尔的语言学理论中含有科学主义的因素，他提出的变革方法就是要开展一场“同质化”运动”[22]364。这里我们有必要深究两个问题：(1)社会科学为什么要去除杂质，开展同质化运动？(2)社会科学是如何去除杂质，达到同质化这一目的的？

图4 海底混响模型示意图

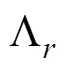
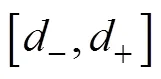
从而根据泊松分布确定散射体个数。

本文采用射线理论建立传播模型[11], 但并不影响散射模型仿真框架向其他混响建模方法推广。另外, 对混响过程做出如下假设: 1) 发射信号为窄带信号; 2) 声波在水中沿直线传播; 3) 忽略从海底反射到海面再被接收到的散射。

在上述条件限定下, 采用点散射结构, 单基地混响信号为

当声纳以速度匀速运动, 深度为, 基阵轴向与运动方向夹角为。则产生了多普勒频移, 混响信号的计算公式为

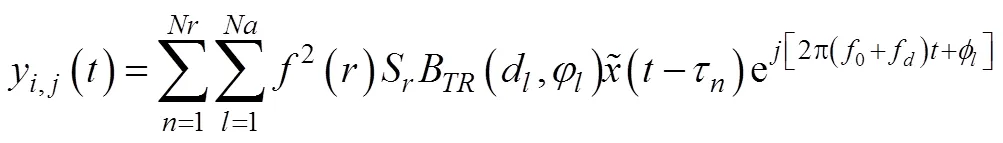
其中, 对于海底混响, 多普勒频移

2.2 海底混响仿真结果与分析

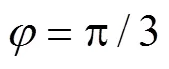
从图5中可看出, 海底模型的混响衰减基本符合混响级衰减曲线。

图5 GABIM混响信号时域图

图6中两图的对比可以看出, GABIM散射混响信号与原信号的频谱大致相同。符合混响信号频谱与发射信号频谱相似的理论。

图6 发射信号频域图与混响波形频域图

从图7可以看出, CW脉冲混响信号与发射信号自相关曲线包络具有一致的相关半径。结果符合自相关时间半径等于正弦信号脉宽的理论。理论分析表明, 泊松混响瞬时值服从高斯分布, 包络服从瑞利分布。从图8和图9可以看出, 仿真数据同理论较为吻合。

图7 发射信号和混响信号的自相关

图8 混响信号的瞬时值分布

图9 混响信号的包络值

对于建立的混响模型, 可以通过改变环境参数, 得到不同环境下的混响。理论上所有的环境参数都对混响有一定影响, 这些影响是存在于各方面的。本文选择比较容易观察到混响变化的参数来验证混响随环境的变化情况。由于混响时域比较有随机性, 故而选择频谱图来比较混响强度大小。

从图10可以看出, 改变声速比后频谱最大值为1时, 原来环境下的频谱最大值约为0.91。证明当第1层声速比变小后, 混响强度比原来增大。

图10 声速比改变前后的混响频谱图

从图11可以看出, 原环境参数的混响频谱强度最大值为0.24, 改变谱强度后混响频谱最大值是1。证明当第1层谱强度增大后, 混响强度增大, 海底表面起伏程度越大, 混响越强。

图11 谱强度改变前后的混响频谱图

通过上面对环境参数改变前后混响强度大小的比较, 验证了混响随环境参数变化的情况。

3) 若声纳沿信号发射方向运动, 速度为 20 m/s, 则接收的混响信号产生了多普勒扩展。对频率为20 kHz的信号, 其多普勒频移最大值为533 Hz, 信号在频域向更高频率展宽。使用2)的环境参数观察多普勒的影响, 结果如图12所示。

从图12可以看出, 在声纳匀速运动时, 接收的混响产生了一个宽度约为500 Hz的展宽。同时与无多普勒效应时类似, 海底界面起伏谱强度增大后, 每个频点的混响强度增大。

图12 运动声纳谱强度改变前后的混响频谱图

3 结束语

本文利用地声学海底交互模型求解粗糙海底散射截面, 建立了一个基于射线理论的混响模型, 对混响特性进行验证, 可以得出, 通过GABIM模型计算粗糙界面散射强度求得的混响, 其衰减、频谱及分布特性等与理论相符, 仍然满足统计规律。改变海底地声学环境参数, 其混响强度随之改变。从而这种更能适应海底环境改变的混响模型是可以建立的。此外, 分层散射模型还可以进一步扩展到沉积层体积散射各向异性的情况。

[1] 卢博, 李赶先, 黄韶健, 等.中国黄海、东海和南海北部海底浅层沉积物声学物理性质之比较[J]. 海洋技术, 2005, 24(2): 28-33.Lu bo, Li gan-xian, Huang shao-jian, et al. The Compare of Acoustic Physical Properties of the Subbottom Sediments at the Yellow Sea, the East China Sea and Northern South China Sea[J]. Ocean Technology, 2005, 24(2): 28-33.

[2] 刘伯胜, 雷家煜. 水声学原理[M]．哈尔滨: 哈尔滨工程大学出版社, 1993.

[3] Dashen R, Henyey F S, Wurmser D. Calculations of Acoustic Scattering from the Ocean Surface[J]. The Journal of the Acoustical Society of America, 1990, 310(88): 310-323.

[4] Thorsos E I, Broschat S L. An Investigation of the Small Slope Approximation for Scattering from Roughness Surface: Part I Theory[J]. The Journal of the Acoustical Society of America, 1995, 97(4): 2082-2093.

[5] Broschat S L, Thorsos E I. An Investigation of the Small Slope Approximation for Scattering from Roughness Surface: Part II Numerical Studies[J]. The Journal of the Acoustical Society of America, 1997, 101(5): 2615-2625.

[6] Thorsos Eric I, Jackson D R. Thirty Years of Progress in Theory and Modeling of Sea Surface and Seabed Scattering [J]. AIP Conference Proceedings, 2012 (127): 127-149.

[7] 张明辉. 海底声散射强度测量方法及不规则海域混响特性研究[D]．哈尔滨: 哈尔滨工业大学, 2011.

[8] Mourad P, Jackson D. High Frequency Sonar Equation Models for Bottom Backscatter and Forward Loss[J]. Oceans′89 Proceeding, 1989(4): 1168-1175.

[9] Moe J, Jackson D. First Order Perturbation Solution for Rough Surface Scattering Cross Section Including the Effects of Gradients[J].The Journal of the Acoustical Society of America, 1994, 96(3): 1748-1754.

[10] Jackson D R, Odom R I, Boyd M L, et al. A Geoacoustic Bottom Interaction Model(GABIM)[J].IEEE Journal of Oceanic Engineering, 2010, 35(3): 603-617.

[11] 苏绍璟, 郭熙业, 王跃科. 一种海底混响时间序列仿真方法研究[J]. 系统仿真学报, 2010, 22(8): 1853-1856. Su Shao-jing, Guo Xi-ye, Wang Yue-ke. Research on Simulation Method for Seafloor Reverberation Time Series[J]. Journal of System Simulation, 2010, 22(8): 1853-1856.

(责任编辑: 许 妍)

Modeling and Simulation of Monostatic Scattering and Reverberation for Rough Seafloor

WANG SongLIANG HongYANG Changsheng

(College of Marine Engineering, Northwestern Ploytechnical University, Xi′an 710072, China)

Reverberation strength calculation has long been based on the simple scattering model, which is semi-empirical in nature, without considering environmental parameters. In fact, environmental parameters impose important effects on reverberation generation. In this paper, the geoacoustic bottom interaction model (GABIM) is utilized to divide seafloor into two layers, and the cross-sections for interfacial scattering and volumetric scattering in each layer are calculated to obtain the formula of seafloor scattering strength. Based on GABIM, a monostatic reverberation model is set up, in which bottom monostatic reverberation strength depends on seafloor environment. Single frequency signal is adopted in this model to simulate the seafloor reverberation signal. The results indicate that the reverberation signal is consistent with the reverberation theory, and its strength changes with the environmental parameter.

rough seafloor; bottom scattering; bottom reverberation; monostatic reverberation

TJ631.2

A

1673-1948(2014)01-0060-07

2013-11-14;

2013-12-16.

国家自然科学基金(61273333)、(61379007).

王 松(1989-), 女, 硕士在读, 研究方向为信号与信息处理.