基于遗传算法的协同配送路径优化研究

曹庆奎，李言帮，陆 楠 CAO Qing-kui,LI Yan-bang,LU Nan

（河北工程大学 经济管理学院，河北 邯郸 056038）

(School of Economics&Management,Hebei University of Engineering,Handan 056038,China)

对于现代物流企业，如何降低营运成本、提高获利能力、优化运输路线成为物流管理的核心问题，直接影响和决定物流企业的核心竞争力。经济区域内，多物流中心各自根据客户要求选择配送路线的现象对于资源的利用率低、成本高，协同配送作为一种新的配送方式应运而生。协同配送就是把过去按不同货主、不同商品分别进行的配送，改为不区分货主和商品集中运货的“货物及配送的集约化”。也就是把货物都装入在同一条路线运行的车上，用同一台卡车为更多的顾客运货，有效地降低了营运的成本，提高了资源利用率和物流企业竞争力。

路径优化问题一直是学者们研究的热点，协同配送的配送方式的研究正处于初级阶段，Zhang等采用一种框架式的中央协调系统，同时配备一个多目标遗传优化的功能解决了在协同配送中订单分布的问题[1]。温惠英等用了模糊规划模型和算法，考虑车辆行驶时间和顾客服务时间的不确定性，建立车辆配送总费用最小的协同车辆路径问题模糊规划模型，使用了自适应离散粒子群算法求解了该问题[2]。李丁等基于虚拟企业与资源集成理论，提出在虚拟环境下第三方物流企业实施协同配送的模型，并用Automod仿真软件对该模型进行了仿真研究[3]。刘明等构建了一种混合协同配送模式兼顾了传统点对点配送模式和枢纽辐射模式的长处，给出了具体求解的启发式搜索算法，采用该模式能形成更加高效的应急救援网络[4]。杨韬等提出协同配送通过企业间资源共享、优势互补，能有效降低配送成本，增加收益。协同配送能否健康发展关键在于合作企业间的成本分摊与利益分配是否合理，综合考虑收益与成本提出了收益分配的新思路[5]。王新平等采用纵向配送和横向转运相结合的协同配送模式，构建了一类应急物流网络优化多目标随机规划模型[6]。综上所述，普通配送方式的路径优化的研究已经比较成熟，但是协同配送的物流配送方式的研究现在主要是对于利益分配机制的研究。对于协同配送的物流配送路径优化的研究很少，而且对协同配送的研究也主要是针对配送的成本降低展开的，对影响配送的其他方面的研究很少。

1 协同配送路径优化数学模型的描述及建立

本文结合普通物流配送路径优化的模型建立，以物流中心与客户为研究对象，遵从费用最小化原则，考虑双方在物流过程中所涉及的配送距离、车辆载重等问题，构建协同配送路径模型：

假设联盟中有M个物流中心 （m=1,2,…,M）向N个站点 （n=1,2,…,N ）配送货物，且每个物流中心只有一辆可用的车辆，每辆车的最大载重量为G，第n个站点的货运量为g（n），允许车辆进入站点的最早时间为St（n ），最迟时间为Et（n ），St（n）≤Et（n），卸货消耗时间为T（n ），客户n的坐标位置为 （xn,yn）；物流中心m的坐标为 （xm,ym），平均车速v（m ），调动车辆固定费用pf，车辆行驶每公里消耗费用pc。显然配送总费用为调用车辆固定费用与车辆运输费用之和，多中心协同配送调度的目标就是总费用Z最低。由此建立数学模型如下：

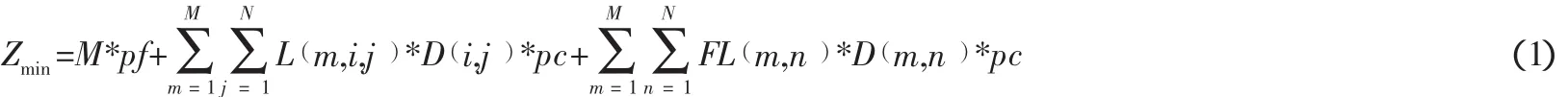
其中，S（ m,n）=1表示站点n由m中心配送，否则S（ m,n）=0；如果n是该车辆的第一站或最后一站（最后一站完成后返回m中心），FL（ m,n）=1，否则FL（ m,n）=0；L（ m,i,j）=1表示第m中心经i站点到达j站点（i≠j），否则L（ m,i,j）=0。D（ i,j）为两个站点i和j之间的距离，D（ m,n）为中心m和站点n之间的距离。

约束条件：

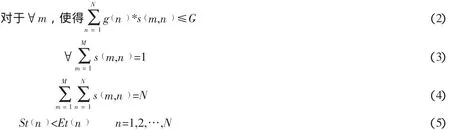
假设m中心进入第i站点的时刻为Tm,i，下一个站点为i+1，那么有下列约束条件：

2 基于多物流中心协同配送路径优化的遗传算法

2.1 算法描述

2.1.1 编码选择和初始群体建立

[8]阿兰·罗伯-格里耶：《理论有什么用》，《快照集/为了一种新小说》，余中先译，长沙：湖南美术出版社，2001年，第74页。

本文采用自然数编码的编码方式。m1,m2,…,mm为配送中心，随机产生n个客户的全排列1,2,3,…,n为各客户。这样可以编码m11 2 m1m13 4 5 6…n-1 n mm表示一种配送方案可行解。其中：m11 2 m1表示由配送中心对各户1和2进行配送任务，每个配送中心的配送必须满足模型建立中的约束条件，以此类推。各配送中心分别对自己的客户进行配送就可以表示出来。在编码选择配送中心的分配方式上将前一配送中心与下一配送中心结合，将其假设是一个配送中心，像m1m2变成m12，将m12m23m34…mn-1n先后顺序依次插入排列中保证相邻的两个之间都有客户，这样排列就变成m11 2 m123 4 5 m236…n-1nmm。按照这样的方法得到该问题的初始可行解也就是初始群体。

2.1.2 适应度函数

对于配送路径方案的评判，由于编码方法是根据车辆调度问题的特点确定的，其隐含每个客户都得到配送服务及每个客户仅由一家配送中心配送的约束条件，但是每辆车的载重限定为经过多次遗传操作后则不一定满足。因此适应度函数的确定要同时反映解的可行性与对应方案的费用。对于个体y，设其对应的配送方案的不可行路径数为My（My=0表示该个体为一个可行解），其目标函数值为Wy，则该个体y的适应度函数Fy可以表示为：

其中，pω表示每条不可行路径的惩罚权重（该权重在目标函数取值范围内可以取一个相对较大的正数）结合实际情况，此处采用pω为1 000。

2.2 遗传操作

2.2.1 算子的选择

在已知的必须满足要求的前提下随机选取p条初始种群（初始染色体），采用以上的编码方式对产生的初始染色体进行编码，利用比例选择的方法对种群进行采样。这里引入选择概率的概念，设种群规模为p，种群中的一个个体i的适应度函数值为Fi，则该个体被选择的概率为fi：

2.2.2 变异操作

本文在问题的解决过程中引入n-1个虚拟客户，虚拟客户与真实的客户一样在配送的过程中都有对货物运输的需求，时间窗的约束条件。但是其货运量为0，货物配送中消耗时间为0。所以引入虚拟客户用X表示，其货运量为0，允许车辆进入站点的最早时间St（X）=0，最迟时间Et（X）=0，卸货消耗时间T（X）=0。则配送方案就变成：m11 0 2 0 m1m23 0 4 0 5 0 6 0…0 n-1 n 0 mm。

在进行基因换（移）位时可能会出现客户由多个配送中心共同拥有，这样就让随机的一个配送中心进行配送，依次来实现配送中心的联合，实现协同配送。

2.3 算法步骤

步骤1：参数的初始化包括客户数目n，适应度函数值Fi，选择概率fi，每一代染色体个数p，迭代次数k。

步骤2：按照既定的编码方式随机的产生初始种群，确保每条染色体为一个可行解。

步骤3：计算个体适应度。

步骤4：利用比例选择法，计算每个个体被选择概率，最优个体替代较劣个体，实现最优个体保留。

步骤5：变异操作，引入虚拟客户进行基因移（换）位。计算每一代染色体的适应度函数值，保留最优染色体。

步骤6：结束条件是否满足，不满足转步骤3，满足输出满意解。

3 实证分析

本文取邯郸市中3个物流中心m1,m2,m3，分别负责为11个客户配送货物，客户的编号分别定义为1,2,3,…,11。物流中心m1负责客户1,4,5的配送，物流中心m2负责客户3,7,8,11的配送，物流中心m3负责客户2,6,9,10的配送。为了便于计算规定客户与配送中心的位置在x,y平面上表示出来，客户与配送中心的距离用他们的直线距离的十分之一表示。站点货物需求量、卸货消耗时间、时间窗约束、坐标位置等相关信息如表1所示。

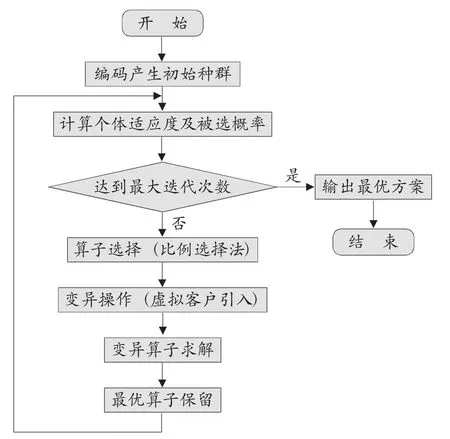
图1 遗传算法求解过程图

表1 配送客户货物及配送情况表

配送中心坐标分别为：m1（ 10,20）、m2（ 30,40）、m3（ 80,60）

由给定的配送中心及客户的坐标可以得出配送中心和客户距离如表2所示。

假设物流中心只有一辆车进行配送，最大载重为12t，平均车速为50km/h，单位历程费用为20元/km，车辆调用费用为100元，路径优化前配送路径及所产生的费用，如表3所示。

由表3可以看出配送中心m1和m2的车辆负载不够理想，需要协同配送。其中：配送中心m1发现客户1是一个比较孤立的个体，由配送中心m3对其进行配送所花费的配送费用更低。同样的客户11对于配送中心m2来说也是一个比较孤立的站点，由配送中心m3进行配送的情况下产生的运输费用会更低。因此，可以对3个配送中心进行协同配送，结合其中的2个配送中心选用其中的一个运输费用最低的进行配送会节约大部分成本。应用本文的协同配送调度算法，得出协同配送调度方案及成本，如表4所示。

表4中得到本问题协同配送后满意的解，对于普通的配送方式能够看出有明显的改进和优势。

由表3可知：总成本Z1=436+550+514=1 500（元）

总配送距离L1=60（km）

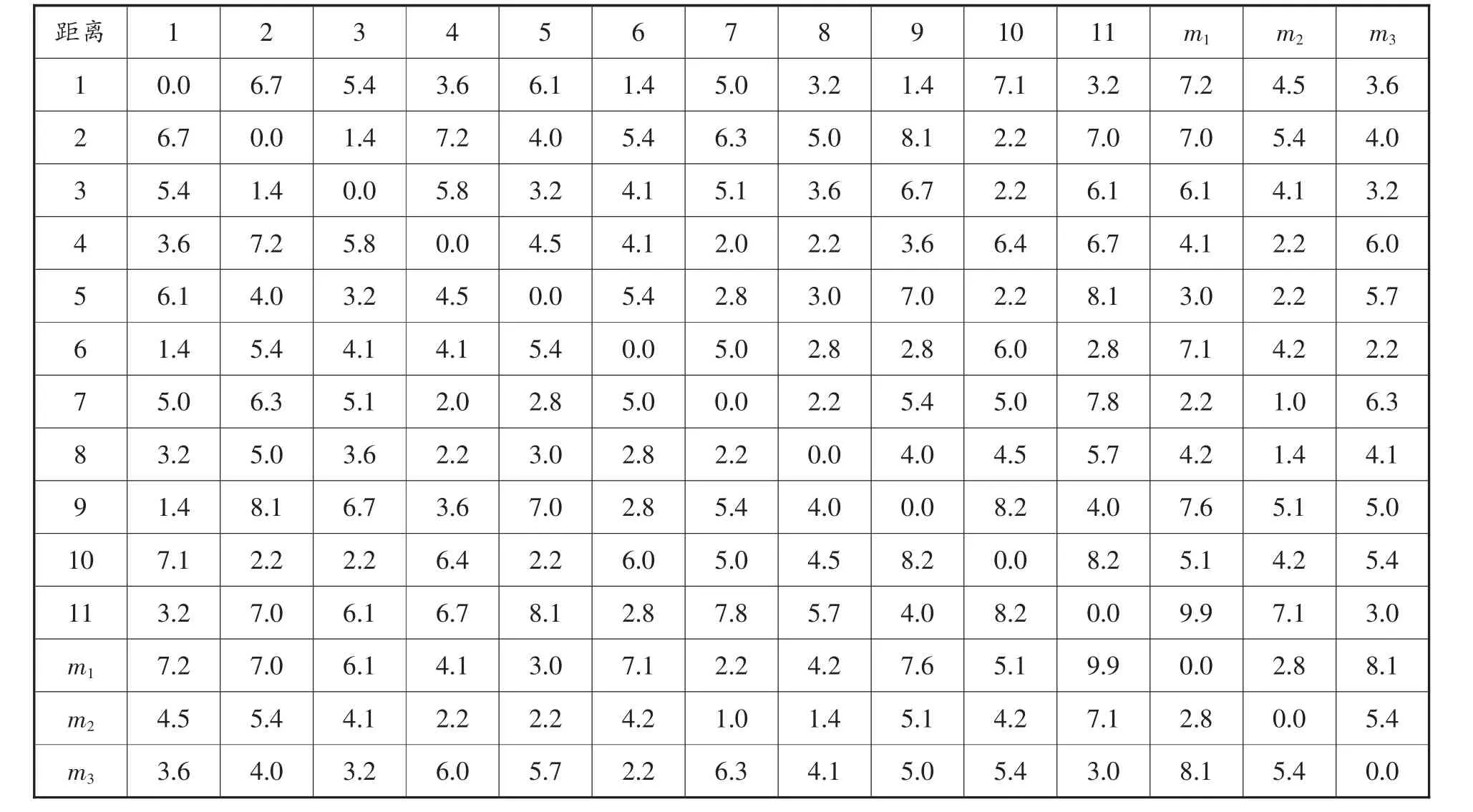
表2 配送和客户距离表 单位：km

表3 物流中心配送路径及费用表

表4 协同配送调度方案及成本表

由表4可知：协同配送后的总成本Z2=485+678=1 160（元）

总配送距离为L2=48（km）

总成本之差为z=Z1-Z2=1 500-1 160=340（元）

总配送距离之差为l=L1-L2=60-40=20（km）

由此可以看出，协调配送能够明显的降低营运成本，提高车辆利用效率，减少资源消耗。

4 结束语

针对普通物流配送方式运营成本高，资源消耗大的缺陷，构建了基于成本最小化的物流中心与客户的协同配送路径优化模型。在遗传算法对模型求解过程中引入虚拟客户的编码方式和基因换（移）位的基因变异方式，得出协同配送后最优的配送路径，为以后协同配送能够更好的实现，物流企业竞争力的提高，配送资源消耗的降低提供了一定的指导意义。

[1] Haixin Zhang,Yong Deng,Felix T.S.Chan,et al.A modified multi-criterion optimization genetical gorithm for order distribution in collaborative supply chain[J].Applied Mathematical Modelling,2013,37(14):7855-7864.

[2] 温惠英，孙博.协同车辆路径问题的模糊规划模型和算法[J].计算机应用研究，2011,28(2):442-444.

[3] 李丁，黄远新，田红英,等.虚拟环境下3PL企业实施协同配送的仿真研究[J].技术与方法，2009,38(7):117-120.

[4] 刘明，赵林度.应急物资混合协同配送模式研究[J].控制与决策，2011,26(1):96-100.

[5] 杨韬，王明华.协同配送中成本分摊和收益分配模型研究[J].科学技术与工程，2008,14(8):4033-4036.

[6] 王新平，王海燕.多疫区多周期应急物资协同优化调度[J].系统工程理论与实践，2012,32(2):283-291.