考虑工程约束的发动机悬置支架拓扑优化

朱剑峰，林 逸，施国标，陈潇凯

(1.北京理工大学机械与车辆学院,北京 100081；2.泛亚汽车技术中心有限公司,上海 201206)

前言

近年来，在汽车工业得到高速发展的同时，能源短缺和环境恶化的问题越来越突出，车辆的轻量化研究迫在眉睫。动力总成悬置的结构优化与轻量化必须达到结构的模态、强度、刚度、耐久性和NVH性能的要求，并且要有良好的制造工艺性。文献[1]中进行了多工况下的结构静动态联合拓扑优化技术的研究，实现了变速器结构性能的改善和结构的轻量化。文献[2]中初步尝试了将拓扑优化技术应用到汽车控制臂的结构概念设计中，对控制臂的结构进行多目标拓扑优化，并探讨了制造约束的应用，在结构的后续设计可行性中取得一定效果。文献[3]中通过拓扑优化技术对路试中失效的悬置支架进行了优化分析与改进设计，成功解决了支架开裂问题。因此，拓扑优化技术已经成为工程技术领域的一个热门课题，在各大整车厂商和零件供应商中得到重视，但如何在产品结构设计初期就引入拓扑优化技术并最终成功应用到实际中仍然是目前汽车结构设计中的一个难点。在动力总成悬置的结构设计问题上，传统的凭借工程经验的设计方法很难使结构同时满足悬置的静态和动态性能要求。在早期的发动机悬置结构概念设计过程中，利用拓扑优化技术可以找到性能最优的、最合理的产品材料分布。通过这项技术，能缩短产品开发设计周期，提高产品性能，减少物理样件生产和试验的次数。

本文中在产品设计初期将拓扑优化技术引入到发动机悬置的结构设计中，按照设计空间建立拓扑优化模型，并施加用ADAMS计算出的动力总成悬置系统多种工况下的载荷，利用拓扑优化技术，并考虑实际工程约束条件，得出多工况下结构加权柔度最小(即刚度最大)而固有频率最大的拓扑结构，再根据拓扑优化结果和结构实际安装要求，设计出发动机悬置支架的详细结构，最后对新结构进行分析计算。

1 悬置系统工况分析

1.1 动力学模型

为了研究动力总成悬置系统的受力情况，建立了力学模型和数学模型，其力学模型如图1所示。图中，系统的广义坐标为沿X、Y、Z轴的平动坐标x、y、z和其绕X、Y、Z轴的转动坐标α、β、γ。

动力总成悬置系统为多自由度振动系统，可利用多种方法建立系统的运动微分方程，如直接法、影响系数法、拉格朗日法和有限元方法等[4]，文中应用拉格朗日法建立动力总成悬置系统的数学模型，即运动微分方程：

(1)

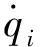
1.2 动力总成悬置系统工况

利用Motion View建立车辆动力总成系统动力学模型，同时综合考虑变速器悬置、前悬置、后悬置和发动机悬置橡胶衬套的刚度曲线，以及动力总成的质量、质心位置、转动惯量、变速器速比、发动机功率和转速等因素，最后，通过ADAMS求解器求解多体动力学模型，并输出动力总成在各悬置弹性中心点的载荷。考虑动力总成多种工况的对悬置结构的影响，采用GM动力总成悬置系统载荷计算方法[5]，输出多种动力总成悬置多工况载荷，包括常用工况和滥用工况，且能最大程度反映国内客户的实际使用情况，各种工况说明如表1所示。

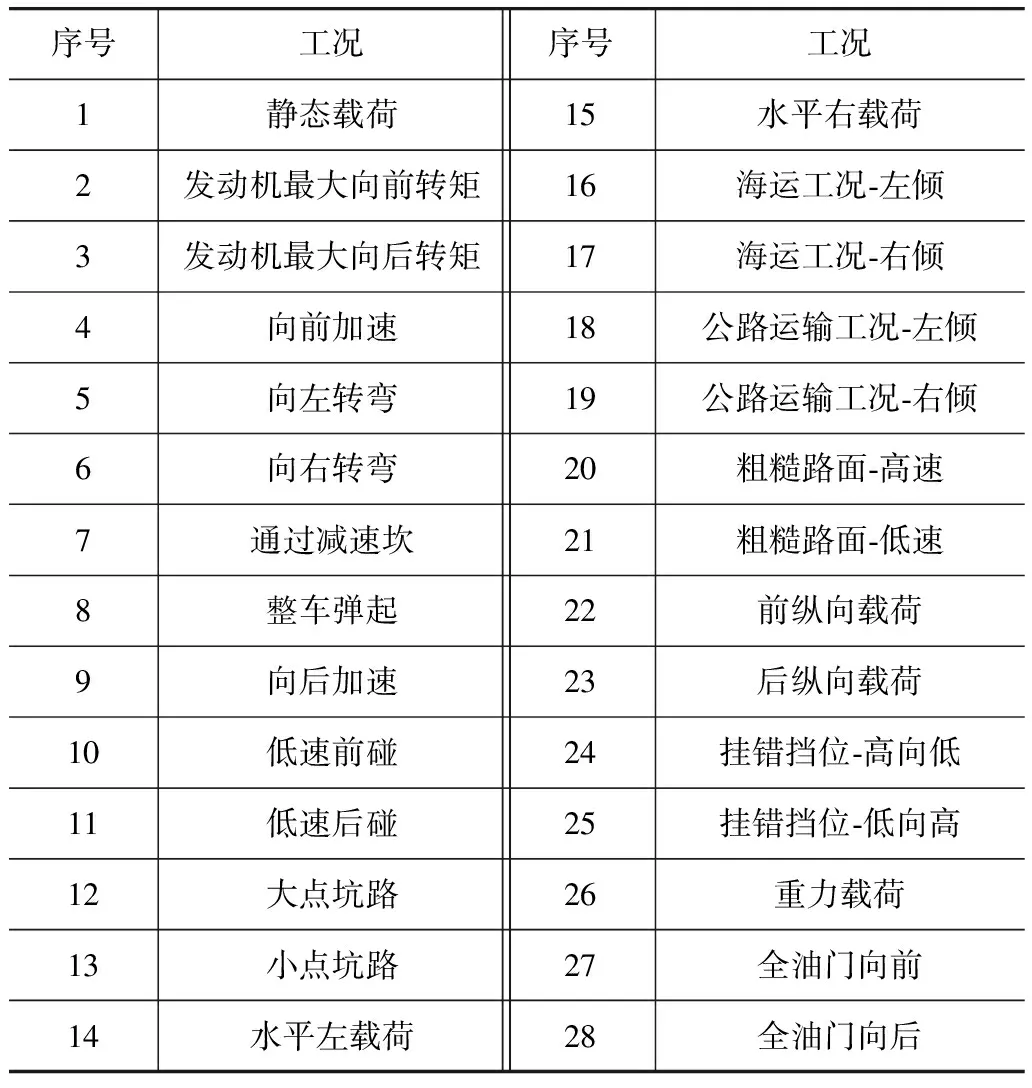
表1 动力总成悬置系统工况

2 拓扑优化方法

2.1 拓扑优化概述

目前，拓扑优化设计主要以单目标优化为主，例如静力学的刚度优化和动力学的特征值优化问题。常见的结构拓扑优化方法有变厚度法、变密度法和均匀化方法，而变密度法是当前比较简单有效的一种连续体结构拓扑优化方法，拓扑优化结果比较清晰，其程序简单、计算效率高，因此基于变密度法的拓扑优化方法在汽车行业得到了广泛的应用[6]。

2.2 工程约束下的结构拓扑优化方法

在实际的零件制造中，由于考虑到模具制造的问题，结构的最小尺寸必须满足加工制造要求，太小将很难甚至无法实现。拓扑优化结果往往不一定具备良好的加工特征，使优化结果难以制造甚至制造成本过高，因此在拓扑优化的数学模型中须加入工程约束，使拓扑优化结果在满足结构性能的要求下具有良好的制造工艺性。

最小尺寸的数学模型[7]表达式如下：

(2)

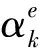
一致性方向控制的数学模型表达式如下：

(3)

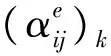
2.3 拓扑优化存在的问题

在进行拓扑优化过程中，采用密度插值模型虽能有效地压缩中间密度单元，但依然面临着数值稳定性的问题，如棋盘格(Checkerboards)和网格依赖性(Mesh-dependency)等问题[8-9]，另外动态拓扑优化由于各阶振型的互相切换，还面临着目标函数振荡问题。

综上所述，本文中在进行拓扑优化时，采用高阶单元和设置最小尺寸来控制棋盘格的出现和网格依赖性的问题，对于动态拓扑优化问题则采用模态追踪控制。

3 拓扑优化设计

3.1 拓扑优化模型的建立

根据悬置的结构特点，支架和发动机缸体连接的3个螺栓孔的连接刚度必须达到一定的水平，因为如果连接刚度不理想，很难拓扑优化出一个合理的结果，甚至优化失败。考虑发动机的整体布局，确定初始的优化模型如图2所示。图中，A为需要拓扑优化的部分，考虑到其上安装的惰轮载荷的不确定性，B部分和其余部分为非优化区域。

多工况静态优化是将各工况下柔度值进行加权，作为拓扑优化目标函数(即加权柔度最小)，以保证支架刚度最大化。同时提取非优化区域部分壳单元应力水平，并约束其最大主应力值小于160MPa，动态拓扑优化控制1阶频率最小值大于600Hz，拔模方向垂直于支架和发动机连接端面，最小开孔尺寸为3倍的单元平均尺寸。考虑到发动机端刚度足够大，将支架和发动机连接端的端面直接接地进行优化计算。

3.2 拓扑优化结果

经过静态和动态拓扑优化后的材料分布如图3和图4所示。静态、动态拓扑优化各经过了80次、40次迭代后收敛。

由图可见：考虑了工程约束下的发动机悬置支架结构在拓扑优化后的材料分布具有很好的加工工艺性，很容易将拓扑优化的结果转为详细设计模型；静态和动态优化在螺栓孔2处材料均发生堆积，说明提高该螺栓连接点的刚度可有效提高结构的整体刚度和模态，直接的加强筋布置可以参考拓扑优化后筋的走向，同时为了使该支架有很好的制造工艺性能，在布置加强筋时要控制壁厚在3～5mm，另外最小开孔尺寸不宜过小(大于10mm，否则模具设计比较困难)。

3.3 最终设计与性能分析

综上所述，根据静态和动态拓扑优化结果，同时参考其它竞争车型的悬置结构设计特点并结合实际工程开发经验，最后考虑结构的制造工艺性，发动机悬置结构最终设计如图5所示，最终质量为1.78kg。该支架采用铸铝AL380高压铸造，弹性模量为72.5GPa，泊松比为0.33，密度为2 700kg/m3，屈服极限为160MPa，抗拉强度为330MPa。

根据详细设计模型，对结构进行有限元验证分析，计算了结构在各工况下应力值，如表2所示，其危险工况为第18工况，应力分布如图6所示。

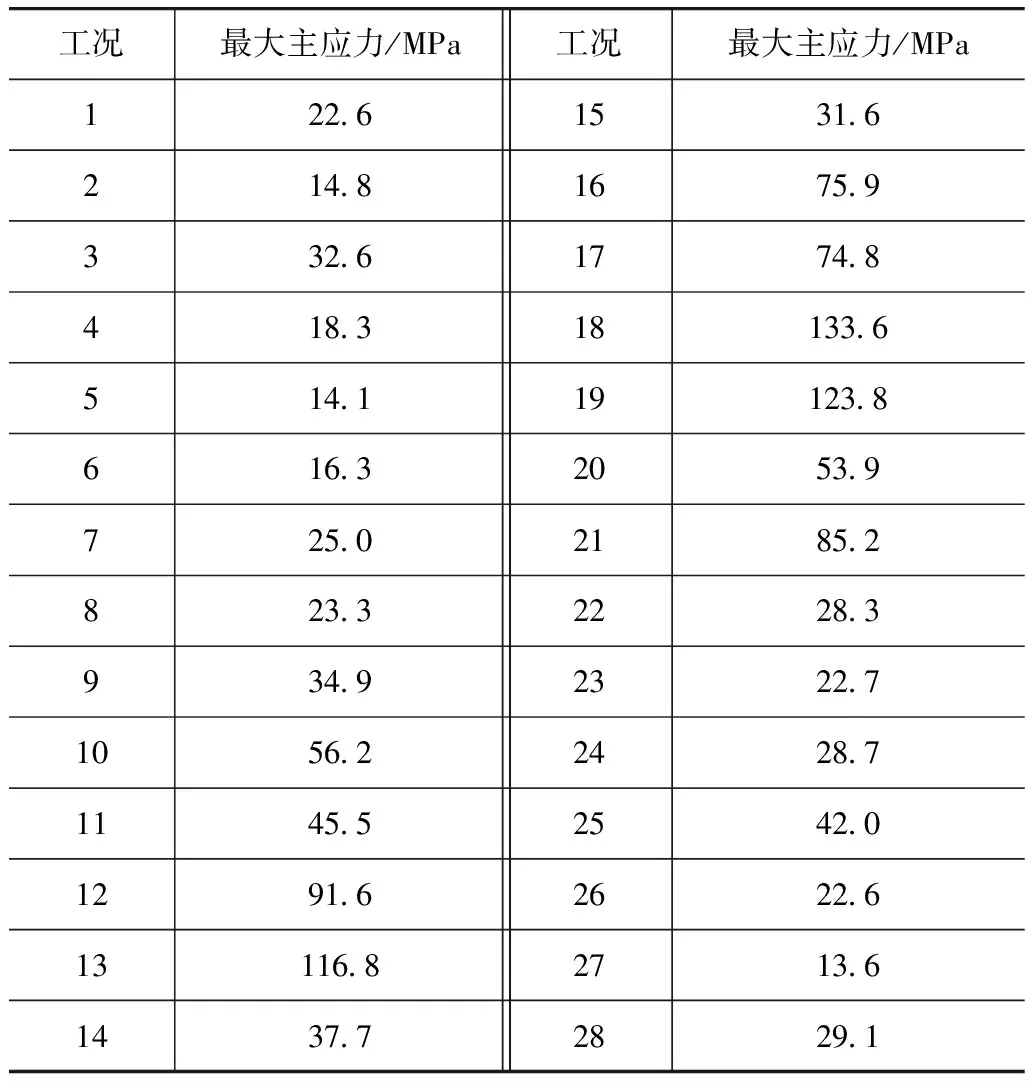
表2 各工况下应力结果

发动机悬置支架的固有模态结果如表3所示，对动力总成NVH性能影响最大的为结构的1阶模态，其对应固有振型图如图7所示。

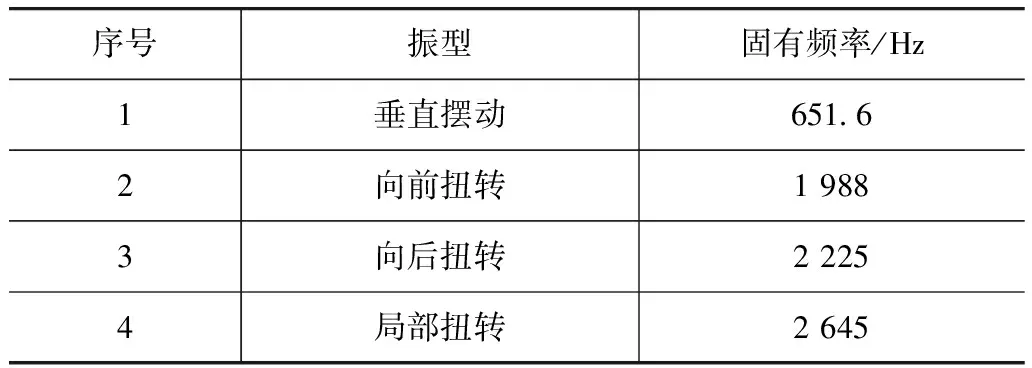
表3 各阶模态振型及频率

从以上分析结果可以看出，该结构在各工况下的应力水平均低于材料屈服极限，结构第1阶模态为600Hz，大于动力总成共振频率根据拓扑优化结果，在前期开发阶段即可设计出完全符合性能要求的发动机悬置结构，得到结构质量轻、性能优良的效果。

4 台架试验

在进行支架强度试验时，载荷利用MTS系列液压动作缸进行加载，液压动作缸通过定制的夹具和悬置衬套安装点进行连接，同时设置位移传感器，通过位移监控对台架试验进行安全保护，支架上的发动机安装点通过螺栓直接和刚性台柱联结在一起，为了避免零件的生产工艺等因素对试验结果的影响，对发动机悬置支架方案取3个样件进行结构的破坏性台架试验。根据发动机悬置支架的实际装配情况，搭建如图8所示的实物台架试验，由于该支架应力最大、最危险的工况所对应的力在Z向上达到最大，故单轴向台架试验主要针对Z向载荷进行试验验证(单轴向台架试验为结构的前期验证，最终的整车路试会针对28种工况进行结构性能验证)，设计目标根据工程经验为所有工况中Z向最大载荷的3倍(即11kN)，支架的最终台架破坏性强度试验时实际加载13kN。

从分析和试验结果来看，该支架完全满足结构强度要求，再次证明了拓扑优化结果的合理性和设计方案的可行性，发动机悬置支架的设计达到了预期的效果，为后续整车路试提供了保障。

5 结论

(1) 考虑工程约束下的结构拓扑优化结果具有良好的制造工艺性能，提高了拓扑优化结果合理性。

(2) 从计算结果可以看出，经过拓扑优化后设计出的发动机悬置结构应力降低，满足结构强度和耐久设计的要求，并且其1阶固有频率避开了动力总成共振敏感区，提高了产品的可靠性，降低了前期设计开发的风险和成本。

(3) 利用拓扑优化技术可以快速、合理地进行产品结构设计，避免了二次优化和再次改进设计。同时拓扑优化技术在车辆的轻量化设计方面有着重要的指导意义。

[1] 刘辉,项昌乐,张喜清.多工况变速器箱体静动态联合拓扑优化[J].汽车工程,2012,34(2):143-148.

[2] 祝小元,方宗德,申闪闪,等.汽车悬架控制臂的多目标拓扑优化[J].汽车工程,2011,33(2):138-141.

[3] 潘孝勇,柴国钟,刘飞,等.悬置支架的优化设计与疲劳分析[J].汽车工程,2007,29(4):341-345.

[4] 靳晓雄,张立军,江浩.汽车振动分析[M].上海:同济大学出版社,2006.

[5] 黄庆,杜登辉,黄小飞,等.动力总成悬置支架的多工况拓扑优化[J].汽车技术,2008(10):27-30.

[6] 赵红伟,陈潇凯,林逸.电动汽车动力电池仓拓扑优化[J].吉林大学学报,2009,39(4):846-849.

[7] Zuo Kongtian,Chen Liping,Zhang Yunqing,et al.Manufacturing and Machining Based Topology Optimization[J].International Journal of Advanced Manufacturing Technology,2006,27:531-536.

[8] Beckers M.Topology Optimization Using a Dual Method with Discrete Variables[J].Structural Optimization,1999,17:14-24.

[9] Sigmund O,Petersson J.Numerical Instabilities in Topology Optimization: A Survey on Procedures Dealing with Checkerboards,Mesh-dependencies and Local Minima[J].Structural Optimization,1998,16:68-75.