浅析《计算材料学》教学中的Hartree-Fock方法——以H2为例探讨Hartree-Fock方法

朱应涛张静林

（1.昌吉学院物理系 新疆 昌吉 831100；2.昌吉学院计算机工程系 新疆 昌吉 831100）

浅析《计算材料学》教学中的Hartree-Fock方法
——以H2为例探讨Hartree-Fock方法

朱应涛1张静林2

（1.昌吉学院物理系 新疆 昌吉 831100；2.昌吉学院计算机工程系 新疆 昌吉 831100）

在计算材料学和材料设计中，Hartree-Fock（HF）方法是重点，也是难点，虽然大多数教材中有相关的推导过程，但对学生来说却较难理解，对其实际应用也缺乏认识。本文以H2分子为例，讨论H2分子中HF方法的实现，对HF方法的推导过程和相关的物理图像加以阐释，使学生更好的理解HF方法及其应用，提高学生的学习兴趣。

Hartree-Fock；计算材料学；H2

计算材料学是材料学、计算机科学、物理和化学等多学科相互融合和交叉而形成的学科，随着计算机技术的发展和水平的提高，成为一门受到广泛关注的新兴学科。计算材料学涉及材料的各个方面，针对设计材料对性能的不同需求，有不同层次的材料计算方法，如量子力学方法、分子动力学方法、蒙特卡罗方法等。而其中的量子力学方法是材料设计中重要的手段之一，即通过了解材料体系的薛定谔方程，得到体系的能量和波函数，继而求力学量的平均值，最终达到了解材料物理、化学等性质的目的。对于物理专业的学生，虽有量子力学的基础，但量子力学本身就比较难理解，初等量子力学能求解的都是较为特殊的薛定谔方程（其中势函数比较简单），并且给出的都是解析形式的解。众所周知，对于多电子和多原子的材料体系，精确求解薛定谔方程是不可能的。另外，现在的教材［1］普遍的特点仅仅是公式推导，缺乏物理的图像，且推导过程有些也超出本科学生的数学能力范围。综上原因，计算材料学中的量子力学方法成为本课程的难点之一，为了让学生更好地理解求解的薛定谔方程的物理本质，有必要对量子力学方法中涉及的推导和物理意义加以讨论，本文将以H2为例探讨材料设计中的HF方法。

1 HF方法背景介绍

物质是由原子和分子组成，为了寻找微观粒子（电子、原子、分子）和宏观物质及其性能之间的关系，探讨宏观物质的微观物理机制，研究微观粒子的运动行为是必要的。在微观领域，经典物理的力学规律显的无能为力，自1900年由普朗克提出量子概念以来，量子力学成为研究微观粒子的重要手段。和经典力学中的牛顿方程相似，求解薛定谔方程（如方程（1））

是量子力学问题研究的重要内容之一，以此得到相应的体系波函数，进而得到材料的力学、热学、电学、磁学等性质。因此，微观机理和机制的研究最终成为对电子波函Ψ的薛定谔方程的求解问题。然而可以精确求解薛定谔方程的电子体系并不多，如H、类氢离子等，对于大多数体系，例如最简单的He原子、H2分子，都无法精确求解，只能通过各种近似方法（变分法、HF方法、DFT方法等）得到体系的近似解。随着计算机技术的发展，虽然HF方法在材料设计中逐渐失去了其显著地位，但是作为量子力学（或者量子化学计算）的思想的启蒙，在材料设计和量子力学相关的教材中占有重要地位。

对于多电子体系，虽然做了波恩-奥本海默（绝热近似）近似，将电子和原子核分开，分别求解电子和原子核的薛定谔方程，但是对于电子的薛定谔方程，由于电子和电子之间库仑相互作用项的存在，不能进行变量分离，所以还不能精确求解电子的薛定谔方程［2］。1928年，道格拉斯·哈特利（Hartree）为了求解多电子体系的薛定谔方程而提出Hartree假设，将电子看成是在由原子核和其他电子组成的势场中运动，将多电子问题转化成单电子问题。对于薛定谔方程中的哈密顿量则有独立的单个电子的算符算术加和而成，而对于体系的波函数就直接转换成了单个粒子波函数乘积的形式（Ψ=φ1（r1）φ2（r2）φ3（r3）...φn（rn）），其中所谓单粒子φi（ri）只是ri的波函数，|φi（ri）|2表示的物理含义就是第i电子在ri处的电子出现几率。所以，只要把每个粒子的波函数表示出来就可以得到多电子体系的波函数，然后需要通过求解H哈密顿量算符平均值可以得到体系的能量，当然也可以求解体系的其他力学量的平均值，进而得到相关的物理性质。以上是Hartree假设的基本思想。电子具有自旋，且自旋量子数是半整数，所以电子是费米子，而费米子的波函数要满足交换反对称性的，即如果量子粒子位置交换，波函数就会改变正负号，形如：（Ψ（r1，r2，r3，…ri，…，rj…，rn）=-Ψ（r1，r2，r3，…rj，…，ri，…，rn））。而Hartree提出的波函数，交换之后波函数不会改变符号，所以不满足交换反对称性。因此，在1930年，Hartree的学生弗拉基米尔·福克（Fock）和约翰·斯莱特（Slater）［3］分别单独将单电子波函数写成了Slater行列式的形式，如下面方程：

根据行列式的性质，如何交换行列式的任意两行或两列，行列式改变符号，如现将上式中的第一行和第二行交换，形式表现为单粒子波函数的坐标发生交换，而表现在物理上就是粒子1和粒子2位置发生改变，行列式改变符号，所以行列式满足交换反对称性，可以作为电子的波函数，接下来Fock和Slater将此行列式作为体系的初始波函数进行迭代计算，最终给出接近真实值的波函数，这就是HF方法。

2 HF方法推导

在量子力学中，求解体系的薛定谔方程，首先第一步要写出体系的薛定谔方程，只要将哈密顿算符写出即可。而由动能项和势能项组成，由量子力学知识可知，动能项，其中势能项是位置r的函数，根据点电荷的库仑定律可得，。因此对于一个多电子体系，通过绝热近似，原子核可以认为动能为零，故电子的薛定谔方程写为：

其中第一项是电子动能项，第二项是电子和原子核的相互作用势，第三项是原子核和原子核的相互作用，对于一个结构确定的体系，两个原子核之间的距离一定，所以第三项是一个常数，对波函数Ψ没有影响，所以对于确定的结构，此项可以省略。对于第四项，是电子和电子之间的相互作用势，正是由于此项的出现，使得波函数不再独立，不能进行变量分离，无法得到精确的解析解。（通常利用原子单位表示，？）将前两项单独写成单电子项：

而第四项写成双电子项：

因此多电子体系的薛定谔方程亦可写为：

体系的薛定谔方程已确定，下面将讨论如何求解此方程，即HF方法的推导。因为无法精确求解，HF方法将借助变分原理，给出了相应的HF方程。其中变分原理的思想就是首先通过试探波函数给出体系的能量，然后通过调整试探波函数寻找能量的极小值点。当体系的最小能量确定之后，体系的波函数随即也就得到了。

首先，给出体系的能量，前面我们已经提到了以行列式（2）作为初始试探波函数，给出能量值E：

其中dτ是包含位置r和自旋s的单位体积元。

其次，将行列式展开，根据行列式的性质，N阶行列式可以展成N！项形式，得到：

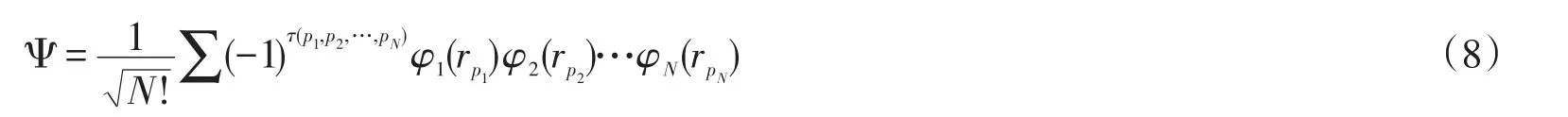
其中τ(p1,p2,…,pN)是粒子位置的互换，根据排列组合原理，N个粒子做位置变换并且排序共有N！种可能，所以Ψ由N！项连乘和的形式构成。

再次，将上述展开式子（8）带入方程（7），进行积分整理。在积分之前，我们先看几个积分：

a.单电子波函数正交归一，

这里积分变量空间坐标可以是r1，r2或者任意ri，但是积分结果是一样的，所以我们直接用1或者2表示坐标。

除了空间坐标之外，还有自旋坐标。对于自旋量子数ms=±1/2，对应波函数α和β两个态，满足：

所以连个自旋相关波函数的积分取决于ms，可以写成δ（ms1，ms2）。

b.单粒子算符hi的积分，即

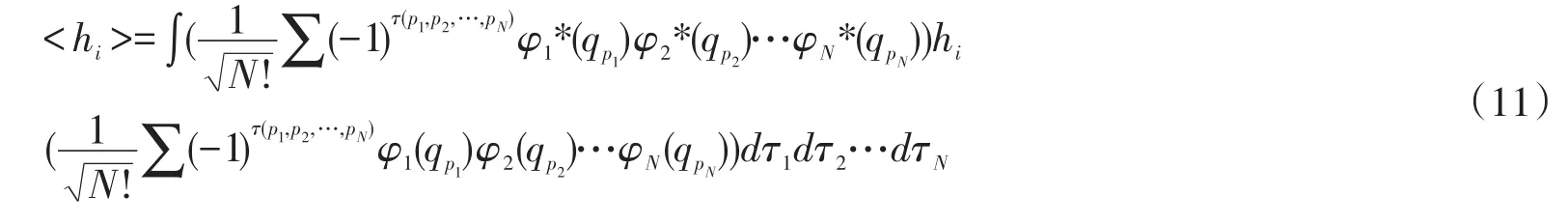
取出其中一项，如

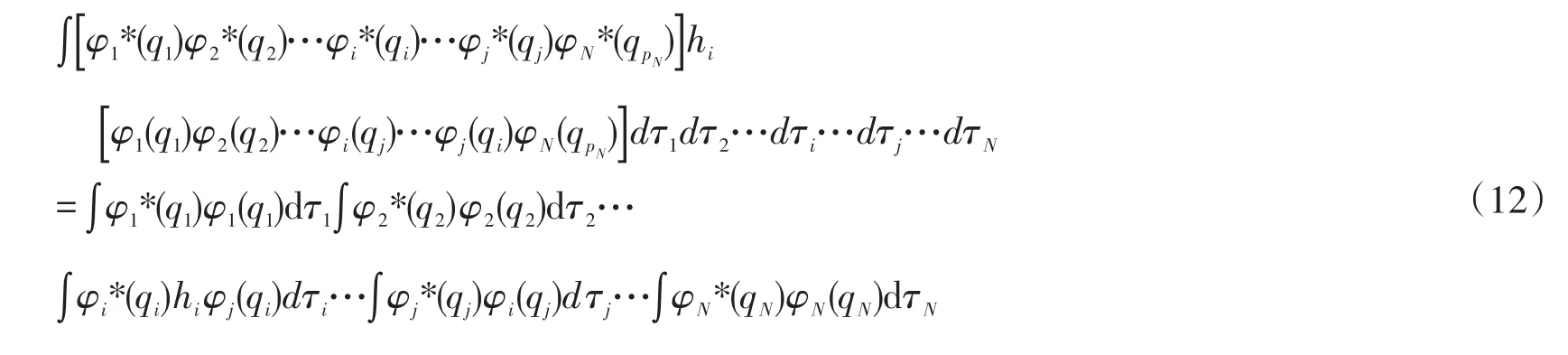
式中∫φ2*(q2)φ2(q2)dτ2项，因为自旋量子数相同，并且空间波函数的正交归一，此项等于1，不同项：

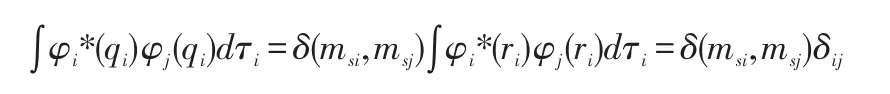
此处i肯定不等于j，δij=0，所以上式为零，所以只有当i=j时，才不为零，也就是积分项只能φ1(qp1)φ2(qp2)…φN(qpN)和其共轭项求积分才不会为零。因为有N！项位置的交换，所以这样的项就有N！项，所以＜hi＞可以表示成：，因为积分变量ri对积分值没有影响，故亦可化简成

c.双电子积分＜hij＞

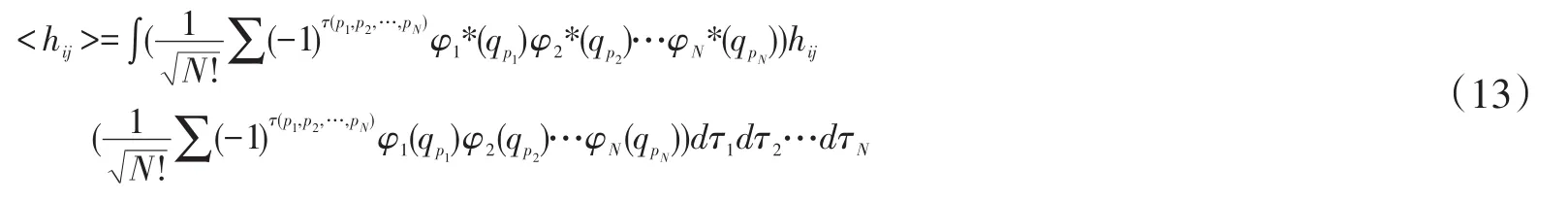
同样的取其中的一项，

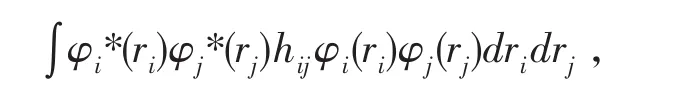
亦可写成：

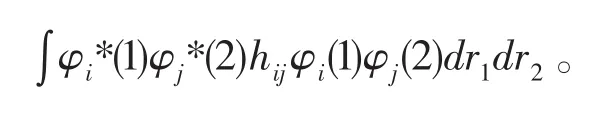
由于行列式的特点，还有一项与之相对，交换坐标qi和qj，是负值的形式出现。

所以最终双电子积分＜hij＞可以写成：

结合上述积分，可以将E的形式化为：

此处详细的推导结合H2，将在下面给出。

3 推导H2的HF方程

4 结论

在计算材料学中，虽然HF方法目前运用较少，但是其重要的物理思想不容忽视，所以目前有关计算材料学的很多教程中都有HF方法的推导的介绍，但是步骤都比较简略，其中涉及到的相关行列式和积分处理学生很难理解。本文就HF方法做了比较详尽的推导，且得到HF方程的非正则形式。本文以比较简单的H2体系为例，直观地给出了行列式，然后运用积分处理方法，导出其HF方程。期望材料相关专业的学生借助此文更深入的理解HF方法。

［1］张跃，谷景华，尚家香等.计算材料学基础［M］.北京：北京航空航天大学出版社，2007.

［2］I.LEVINE.Quantum Chemistry［M］.USA：Pearson Eduction，2011.

［3］JC.Slater.A Simplification of the Hartree-Fock Method［J］.Phys Rev，1951，81（3）:385-390.

G642

A

1671-6469（2014）04-0077-08

2014-06-05

朱应涛（1982-），男，山东淄博人，昌吉学院物理系，博士，研究方向：光催化材料基础研究。