悬挂参数对出口车辆动力学性能的影响

邱飞力，张立民，张卫华

（西南交通大学牵引动力国家重点实验室，成都 610031）

由于轨道的各向不平顺，车辆在行驶过程中产生随机振动，这种振动引发的车轮动载荷变化效应，影响列车的运行稳定性和舒适性。运行稳定性最直接的评价指标是蛇行失稳临界速度，是列车安全运行需要首先保证的动力学性能[1]。随着运行车速的提高，在曲线外轨上设置超高来平衡离心力，这样原直线和曲线的轨道构造就不完全相同，加剧车辆的振动[2]；与此同时，高速使得来自线路的激扰力加大，使得车辆振动加剧，影响车辆运行的平稳性[3]。出口列车采用了新的轮缘和轨道外形，轨距为米轨，与国内列车的轮轨均不相同，因而探究其动力学性能，确保运行的安全性和舒适性显得尤为必要。

1 力学方程

弹性车体上任意一点的广义坐标可以表示为[4]

它由6个刚体位移坐标和m阶模态坐标组成，x,y,z是局部坐标系在总体坐标系中的位置；ϕ,θ,φ是局部坐标系在总体坐标系中的欧拉角；qi是模态振型。R,Ψ是各坐标系中矢量表达，q是弹性模态振型向量[5]。

系统的动能T、势能W及能量耗散Γ分别为

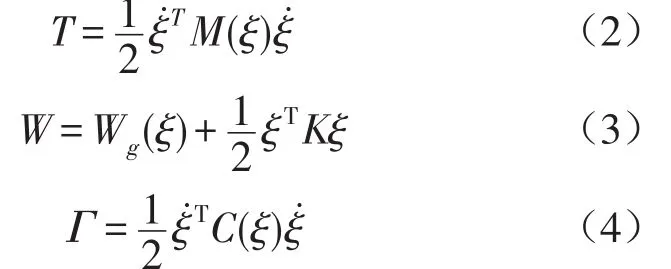
式中M(ξ)为系统的质量矩阵；Wg(ξ)为重力势能，K,C分别为对应模态坐标q结构部件的广义刚度矩阵和阻尼矩阵。

对具有r个完整约束的弹性体系统，应用拉格朗日方法可以得到该弹性体的动力学方程[5，6]

式中是拉格朗日函数，定义为L=T-W；λ是约束方程ψ的拉格朗日乘子；Q是广义力矩阵。

将（2）—（4）代入（5）可得弹性体方程式

式中fg是重力。

2 仿真模型

车辆系统是一个比较复杂的系统。在仿真分析中，对主要关注的参数尽可能做出符合实际，次要因素可以进行一些相应的简化。因此，建立以车体为柔性体的刚柔耦合模型车辆系统动力学模型。

首先在有限元软件ANSYS中对整车进行建模，采用Guyuan缩减[7]理论进行自由度缩减并求解模态，车体有限元模型如图1。利用Simpack与ANSYS接口程序将弹性车体导入仿真模型[8]，车辆刚柔耦合动力学模型如图2。

图1 弹性车体有限元模型

图2 车辆刚柔耦合动力学模型

刚柔耦合模型主要包括1个弹性车体，2个构架、4个轮对、8个转臂以及柴油发电机组、车体6个自由度，总共46个自由度。

该出口车辆建模所用的主要初始参数如表1所示。

表1 出口车辆模型初始参数表

3 运行稳定性分析

运行稳定性最直接的评价指标（蛇行失稳速度）是临界速度，是高速列车安全运行需要首先保证的动力学性能[1]。临界速度有两种分析方法，极限环分析方法和结构临界速度分析方法[9]。

结合poincare’提出的点射概念[10]，系统每一个的轨迹的后继点Qi的坐标为Si，其后继函数为Sk+1=f（Sk），若轨迹封闭存在极限环，后继函数线性表示为[11]

为了得到准确的非线性和分叉图，需要给列车加足够长时间和足够大的随机激扰，然后去掉激扰让列车运行到稳定的振动或平衡状态[12]。通过simpack仿真计算非线性临界速度时，先给予一段轨道激励，然后观察车辆在平直轨道上的仿真过程中横向振动是否能够快速收敛，收敛与发散的临界速度即为非线性临界速度[13-14]。在非线性临界速度下，轮对横向位移既不衰减，也不放大呈等幅稳态振动[15]。

不同的一系、二系悬挂刚度下，计算出口车的临界速度。车辆的临界速度随一系和二系垂向刚度变化趋势分别如图3和图4所示。

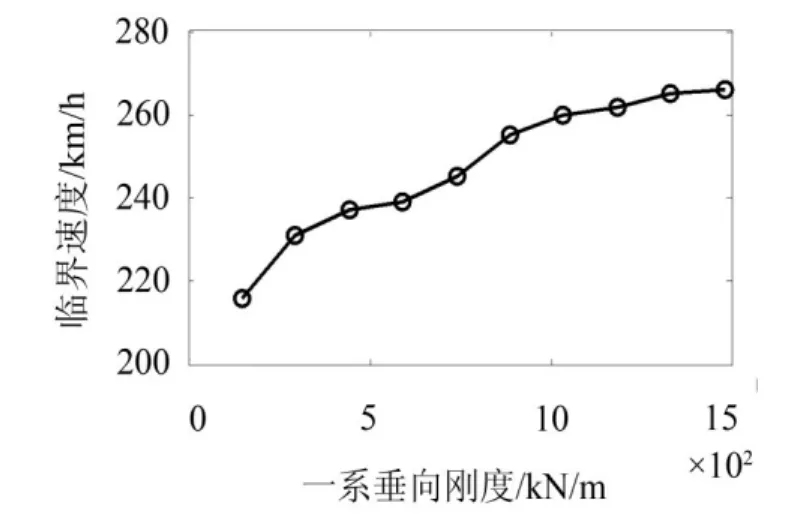
图3 临界速度随一系垂向刚度变化趋势图

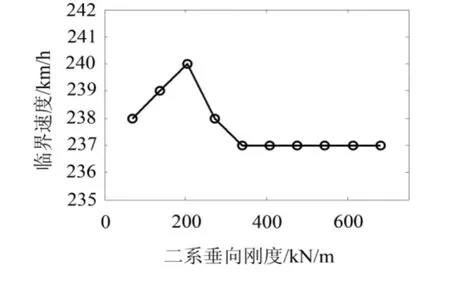
图4 临界速度随二系垂向刚度变化趋势图

从图3和图4可以得出，一系垂向刚度从150 kN/m线性增加到1 500 kN/m,车体的临界速度从216 km/h逐渐上升至266 km/h；二系刚度从68 kN/m线性增大到680 kN/m过程中，二系垂向刚度为204 kN/m时，车辆的非线性临界速度最大；二系垂向刚度大于340 kN/m时，二系垂向刚度增大对车辆临界速度不再产生影响。

4 悬挂系统参数对平稳性的影响

铁道车辆的运行品质是评价车辆动力学性能的重要指标之一，而运行平稳性指标是对旅客乘坐舒适性的评价，也是对客车的运行品质的评定[16]。目前，国际上采用较多的有两种评价方法，UIC sprling评价方法和ISO 2631标准，包括三分之一倍频和总的加权值评价法[17，18]。对该出口车型平稳性计算，采用ISO 2631国际标准。该标准以某一方向上所有加速度均方根值作为评价指标，如（10）所示[19，20]。

aw为频率计权加速度，Wi为给定的第i个1/3倍频带中心频率对应的计权因数;ai为第i个1/3倍频程带的均方根加速度。

车辆在不同的运行速度下，按标准测取空气弹簧座上方地板的振动加速度，结合式子（10）计算其平稳性指标。

一系垂向刚度变化对车辆横向和垂向平稳性指标的影响分别如图5和图6。

图5 横向平稳性随一系刚度和速度变化趋势图

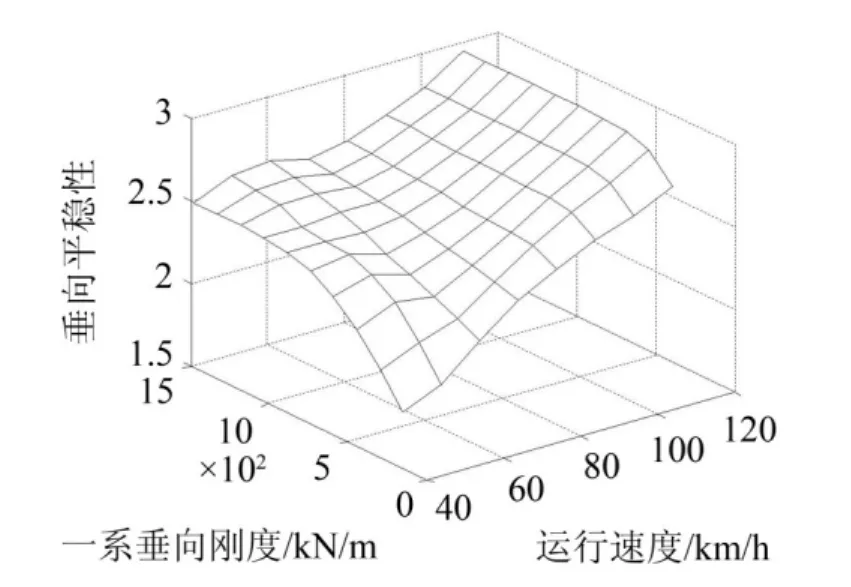
图6 垂向平稳性随一系刚度和速度变化趋势图

由图5和图6可知，列车速度小于60 km/h时，同一速度下横向、垂向平稳性指标随着一系刚度的增大而增大；速度大于60 km/h时，同一速度下一系垂向刚度对横向、垂向平稳性指标影响较小。一系垂向刚度小于750 kN/m时，横向平稳性指标随着速度增大而增大；一系刚度大于750 kN/m时，横平稳性指标在速度60 km/h时最小，速度大于60 km/h随着速度递增。不同一系刚度下，垂向平稳性指标随着速度增大而增大。

二系垂向刚度变化对车辆横向和垂向平稳性指标的影响分别如图7和图8。

不同速度下，二系垂向刚度对列车横向平稳性指标影响较小；列车速度大于70 km/h时，横向平稳性指标随着运行速度增大而增大。列车速度低于60 km/h时，垂向平稳性指标随速度增大而增大，受二系垂向刚度影响较小；列车速度高于60 km/h时，二系刚度在200～400 kN/m范围内垂向平稳性指标较小，二系刚度在400～800 kN/m范围内，垂向平稳性指标受二系影响较小且随着速度提高而增大。

一系垂向阻尼变化对车辆横向和垂向平稳性指标的影响分别如图9和图10。

图7 横向平稳性随二系刚度和速度变化趋势图

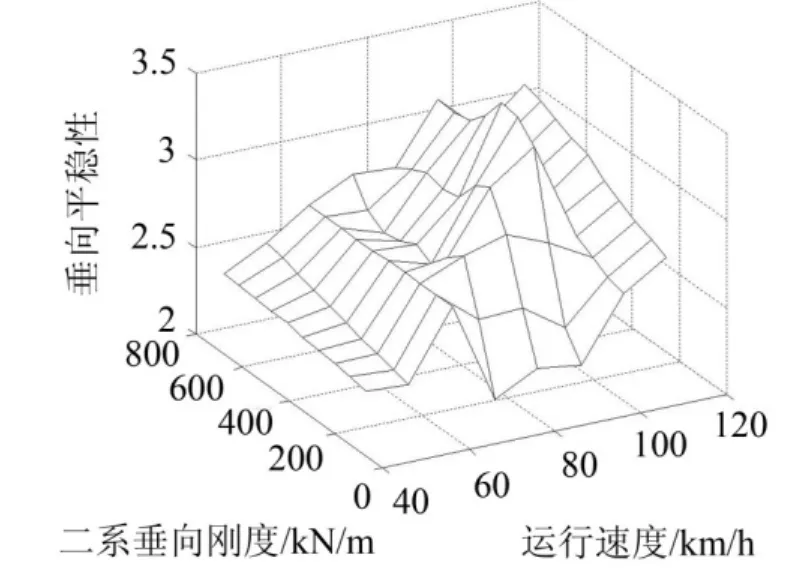
图8 垂向平稳性随二系刚度和速度变化趋势图

图9 横向平稳性随一系阻尼和速度变化趋势图

图10 垂向平稳性随一系阻尼和速度变化趋势图

不同速度工况下，横向平稳性指标和垂向平稳性指标受一系垂向阻尼影响较小。列车在60 km/h速度下运行，横向、垂向平稳性指标最小；大于60 km/h速度时，平稳性指标随着速度增大而增大。

二系垂向阻尼变化对车辆横向和垂向平稳性指标的影响分别如图11和图12。

图11 横向平稳性随二系阻尼和速度变化趋势图

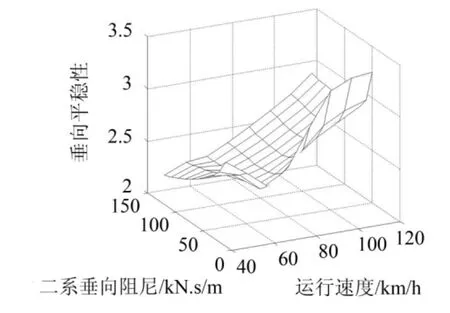
图12 垂向平稳性随二系阻尼和速度变化趋势图

横向平稳性指标在60 km/h速度下最小，大于60 km/h速度时，横向平稳性指标随速度增大而增大，且受二系垂向阻尼影响较小。垂向平稳性指标整体上随着速度增大而增大，随阻尼减小而出现增大趋势。阻尼为于75 kN.s/m时，垂向平稳性指标最小；阻尼大于75 kN.s/m时，垂向平稳性指标基本保持不变。

5 结语

(1)一系垂向刚度在150 kN/m～15 00 kN/m范围内，车辆的非线性临界速度随一系垂向刚度增大而提高。二系垂向刚度在68～680 kN/m范围内变化，当其取值为204 kN/m时，车辆的非线性临界速度最高。一旦二系垂向刚度大于340 kN/m时，临界速度基本保持不变；

(2)车辆横向平稳性受一、二系垂向刚度和垂向阻尼的影响较小，在60 km/h速度时取得最小值。车辆运行速度大于60 km/h时，横向平稳性指标随着车速增大而增大；

(3)垂向平稳性受一系垂向阻尼影响较小，随着速度提高而出现增大的趋势。垂向平稳性随二系垂向阻尼增大而减小，当二系垂向阻尼大于75 kN s/m后，垂向平稳性基本不变；

(4)当列车速度低于60 km/h时，一系垂向刚度越大平稳性越大，二系垂向刚度对垂向平稳性影响较小。列车速度高于60 km/h时，一系垂向刚度对垂向平稳性影响较小。二系垂向刚度对垂向平稳性影响较为复杂，但二系垂向刚度小时垂向平稳性较小。

[1]王福天.车辆系统动力学[M].成都：西南交通大学出版社，1994.

[2]张健全，黄运华，李芾.缓和曲线线型对铁道车辆动力学性能的影响[J].交通运输工程学报，2010，10(4)：39-44.

[3]张曙光.高速列车设计研究方法[M].北京：中国铁道出版社，2009.

[4]邬平波，薛世海，杨晨辉.基于弹性车体模型的高速客车动态响应[J].交通运输工程学报，2005，5(2)：5-8.

[5]宫岛，周劲松，孙文静.高速列车弹性车体与转向架耦合振动分析[J].2010年全国铁路机车车辆动态仿真学术会议论文集，2100，12.

[6]李世亮，王卫东.考虑车体弹性的铰接式高速车辆模型及响应计算分析[J].中国铁道科学，1997，18(2)：77-85.

[7]Guyuan R J.Ruduction of stiffness and mass matrices[J].AIAAJournal,1965,2:1133-1145.

[8]李原辉.高速列车模态匹配与悬挂参数分析研究[D].成都：西南交通大学，2012.

[9]黄运华.120 km/h B型地铁车辆动力学性能研究[J].机车电传动，2009，(5)：27-29.

[10]王海期.非线性振动[M].北京：高等教育出版社，1992.

[11]张卫华.机车车辆动态模拟[M].北京：中国铁道出版社，2006.

[12]梁树林，朴明伟，等.高速列车横向稳定性的非线性影响因素研究[J].铁道学报，2009，31(5)：24-30.

[13]罗仁，曾京.列车系统蛇行稳定性分析及其与单车模型的比较[J].机械工程学报，2008，44(4)：184-188.

[14]刑露露，李芾，符政波.弹性车轮车辆临界速度及曲线通过性能分析[J].电力机车与城市车辆，2012，35(1)：25-29.

[15]王开云，翟婉明，封全保.机车牵引状态下曲线通过导向特性研究[J].中国铁道科学，2006，27(3)：71-76.

[16]铁道车辆动力学性能评定和试验鉴定规范GB/T 5599-1985[S].CN-GB 2004.

[17]焦俊芬.客车运行品质评定中应用ISO2631标准的研究[J].铁道机车车辆，1995，(4)：36-41.

[18]万里翔,许明恒.铁道车辆运行平稳性评价方法的研究[J].铁道机车车辆，2001，(1)：8-11.

[19]ISO 2631/1-1985 Guide for the evaluation of human exposure to whole-body vibration［S］.

[20]刘转华.铁道车辆运行平稳性评价方法研究[D].成都：西南交通大学，2012.