凸函数在一些证明题中的应用

尹红然

（天津天狮学院 公共基础教学部，天津 301700）

凸函数在一些证明题中的应用

尹红然

（天津天狮学院 公共基础教学部，天津 301700）

本文介绍凸函数在证明詹森（Jensen）不等式、霍尔得（Holder）不等式、闵可夫斯基（Minkowski）不等式、哈达马（Hadamard）定理的简单应用。

凸函数；不等式；Jensen不等式

凸函数是高等数学及数学分析中的一个重要概念。凸函数本身有着许多很好的性质，掌握和利用好这些性质，能是一些较复杂的问题简单化。本文通过几个实例来说明凸函数在数学分析的一些证明题种的应用。凸函数的定义在不同版本定义有差别，本文采用的定义1：设f（x）在区间I上有定义，f（x）在I上称为凸函数，当且仅当：∀x1，x2∈I，∀λ∈（0，1）有f（λx1+（1-λ）x2）≤λf（x1）+（1-λ）f（x2）.

一、利用凸函数证明詹森（Jensen）不等式

若f（x）为区间I上的凸函数，则对任意

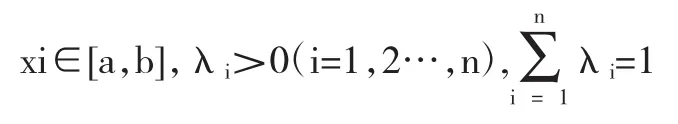
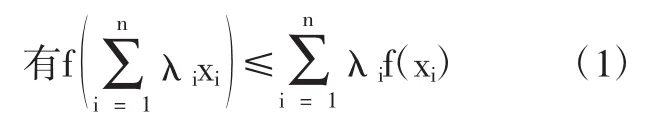
证：应用数学归纳法.当n=2时，由定义1命题显然成立。

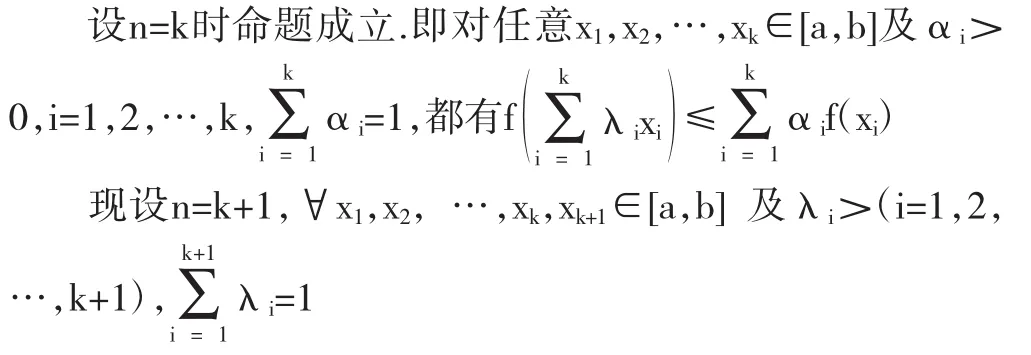
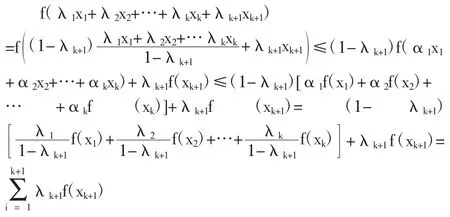
这就证明了对任何正整数n（≥2），凸函数f（x）f总有不等式（1）成立。

二、利用凸函数证明霍尔得（Holder）不等式

由Jensen不等式知（4）式成立，从而结论成立。

三、闵可夫斯基（Minkowski）不等式

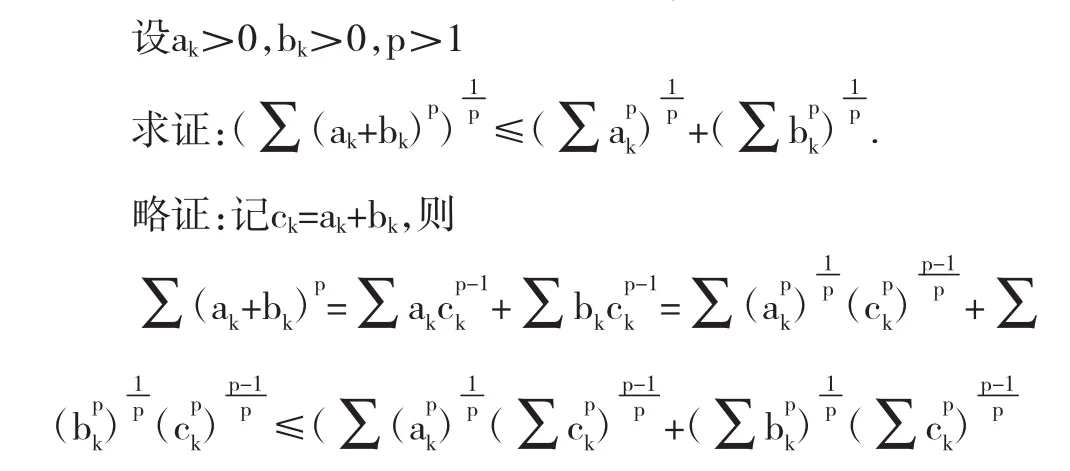
此不等号利用Holder不等式

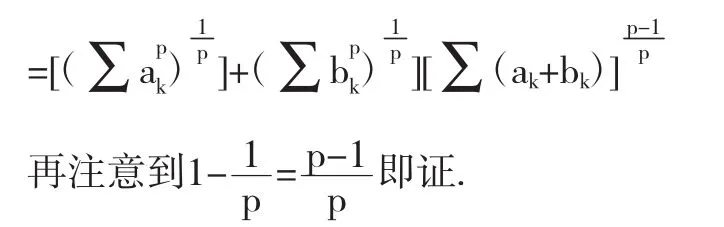
此不等式又称为距离不等式.当p=2，n=3时此式表示三角形中任意一边小于另两边之和，此又称三角不等式。

四、利用凸函数证明哈达马（Hadamard）定理

设f（x）为区间[a，b]上的连续凸函数.试证：∀x1，x2∈[a，b]，x1＜x2，有

值得注意的是Hadamard定理的几何意义非常明显：当f（x）＞0时，曲线f（x）在[x1，x2]上的面积，不小于过点的任一直线在[x1，x2]的面积，不大于点（x1，f（x1））与点（x2，f（x2））间的弦在[x1，x2]的面积。

[1]林源渠.数学分析习题集[M].北京：高等教育出版社，2001.

[2]姜东平，等.数学分析教程[M].南京：南京大学出版社，2000.

[3]朱时.数学分析札记[M].贵阳：贵州省教育出版社，1994.

[4]裴礼文.数学分析中的典型问题与方法[M].北京：高等教育出版社，2005.

[5]华东师范大学版本.数学分析[M].北京：高等教育出版社，2003.

[6]华东师范大学版本.数学分析答案[M].北京：高等教育出版社，2003.

G642.41

A

1674-9324（2014）04-0117-02

尹红然（1982-），女，河北邢台人，硕士，讲师，主要从事张量分析研究。