基于网络服务模式的动态路径规划蚁群算法
夏 英,李芳芳
(重庆邮电大学空间信息系统研究所,重庆 400065)
0 引言
在城市建设和发展的过程中,路网日益复杂且规模不断扩大,城市交通问题日趋严重。智能交通系统(intelligent transportation systems,ITS)实现了道路利用效率最大化,大幅度提高路网的通行能力并改善人们的出行质量。随着智能手机等移动终端设备的日益普及,以及云计算、移动互联网等技术的不断发展,人们对网络环境下的动态路径规划服务提出了需求。网络服务模式下的路径规划服务中心根据用户发出的导航请求,在服务器端进行最优路径规划操作,并通过无线网络将导航信息实时发布给用户。与传统的导航相比,网络服务模式下的路径规划无需手持终端存储导航地图等数据,也无需进行复杂的计算。网络环境下的动态路径规划服务需要结合实时交通数据,同时支持多用户访问,这对传统的面向个人用户的路径规划方法提出了挑战。
蚁群算法是一种模拟进化算法[1],具有分布式计算、信息正反馈和启发式搜索等特征,易于与其他方法相结合,在组合优化方面得到了广泛的应用。传统的蚁群算法存在易早熟、陷入局部最优解等问题。针对这些问题,国内外学者们对蚁群算法提出了多种改进。例如,德国学者Stutzle T等[2]提出“最大最小蚂蚁系统”(MAX-MIN ant system,MMAS),通过限制路径上的信息素来克服停滞问题,并通过调整每一代中最好的蚂蚁个体所走的路径上的信息来加快收敛速度。吴庆洪等[3]从遗传算法中得到启发,在蚁群算法中采用了逆转变异机制。徐精明等[4]对蚁群进行分工,提出了一种多态蚁群算法。在蚁群算法基础上的改进还包括基于信息素扩散的蚁群算法[5],基于GPU的共享信息素矩阵多蚁群算法[6]等。
这些算法应用到路径规划问题中时,大多只是针对单个用户需求,很少考虑多用户同时请求服务时如何共享资源、提高计算效率。考虑到网络服务模式下的路径规划服务是面向多用户的,本文在多态蚁群算法的基础上,提出一种多用户共享信息素的两阶段蚁群算法,以此提高网络模式下的路径规划效率。
1 相关研究
1.1 蚁群算法基本原理
自然界中的蚂蚁,能找到食物源到巢穴间的最短路径,依靠的是其自身分泌的一种具有挥发性的物质(信息素)[7]。蚂蚁在走过的路径上留下信息素,并能识别信息素且有向其浓度高的方向前进的特性。在食物源和蚁巢之间,假设所有蚂蚁的速度一样(如图1所示),在相同的时间内蚂蚁走过较短路径的次数较多,释放的信息素相对来说也较多,更多蚂蚁选择较短路径的可能性也较大,路径上的信息素进而也就更多。在这种正反馈机制下,从蚁巢到食物源的最短路径被逐渐的选择出来,如图2所示。

图1 蚂蚁在有障碍物情形下的运动状态Fig.1 Ants’motion state in case of obstacle
以求解旅行商问题(traveling salesman problem,TSP)为例来叙述基本的蚁群算法模型。

图2 蚂蚁最终选择的路径Fig.2 Final route ants choose

道路上的信息素随着时间的推移会有一定量的挥发,假设所有蚂蚁经过n个时刻完成了一次循环,各路径上的信息素量根据(2)式做调整。

(2)式和(3)式中:参数ρ表示信息素的残留程度;Δτij表示本次循环中路径(i,j)上的信息量的增量;表示第k只蚂蚁在本次循环中留在路径(i,j)上的信息量。
1.2 网络服务模式下的动态导航
在网络服务模式下的动态路径规划服务中,由服务中心通过统一的数据接口接入、存储多源异构交通数据,并通过数据融合技术对接入的实时路况交通数据进行处理,从而获取城市路网的真实交通流状态参数信息;服务中心作为信息的存储、处理中枢,根据用户发出的导航请求,进行最优路径规划操作,并通过无线网络将导航信息实时发布给用户。用户只需有一个能够接入网络的手持终端即可请求该服务。随着云计算、物联网等技术的快速发展,网络服务模式下的动态导航成为可能。
2 基于网络服务模式的动态路径规划算法
2.1 多态蚁群算法的思想
多态蚁群算法[4]是徐精明等在基本蚁群算法的基础上,按照蚂蚁分工不同,把蚁群分成侦察蚁群和搜索蚁群。每种蚁群分泌不同的信息素,侦察蚁群的任务是每个侦察蚁以当前所在的节点为中心对周围近邻节点做局部侦察,并用侦察素来记录侦察结果,为搜索蚁到该节点在选择下个节点的时候提供辅助信息;搜索蚁群的任务是做全局搜索,每到一个节点,根据侦察蚁侦察出来的结果,来选择下一个节点,直到达到目的地。多态蚁群算法将局部侦察与全局搜索相结合,缩小搜索范围从而提高算法的收敛速度。

在规模为n个节点的路网中,将n个侦察蚁分别放在n个节点上,每个侦察蚁以所在节点为中心,侦察其他n-1个节点,S为一个 n×n矩阵,S[i][j]元素用于存放第i个侦察蚁侦得到的节点i到节点j个节点的侦察结果。(4)式中表示以i为中心,到其他n-1个节点的最小距离;dij为i到j的实际距离;MAXPC是对不同路网规模下最大可选节点所作的一个统计值[8]。在蚂蚁选择下个要走的节点时,对路网中每个节点而言,都从离它最近的MAXPC个节点中选择一个节点做为近邻节点,而不是从剩下的所有节点中任意选择一个,这样将原来的解空间由n!减小到nMAXPC,加快寻优速度[9]。
根据侦察结果,对初始时刻路网中各条路径上的信息素量τij(0)赋值。
(5)式中:C为一个常数 为i到其他n-1个节点的最大距离。搜索蚁群在搜索过程中,搜索蚁每到一个节点,结合侦察素,只需在较小范围内搜索,大大减小了搜索范围。

2.2 两阶段蚁群算法
针对网络服务模式下的动态路径规划是面向多用户这一特点,在多态蚁群算法基础上提出一种多用户共享信息素的路径规划算法—两阶段蚁群算法。该算法主要包括侦察阶段和搜索阶段,用户可以共享侦察阶段得到的道路信息素,减小了服务器的计算量。
在侦察阶段融入动态交通信息,侦察蚁群侦察道路上的交通状况,结合当前道路的饱和度信息,用当前道路上的平均车速v来表示,并用侦察素来记录侦察结果,根据侦察结果初始化道路信息素。为防止某些道路上的信息素过大或者过小,导致算法易陷入局部最优收敛,把道路上的信息素范围限制在[ζmin,ζmax]。该阶段初始化的路网信息素矩阵可以供在同一路网上的多个用户在搜索阶段共同使用。
侦察阶段算法描述如下。

为加快算法收敛速度,受细菌觅食算法[10]启发,引入优胜劣汰机制。在搜索蚁群搜索最优路径过程中,设置蚂蚁在单个搜索过程中所允许走过的最大步长STEPmax,当蚂蚁在一次搜索过程中,走过的步长大于STEPmax仍没有到达目标节点,则被淘汰;为维持搜索蚁群数量,当所有搜索蚂蚁完成一次搜索后,恢复搜索蚁群总数量,进入下一轮搜索。这样在一定程度上减少了在蚂蚁陷入局部搜索时的时间开销[11]。
搜索阶段算法描述如下。


从算法时间复杂度的角度来分析,两阶段蚁群算法主要包含侦察阶段和搜索阶段。侦察阶段只与路网节点数和最大可选节点数有关,该阶段的时间复杂度为O(MAXPC×n×n),其中n表示路网节点个数,MAXPC表示路网最大可选节点数;搜索阶段与搜索蚁个数m,最大迭代次数NC,一次循环中每只蚂蚁允许走的最大步长STEPmax,以及最大可选节点数有关,该阶段的复杂度为O(NC×MAXPC×m×STEPmax)。多态蚁群算法的时间复杂度为O(NC×MAXPC×m×n)。通常情况下 STEPmax小于n,两阶段蚁群算法在时间复杂度上优于多态蚁群算法。
3 实验结果及分析
为验证两阶段蚁群算法的有效性以及对网络服务模式的适应性,分别用2组实验与多态蚁群算法进行对比分析。实验环境为 Intel(R)Dual-Core CPU E5300@2.60GHz,2 GByte内存,操作系统为Windows XP。
实验1 对比2个算法的计算效率。
在Matlab平台下做仿真,数据集选取TSPLIB标准库[12]中的数据Eil51,算法运行20次并记录统计结果,对比两阶段蚁群算法与多态蚁群算法在求解TSP问题中的计算效率。统计结果如表1所示。
由表1可以看出,获得最优结果质量相同情况下,两阶段蚁群算法的平均运行时间低于多态蚁群算法。

表1 统计结果分析Tab.1 Statistical results analysis
实验2 验证算法在网络服务模式下的有效性。
为验证两阶段蚁群算法在网络服务模式下的有效性,本文选用上海市路网和交通实际数据。路网包含240个结点和352条路段,使用C#语言在Visual Studio 2010环境下进行实验,模拟多个用户请求导航服务。算法参数设置为:侦察蚁n=240,搜索蚁m=80,信息素挥发因子 ρ=0.3,参数 α=1,β=3,信息素总量Q=100,最大迭代次数NC=200。比较两阶段蚁群算法和多态蚁群算法在求得的最优解质量相同情况下的用户平均执行时间。
表2和表3分别是与实验路网相对应的路段表和结点表。表2中ID表示道路的唯一标识,Fnode和Tnode分表表示路段首尾结点,Length表示路段长度,Name为路段的名称。表3中ID表示结点的唯一标识,Lat和 Lon分别表示该结点的经度和纬度,Link1,Link2,Link3,Link4 分别表示与该结点相关联的结点ID。
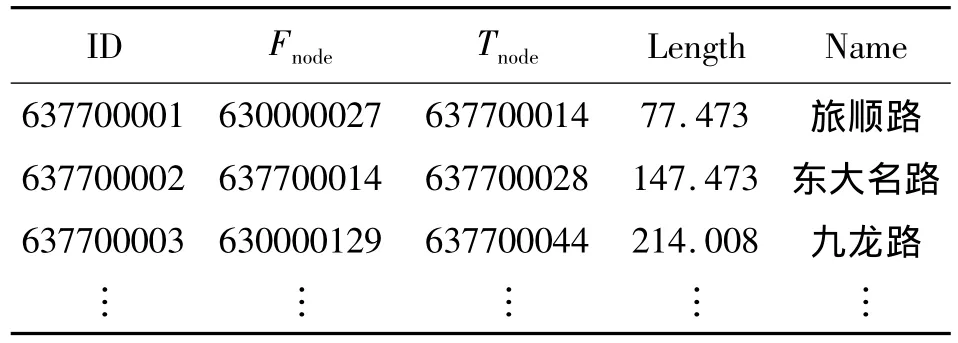
表2 路段表Tab.2 Rode data
实验中道路信息素初始值根据道路长度以及交通流量进行初始化。两阶段蚁群算法在搜索阶段共享了侦察阶段得到初始化信息素,对同一路网上的信息素只用执行一次初始化,而多态蚁群算法在计算最优路径时候,用户数量决定信息素的初始化次数。实验结果如图3所示。

图3 平均执行时间Fig.3 Average execution time
从图3可以看出,在首次为用户计算最短路径的时候,两阶段蚁群算法与多态蚁群算法相比,在搜索效率上有提高,此时是因为两阶段蚁群算法自身在搜索效率上的优势;随着用户数量的增多,两阶段蚁群算法相对多态蚁群算法,在执行效率上的优势明显。这是因为两阶段蚁群算法在其他用户搜索最优路径时,不需要再次进行道路信息素初始化,而多态蚁群算法对每个用户而言仍需要初始化道路信息素。
4 结论
针对网络服务模式下面向多用户的动态路径规划问题,在多态蚁群算法的基础上,提出两阶段蚁群算法。在为用户计算最优路径的时候共享计算资源,减少服务器端负载;在蚂蚁完成一次搜索的过程中,借鉴了细菌觅食算法,引入优胜劣汰机制,提高了算法计算效率。实验表明,两阶段蚁群算法不仅在计算效率上有所提高,且在网络服务模式下表现出明显的优势。
在动态交通状况方面,目前仅仅考虑了动态路网中道路的平均车速以及道路长度这2个因素,下一步研究中将考虑加入用户个人的偏好等因素。
[1]DORIGO M,MANIEZZO V,COLOMIA.The Ant System:Optimization by a colony of cooperating agents[J].IEEE Transactions on Systems,Man and Cybernetics,Part B,1996,26(1):29-41.
[2]STUTZLE T,HOOSHH.MAX-MIN ant system and local search for the traveling salesman problem[C]//In:IEEE Int’l Conf.on Evolutionary Computation.Indianapolis:IEEE Press,1997:309-314.
[3]吴庆洪,张纪会.具有变异特征的蚁群算法[J].计算机研究与发展,1999,36(10):1240-1245.
WU Qinghong,ZHANG Jihui.AN ant colony algorithm with Mutation Features[J].Computer Research and Development,1999,36(10):1240-1245.
[4]徐精明,曹先彬,王煦法.多态蚁群算法[J].中国科学技术大学学报,2005,35(1):59-65.
XU Jingming,CAO Xianbin,WANG Xufa.Polymorphic ant colony algorithm [J].University of Science and Technology of China,2005,35(1):59-65.
[5]黄国锐,曹先彬,王煦法.基于信息素扩散的蚁群算法[J].电子学报,2004,32(5):865-868.
HUANG Guorui,CAO Xianbin,WANG Xufa.An ANT Colony Optimization Algorithm Based on Pheromone Diffusion [J].Chinese Journal of Electronics,2004:32(5)865-868.
[6]白洪涛,欧阳丹彤,李熙铭,等.基于GPU的共享信息素矩阵多蚁群算法[J].吉林大学学报,2011,41(6):1678-1683.
BAI Hongtao,OU YANG Dantong,LI Ximing,et al.Multiple ant colonies sharing common pheromone matrix based on CPU[J].Journal of Jilin University,2011,41(6):1678-1683.
[7]杨清平,邓小清,蒲国林,等.网格资源的组织与发现研究[J].重庆师范大学学报:自然科学版,2008,25(04):70-73.
YANG Qingping,DENG Xiaoqing,PU Guolin,et al.Research into Organization and Discovery of Drid Resource[J].Journal of Chongqing Normal University:Natural Science Edition,2008,25(04):70-73.
[8]全惠云,文高进.求解TSP的子空间遗传算法[J].数学理论与应用,2002,22(1):36-39.
QUAN Huiyun,WEN Gaojin.Subspace genetic algorithm for TSP[J].Mathematical theory and application,2002,22(1):36-39.
[9]张春艳,刘清林,孟珂.基于蚁群优化算法的云计算任务分配[J].计算机应用,2012,32(5):1418-1420.
ZHANG Chunyan,LIU Qinglin,MENG Ke.Task allocation based on ant colony optimization in cloud computing[J].Computer Applications,2012,32(5):1418-1420.
[10]周雅兰.觅食优化算法的研究与应用[J].计算机工程与应用,2010,46(20):16-21.
ZHOU Yalan.Research and application on bacteria foraging optimization algorithm [J].Computer Engineering and Application,2010,46(20):16-21.
[11]黄翰,郝志峰,吴春国,等,蚁群算法的收敛速度分析[J].计算机学报,2007,30(8):1345-1353.
HUANG Han,HAO Zhifeng,WU Chunguo,et al.The Convergence Speed of Ant Colony Optimization [J].Chinese Journal of Computers,2007,30(8):1345-1353.
[12]Universitat Heidelberg.A library of sample instances for the TSP and related problems[EB/OL].(2008-07-26)[2012-04-25].http://www.iwr.uni-heidelberg.de/groups/comopt/software/TSPLIB95/.
(编辑:田海江)

