基于迭代用户选择的合作频谱感知算法
樊陆陆,申 滨,黄 琼
(重庆邮电大学移动通信重点实验室,重庆 400065)
0 前言
随着无线通信业务的迅猛发展,对数据传输速率的要求越来越高,通信系统对无线频谱资源的带宽要求也相应提高,无线通信频谱资源愈来愈显得缺乏。然而,据2002年授权的SPTF(spectrum policy task force)对某些频谱资源的使用情况所做的调查显示,在某一个时间和空间内只有5% ~85%的频谱被占用。对于解决这种一方面是频谱紧缺;另一方面是频谱浪费的矛盾,而认知无线电(cognitive radio,CR)被认为是最佳方案[1]。
频谱感知是CR实现对外部授权频谱状态认知的关键技术和环节。频谱感知技术有3种经典的单节点感知方案,包括:能量检测方案[2]、匹配滤波器检测方案[3-5]、循环平稳检测方案[6-8]。匹配滤波器检测方案需要知道授权用户(primary user,PU)信号的先验知识,而在实际中这一要求是很难满足的。循环平稳检测方案对噪声的不确定性具有很强的鲁棒性,但是系统实现的复杂度高。在无法获得PU信号相关信息的情况下,能量检测(energy detection,ED)方案是最优的检测方法,而且实现简单。但其缺点是要预先知道噪声功率,且感知性能与判决门限密切相关。在实际情况下,噪声功率是很难预先准确获得的。
为了克服单节点检测器在感知性能上的缺陷,近几年出现了基于多个认知用户(secondary user,SU)合作的频谱感知方法:硬判决融合(hard decision fusion,HDF)、数据软融合(soft data fusion,SDF)。早期的合作频谱感知研究集中在对多个SU本地检测的HDF方案设计及相应的性能评估上,主要包括AND,OR和K/N规则。关于HDF的典型研究如文献[9-13],其中,文献[9-10]是最早对 HDF的研究,证明了多用户合作感知有益于提高单用户的频谱感知性能,并可以减轻单个能量检测器的灵敏度设计负担。文献[11]综合研究了HDF方案的最优融合准则和最优阈值设计。文献[12-14]提出了基于用户簇的HDF方案并扩展为基于用户群组架构的合作方法,可以在此基础上构建SDF/HDF混合方案。由于HDF仅需要在参与合作感知的多个SU与融合中心(fusion center,FC)之间传递本地硬判决数据(见图1a),因此,系统开销小,实现简单,最终全局判决延迟较小。然而,单个SU接收到的数据差异性比较大,单独做出的判决可靠性不高,故HDF检测方案还需要进一步改进。
为了进一步提高合作感知的性能,SDF方案得到广泛研究,SDF方案中参与合作频谱感知的各个SU将各自的感知数据直接发送给FC,FC利用接收到的多个不同的随机信号副本生成全局检验统计量(global test statistic,GTS)并进行判决(见图1b)。尽管SDF方案在实现上比HDF方案要复杂,但因其更充分地利用了隐藏在多个频谱监测数据下的信息,因而能够大幅度地提高HDF方案下的感知性能。

图1 认知无线电HDF与SDF频谱感知场景Fig.1 Spectrum sensing scenarios of HDF and SDF in cognitive radio
近年来,学术界提出了利用随机矩阵理论(random matrix theory,RMT)来实现频谱感知的方案。文献[15]提出了最大最小特征值检测 (maximumminimum eigenvalue,MME)方案,采用RMT对多个SU接收信号所组成的采样协方差矩阵的特征值进行分析,利用极限渐进谱理论求出该协方差矩阵最大和最小特征值的极限值,并将这2个极限的比值作为频谱检测的检验统计量,设计出了一种基于RMT的合作频谱感知算法。文献[16]提出了算术几何平均(arithmetic to geometric mean,AGM)和信号特征值子空间(signal-subspace eigenvalue,SSE)频谱感知方案,这2种方案不需要任何的PU信息和信道信息,仅利用多天线接收到信号的样本协方差矩阵。具体地,AGM无需知道任何先验信息;SSE只需知道噪声功率。当PU信号是相关信号时,SSE的性能要优于ED,而ED的性能要优于AGM。在同样已知噪声功率的情况下,SSE优于ED是因为所要检测的PU信号是相关信号,然而,ED在检测独立同分布(independent identically distributed,IID)信号时性能最优。文献[17]提出了一种最优合并能量检测(optimally combined energy detection,OCED)算法,OCED预先知道PU信号的短方差矩阵,仿真性能要优于MED和ED。文献[18]提出了一种最大特征值检测 (maximum eigenvalue detection,MED)方案,该方案克服了文献[15]中判决门限固定不变的缺点,提高了感知性能,但是,MED同样存在需预知噪声功率的缺陷。文献[19-20]根据RMT提出了一种新的基于最大特征值-能量检测(maximum eigenvalue-energy detection,ME-ED)的合作感知方案,该算法将SU接收信号样本协方差矩阵的最大特征值与接收信号平均能量的比值作为判决统计量。ME-ED方案无需预知PU信号的任何先验信息及噪声功率,与MED和ED相比,该方案不仅对噪声的不确定性不敏感,而且在噪声存在波动的情况下,其感知性能最优,鲁棒性最强。表1给出了上述各种方案的性能对比。

表1 不同方案性能对比Tab.1 Performance comparison of different algorithms
本文提出了一种基于迭代用户选择(iterative users selection,IUS)的合作频谱感知算法。该算法根据参加合作感知全部用户的频谱观测数据,以迭代方式逐个选出部分用户,并仅在此部分用户所提供的最有代表性的接收数据基础上,进行数据加权合并,以产生最后的全局检验统计量。仿真结果显示,当PU信号是IDD信号时,IUS的检测性能与SSE相当,且优于MED和ED;当PU信号是相关信号时,IUS的检测性能与 SSE,MED相当,且优于ED。IUS算法无需任何先验信息,摒弃了错误或冗余的噪声数据,达到了较好的感知性能,可作为现实中合作频谱感知的具体实现方案。
1 信号模型
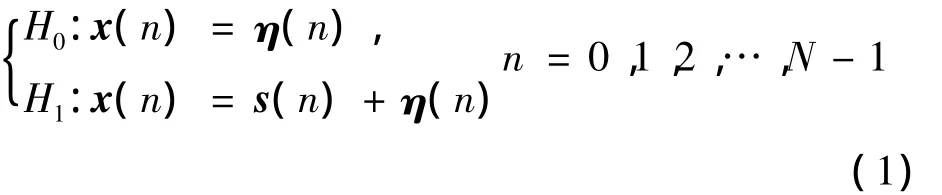
假设每一个认知节点在每次频谱感知时间内的采样次数为N,则认知网络中参与合作感知的M个认知节点对各自的接收信号采样得到的信号样本构成一个样本矩阵X=[x(0)]x(1) … x(N-1)],其中,x(n)=[x1(n)x2(n) … xM(n)]T,X是一个M×N的矩阵。认知节点对PU信号的检测是一个二元假设检验问题:(1)式中:H0假设认知节点接收信号中只存在噪声;H1假设认知节点接收信号中既存在噪声又存在PU信号;η(n)=[η1(n) η2(n) … ηM(n)]T是CR接收端的加性高斯白噪声矢量,其均值为0、协方差矩阵为σ2I,其中,σ2为噪声功率,I为M阶单位矩阵;s(n)为接收端接收到的PU信号,其均值为0、协方差矩阵 Rs=E[s(n)sH(n)],其中,(·)H表示矩阵转置,E[·]表示期望。x(n)的协方差矩阵也可以表示成Rx=E[x(n)xH(n)]。我们可以计算x(n)的协方差矩阵为
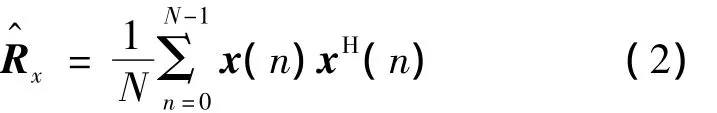
2 迭代用户选择算法

3 )在实际中,由于Rs极难预先获知,故针对1)和2)中M'的判决非常困难,所以,需要找到一种机制来确定M'。针对这个情况,我们提出了IUS算法,预期实现尽可能精确地确定rank(Rs)所对应的合作用户子集的目标。
3 IUS算法流程
在传统的合作频谱感知技术中,融合中心在获取到所有参与频谱感知的合作用户上报的频谱观测数据之后,直接根据各种算法机制生成GTS。IUS算法流程与传统的合作感知流程的区别在于:数据融合中心在生成GTS之前,是否对全部合作用户上报的数据进行筛选和处理。具体地,IUS将根据信号样本协方差矩阵的特征值确定加权的大小,并且给对应特征值大的合作用户分配较大的权重,给对应特征值较小的合作用户分配较小的权重,于是就形成了基于迭代用户选择的特征值加权算法。图2给出了IUS的算法流程及后面给出了IUS算法执行步骤。

图2 IUS算法流程图Fig.2 IUS flow chart

步骤2 假设当前迭代次数为p(p≥1),其对应的第p次用户选择判决门限随迭代次数变化的表达式为

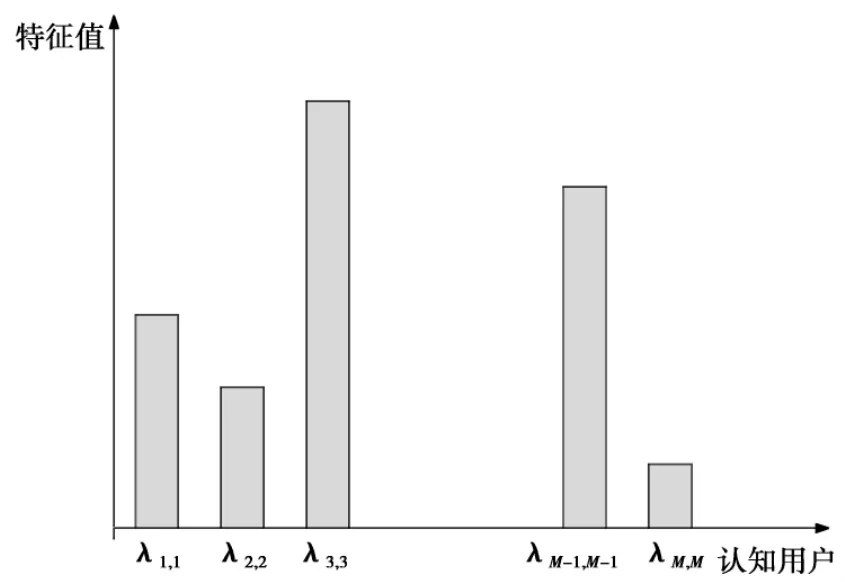
图3 原始特征值分布图Fig.3 Distribution map of the original eigenvalue
步骤4 若任意的wi非负,即得到最优的权重向量 w=[w1,…,wM'],用户选择门限值为 εp;则IUS的GTS可以表示为
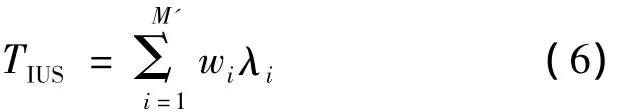
数据融合中心在生成GTS之前,虽然IUS对全部合作用户上报的数据进行筛选和处理,摒弃了无效的检测数据,但是仍然需要所有的SU收集频谱观测数据,再在此基础上进行用户选择,因此,并未真正节省SU数据上报的开销。

图4 排序后的特征值倒数分布图Fig.4 Distribution map inverse of the eigenvalue after ordering
IUS是在传统的合作感知中加入“迭代用户选择”这一操作步骤,因此,严格意义上,对感知时间长度极度严格限制的CR系统来说,会引入一定的延迟。但是考虑到实际中用户数总量并不会太大,因而,该部分由IUS引入的操作时延仍是可忽略的或可控的。
4 仿真及分析
图5和图7表示当PU信号为IID信号和相关信号时检测概率随信噪比变化的情况。当相关系数rh0=0时,PU信号的协方差矩阵中非对角线上的数据为0,此时PU信号是IID信号;当0<rh0<1时,PU信号的协方差矩阵中非对角线上的数据为非0,此时PU信号是相关信号。图6和图8是相对应的虚警检测概率仿真图;图9表示本文所提出的IUS在不同相关系数下的性能对比。仿真参数设置为认知节点数M=10,时间样本点数N=1 000,仿真次数为5 000次,期望虚警概率设置为PFA=0.1。
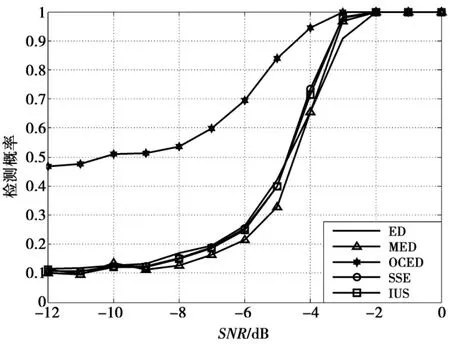
图5 IID信号下的性能对比Fig.5 Performance comparison of IID signal

图6 IID信号下的虚警检测概率对比Fig.6 False alarm detection probability comparison of IID signal

图7 相关信号下的检测性能对比Fig.7 Performance comparison of correlation signal
从图6和图8中可以看出,不论是IID信号还是相关信号,各种方案的虚警概率都较好的保持在期望虚警概率附近。从图5和图7中可以看出,在IID信号和相关信号下,性能最好的算法是OCED,这是因为该算法是用最大特征向量进行加权,预先知道信号的协方差矩阵Rs,而在现实中这是很难做到的;SSE通过样本信号功率与噪声功率的比较得到有效的信号子集,即信号子空间,但是必须预先知道噪声功率;而本文提出的基于IUS的合作频谱感知算法不需要任何的先验信息,直接对样本检测信号进行处理。仿真结果显示,在IID信号和相关信号下,IUS与SSE性能几乎一样;同时本文提出的基于IUS的合作频谱感知算法在相关信号下明显优于传统的ED算法;MED在检测相关信号时性能较好,检测IID信号时性能较ED要差很多,这是因为ED能更好地捕捉IID信号。
图9表示IUS在不同的相关系数下的性能对比,从图9中可以看出,随着相关系数rho增大,检测性能越来越好。

图8 相关信号下虚警检测概率对比Fig.8 False alarm detection probability comparison of correlation signal

图9 不同相关系数下的用户选择检测性能对比Fig.9 Performance comparison of different correlation coefficient
5 结束语
本文在合作频谱感知基础上提出了一种基于IUS的新合作频谱感知算法,此算法无需任何先验信息,通过用户选择算法筛选出更能代表整体的特征数据,摒弃了错误或冗余数据,达到了较好的感知性能,可作为现实中合作频谱感知的具体实现方案。
[1]WU Suwen,ZHU Jinkang,QIU Ling,et al.SNR-based weighted cooperative spectrum sensing in cognitive radio networks[J].Journal of China Universities of Posts and Telecommunications,2010,17(2):1-7.
[2]RAHUL T,ANANT S.Fundamental limits on detection in low SNR under noise uncertainty[C]//IEEE.International Conference on Communications and Mobile Computing.Maui:IEEE Press,2005:13-16.
[3]SAHAIA,CABRIC D.Spectrum sensing:Fundamental limits and practical challenges[C]//IEEE.IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks(DYSPAN).Baltimore:IEEE Press,2005.
[4]CHEN H S,GAOW,DAUTD G.Signature based spectrum sensing algorithms for IEEE 802.22 WRAN[C]//IEEE.Int.Conf.Communication(ICC).Glasgow:IEEE Press,2007:6487-6492.
[5]CABRICD,TKACHENKO A,BRODERSEN RW.Spectrum sensingmeasurements of pilot,energy,and collaborative detection[C]//IEEE.Military Communication.Conf.(MILCOM).Washington:IEEE Press,2006:1-7.
[6]GARDNERW A.Exploitation of spectral redundancy in cyclostationary signals[J].Signal Processing Magazine,IEEE,1991,8(2):14-36.
[7]漆渊,彭涛,钱荣荣,等.认知无线电中基于循环平稳特征的频谱感知方法[J].重庆邮电大学学报:自然科学版,2009,21(3):353-357.
QIYuan,PENG Tao,QIAN Rongrong,et al.Cyclostationarity-based spectrum sensing in cognitive radio[J].Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition,2009,21(3):353-357.
[8]赵宏强.频谱细化算法分析[J].四川兵工学报,2013(5):105-109.
ZHAO Hongqing.Analysis of Spectrum Zoom Algrithms[J].Journal of Sichuan Ordnance,2013(5):105-109.
[9]GHASEMIA,SOUSA E S.Impact of user collaboration on the performance of sensing based opportunistic spectrum access[C]//IEEE.Vehicular Technology Conference.Montreal,Que:IEEE Press,2006:1-6.
[10]MISHRA SM,SAHAIA,BRODERSEN RW.Cooperative sensing among cognitive radios[C]//IEEE.International Conference on Communications(ICC 2006).Istanbul:IEEE Press,2006:1658-1663.
[11]ZHANGWei,MALLIK R K,KHALED Letaief.Cooperative spectrum sensing optimization in cognitive radio networks[C]//IEEE.International Conference on Communications(ICC 2008).Beijing:IEEE Press,2008:3411-3415.
[12]SUN Chunhua,ZHANGWei,BEN K.Cluster-based cooperative spectrum sensing in cognitive radio systems[C]//IEEE.International Conference on Communications(ICC 2007).Glasgow:IEEE Press,2007,2511-2515.
[13]SUN Chunhua,ZHANGWei,KHALED Letaief.Cooperative spectrum sensing for cognitive radios under bandwidth constraints[C]//IEEE.Wireless Communications and Networking Conference.Kowloon:IEEE Press,2007:1-5.
[14]ZHU Jiang,XU Zhengguang,WANG Furong.Double threshold energy detection of cooperative spectrum sensing in cognitive radio[C]//IEEE.Cognitive Radio Oriented Wireless Networks and Communications. Singapore:IEEE Press,2008:1-5.
[15]CARDOSO L S,DEBBAH M,BIANCHIP,et al.Cooperative spectrum sensing using random matrix theory[C]//IEEE.International Symposium on Wireless Pervasive Computing.Santorini:IEEE Press,2008:334-338
[16]ZHANG Rui,LIM T,LIANG Yingchang,et al.Multiantenna based spectrum sensing for cognitive radios:A GLRT approach [J].Communications,IEEE Transactions on,2010,58(1):84-88.
[17]ZENG Yonghong,LIANG Yingchang,ZHANG Rui.Blindly combined energy detection for spectrum sensing in cognitive radio [J].Signal Processing Letters,IEEE,2008,15:649-652.
[18]ZENG Yonghong,KOH Chooleng,LIANG Yingchang.Maximum eigenvalue detection:theory and application[C]//IEEE.International Conference on Communications.Beijing:IEEE Press,2008:4160-4164.
[19]曹开田,杨震.一种新型的基于最大特征值的合作频谱感知算法[J].电子与信息学报,2011,33(6):1367-1372.
CAO Kaitian,YANG Zhen.A novel cooperative spectrum sensing algorithm based on themaximum eigenvalue[J].Journal of Electronics& Information Technology 2011,33(6):1367-1372.
[20]ZENG Yonghong,LIANG Yingchang.Eigenvalue-based spectrum sensing algorithms for cognitive radio[J].Communications,IEEE Transactions on,2009,57(6):1784-1793.
(编辑:魏琴芳)

