一种新的TDCS 基函数随机相位产生方法及性能分析
王 舒,达新宇,褚振勇,谢铁城,邹 维
(空军工程大学信息与导航学院,陕西西安 710077)
0 引言
变换域通信系统(transform domain communication system,TDCS)[1]是一种具有独特抗干扰性能的通信方式,特别适合于频谱拥挤、频段共用、军事领域等环境下的应用。TDCS通过对发送信号进行信号设计、从信号构成中消除干扰频谱、彻底解决干扰信号对传输信号影响的方式,提高系统的抗干扰性能,是一种与传统通信系统抗干扰原理完全不同的抗干扰通信系统[2-6]。
目前,对TDCS的主要研究集中于变换域内信号波形的设计,这里的变换域是指使用各种变换域技术剔除干扰,生成基函数的幅度谱[4-6],同时,由于采用伪随机(pseudo random,PR)序列用以生成基函数的伪随机相位向量,使得TDCS信号具有自正交性,因此,呈现出低截获性能。TDCS的伪随机相位通常是由一个最长二进制伪随机序列(M序列)产生的,但是,M序列但其互相关特性并不理想,正交性不强,导致其可用数目不多,系统容量有限,影响了系统的多址应用。针对M序列伪随机相位生成法的不足,文献[7]提出了采用双M序列控制基函数相位映射的方法,增强了基函数的随机性;文献[8-9]中基函数伪随机相位均采用Logistic混沌序列来实现,并从相关特性,平衡性及游程特性等方面分别比较了基函数采用M序列与Logistic混沌序列的优缺点,研究结果表明,采用Logistic混沌序列可产生数量巨大且互相关性更弱的基函数,相较于M序列具有更好的伪随机特性与多址特性。
1 基函数的生成
在TDCS中,基函数决定发射信号波形及系统抗干扰性能,对系统具有十分重要的作用。经过对环境采样、门限判决、相位映射等处理,得到频谱与干扰谱正交的基函数[10]

(1)式中:B(u)的幅值A(u)(即空闲频谱标记矢量)经过环境谱估计和门限判决产生,其元素为1或0,分别表示频段可用或者不可用;B(u)的相位谱φ(u)通过伪随机相位生成器获得,该矢量相位服从[0,2π]均匀随机分布且与频谱标记向量长度相同。根据发射功率要求作出一定的幅度调整(调整比例为C),对其作反傅里叶变换(inverse discrete fouriertransform,IDFT)后得到了调制所用基函数的时域波形,利用基函数进行数据调制,最后经功放、天线输出。
1.1 传统伪随机相位生成方法
对于空闲频谱标记矢量长度为N的基函数,其对应匹配的伪随机相位向量的第k个元素表示为exp(j2πmk/N),k=0,1,…,N -1。其中,mk是由一个lb N级线性反馈移位寄存器(linear feedback shift register,LFSR)生成的伪随机整数,mk∈{0,1,…,N-1}。图1给出了伪随机相位生成的原理框图。

图1 传统伪随机相位生成原理框图Fig.1 Principle block diagram of traditional pseudorandom phase generation
伪随机相位的生成过程如下:
1 )由一个lb N阶LFSR来产生M序列,这个伪随机序列的周期是N-1。
2 )在这个M序列中取r个数,作为相位映射器的输入。这r个数可以包括lb N阶LFSR输出的任意组合,但是为了便于分析与描述取连续的r个数。r决定了2r个可能的相位。

4 )LFSR偏移s个状态后,按同样方法再取r个数,再经过相位映射器得到下一个随机相位。

1.2 采用双混沌序列法产生随机相位
本文采用混沌序列来构成随机相位映射器。混沌序列具有类白噪声性,同时具有理想的相关特性,另外,利用初值可以精确地重构混沌序列,这些优良特性非常适用TDCS。本文采用一种常用的混沌映射——Chebyshev 映射[11],其形式为

由(2)式可以看出,混沌序列完全依赖于初始值x0,一旦初始值改变,其产生的混沌序列也将完全不同。因此,在TDCS的多址应用中,可以将由不同初值产生得到的混沌序列(作为多址接入的地址码)分配给不同的用户。
利用双混沌序列法生成伪随机相位的过程如下。
1 )采用等间隔的方式来生成初值序列。同时,由于混沌序列中的相位映射长度2ri等于基函数采样点数N,即2ri=N。而理论上混沌序列的长度可以是无限长的,需将产生的混沌序列截短,并依次移位进一个lb N级移位寄存器,即就是混沌序列 1;
2 )在生成的混沌序列1中选取lb N级移位寄存器中的ri个抽头构成随机相位映射器。
通过上述混沌映射法,以期提高基函数相位谱的相关性。同时由上述分析发现,基函数相位的随机性主要与相位映射器的抽头ri的位置有关。ri一经确定,则在一个周期内,单位圆上的随机相位总数就不再发生变化。而基函数的随机性直接由相位的随机性决定。
3 )通过将相位映射器的输入ri随机化(利用混沌序列2确定的ri级映射抽头来控制混沌序列1),进一步提高基函数的随机性。混沌序列2的前m级移位寄存器的值决定了ri级映射抽头。如图2所示,混沌序列2的前m个移位寄存器的值ri=4,表示混沌序列有4级映射抽头,抽头对应混沌序列1的前ri(即4)个移位寄存器的值决定了混沌映射的可选相位数量为16(2ri=16)。

图2 ri个相位映射方法Fig.2 Mappingmethod of ri phases
4 ),5)步骤同传统伪随机相位生成方法。
综上所述,对TDCS传统相位映射方案的改进如图3所示。图3中,m为产生混沌序列2的移位寄存器的级数。

图3 利用双混沌序列法产生伪随机相位的原理框图Fig.3 Principle block diagram of using double chaos-sequences to generate the pseudorandom phases
2 基函数的性能分析
2.1 基函数的相关性
TDCS是利用基函数类噪声具有的自正交性进行正交调制,一方面,要求基函数具有良好的自相关性,其主瓣尖锐,而旁瓣很小;另一方面,要求不同基函数的互相关值越小越好,以减小多址干扰。
因此,有必要比较M序列和混沌序列相关性的优劣。为了更为直观地看出比较结果,将M序列和混沌序列按照产生的序列数量以及最大互相关值依次列出,如表1所示。
由于混沌序列的初始敏感性,其序列数量众多,但考虑到实际应用的需求,需对其进行优选,表1所示混沌序列数量为经过优选后的结果。由表1可以看出,当序列长度相同时,混沌序列的数量远远大于M序列的数量,如,当n=9时,M序列的数量仅为48,但混沌序列的数量为276 420,同时,M序列的最大互相关值为113,而混沌序列为31。

表1 M序列和混沌序列产生的序列数量及最大互相关值Tab.1 Sequence number and themaximum mutual-correlation value of M sequence and chaos sequence
在灵活性上,M序列的周期是限定的,而且数量较少,而混沌序列周期是任意的,且数量极大。
在复杂性上,M序列的线性复杂度为移位寄存器的级数,而混沌序列的线性复杂度为N/2,远大于M序列。
2.2 基函数的随机性
基函数矢量的频域数学表达式B(u)为幅度谱矢量A(u)与相位矢量ejφ(u)的乘积,其中,相位矢量是伪随机相位,产生的基函数与噪声的相似程度也由伪随机序列决定,因此,改变基函数使用的伪随机序列可优化其随机性。
图3中,本文方法的基函数相位的每一个伪随机序列的产生是由控制参数m以及映射抽头ri共同决定,即由混沌序列1的N次相位映射以及混沌序列2的当前值共同决定的,对比传统一维M序列生成法,增加了随机映射级数抽头,提高了检测概率。表1中,在线性移位寄存器级数相同的情况下,混沌序列数量远大于M序列数量,由此,混沌序列2生成的随机序列数量增加,对应得到的控制参数ri随机变化范围也相应增大,基函数的随机性进一步提高。
3 仿真结果
图4为N=512,m=7,ri=6时,利用混沌序列映射M序列控制法生成的基函数时域波形,可见其具有良好的类噪声性。图5为利用混沌序列映射M序列控制法生成的基函数时域波形的自相关函数。由图5可以看出,基函数的自相关函数具有类似噪声自相关函数的脉冲形状,自相关峰尖锐,旁瓣很小,基函数的自相关性良好。

图4 双混沌序列法生成的基函数时域波形Fig.4 Time domain waveform of the basis function using double chaos-sequences in phasemapping
在加性高斯白噪声(additive white Gaussian noise,AWGN)信道下,TDCS系统二进制码移键控(binary code shift keying,BCSK)调制传输误比特率为M进制码移键控(code shift keying,CSK)调制的误比特率的近似值为
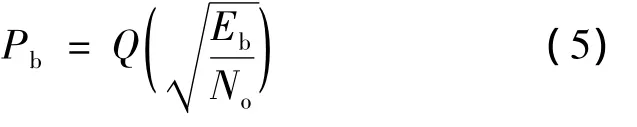

为了评估经过改进后的TDCS的误比特率性能,对于CSK调制的TDCS系统,假设全部频谱可用,即空闲频谱标记矢量元素为全 1;采用加性高斯白噪声信道模型;传统方案采用n=9级的M序列,映射级数ri= 3;对于随机相位映射改进后的方案采用n=9级的混沌序列,映射级数ri∈[1,9]。图6给出了采用CSK调制TDCS系统误比特率随信噪比(signal-to-noise ratio,SNR)变化的仿真曲线图。

图5 双混沌序列法生成的基函数自相关函数Fig.5 Self-correlation function of the basis function using double chaos-sequences in phasemapping
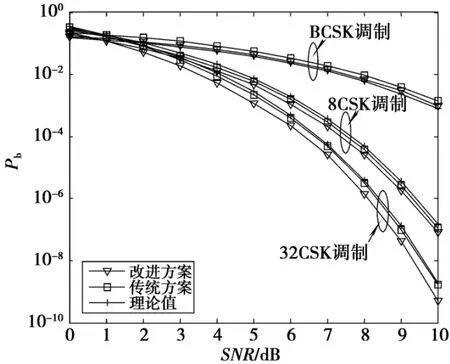
图6 单用户情况下改进前后TDCS系统误比特性能比较Fig.6 Comparison of error performance in TDCS with single user
由图6可以看到,优化后的BCSK调制相对于传统方法误比特性能增益改善了约0.29 dB,更加接近于理论值,因而表明优化后的不同BCSK符号之间的互相关性更弱,这与分析结果相一致。
由图6还可以看到,优化后的TDCS系统采用8CSK及32CSK调制与改进前相比,系统误比特率分别改善了0.32 dB和0.44 dB,这也表明改进后CSK信号相位的随机性增强,同时其相关性得到了改善,即不同序列之间的互相关值更小,与理论分析吻合。同时也发现其理论误比特率高于仿真误比特率,这是因为,由(6)式可看出,多元CSK调制误比特率理论值是实际误比特率的上界值,因此,这一点与理论分析也相一致。
TDCS多址能力是靠伪随机序列映射随机相位来实现的,即通过给用户分不同的伪随机序列码达到区分用户的目的。为了分析TDCS的多址性能,下面将给出多用户下系统误比特率。

(7)式中,Rvu(0)表示不同用户间的互相关值。由(7)式可见,多用户情况下的系统误比特率与系统信噪比以及不同用户间的互相关值有关,且与其成反比。
图7给出了不同数量多用户情况下的系统误比特率,仿真方案中,采用BCSK调制,假设全部频谱可用,即空闲频谱标记矢量元素为全 1;信道模型为AWGN信道;信噪比为0~10 dB;传统方案采用n=9级的M序列;随机相位映射器:ri=3。对于随机相位映射改进后的方案采用n=9级的混沌序列;随机相位映射器:ri∈[1,9]。
从图7中可以看出,TDCS误比特率随着用户数的增加而增加,这是因为各个用户的基函数并不是严格正交的,其互相关值只是趋近于0。而在相同信噪比下,采用改进伪随机相位生成方案比传统方案的系统误比特率要低,这与理论推导相一致。因为改进方案使得基函数伪随机相位的随机性更强,基函数互相关性更弱,用户之间的基函数的干扰就会减小。且通过仿真发现,随着用户数的增加,改进方案的效果更明显,那是因为用户数不断累加,所得的总互相关值减少量也会随之增加,相较于相同用户数的传统方案误比特率会下降得更快。
4 结论
本文基于TDCS提出了一种采用双混沌序列生成基函数伪随机相位的方法,该方法采用各项性能更优的混沌序列,通过增加伪随机相位映射的控制参数,提高了其产生基函数的相关性和随机性。仿真结果证实了本文所提的优化方案相比于传统的伪随机相位生成法,能够获得一定的误比特性能增益,同时呈现出良好的多址性能。
[1]GERMAN E H.Transform Domain Signal Processing Study Final Report[R].Reisterstown,MD:Contract Air Force F30602-86-C-0133,1988.
[2]RADCLIFFERodney A.Design and Simulation ofa Transform Domain Communication System[D].Wright-Patterson AFBOH:Air Force Institute of Technology,1996.
[3]HAN Chuan,WANG Jun,YANG Yaling,et al.Addressing the control channel design problem:OFDM-based transform domain communication system in cognitive radio[J].Computer Networks,2008,52(10):795-815.
[4]曾武,达新宇,申勇,等.基于多级门限判决的TDCS基函数生成及性能分析[J].重庆邮电大学学报:自然科学版,2012,24(3):354-357.
ZENGWu,DA Xinyu,SHEN Yong,etal.A basis function generationmethod of TDCS based on multi-threshold and its performance analysis[J].Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition,2012,24(3):354-357.
[5]WANG Chuandan,ZHANG Zhongpei,LIShaoqian.Interference Mitigating Based on Fractional Fourier Transform in Transform Domain Communication System[J].Journal of Electronics(China),2007,24(2):181-186.
[6]芮国胜,苗俊,杨霄.变换域通信系统的分形门限研究[J]. 系统仿真学报,2009,21(13):4077-4083.
RUIGuosheng,MIAO Jun,YANG Xiao.Research on fractal threshold for TDCS[J].Journal of System Simulation,2009,21(13):4077-4083.
[7]MARSHALL E.Hardeware Realization of a Transform Domain Communication System[D].Wright-Patterson AFB OH:Air Force Institute of Technology,2007.
[8]王传丹,张忠培,李少谦.一种新的基函数产生方法与性能分析[J].电子科技大学学报,2006,35(4):648-652.
WANG Chuandan,ZHANG Zhongpei,LI Shaoqian.A new method of basis function generation in TDCS and its performance analysis[J].Journal of University of Electronic Science and Technology of China,2006,35(4):648-652.
[9]何世彪,季烨,潘辉.TDCS中随机相位的混沌产生方法[J].重庆大学学报:自然科学版,2008,35(12):1381-1385.
HE Shibiao,JI Ye,PAN Hui.A method to generate pseudorandom phase in transform domain communication system by chaosmapping[J].Journal of Chongqing University:Natural Science Edition,2008,35(12):1381-1385.
[10]吕军慰,陈自力,倪蕾.基于数字混沌序列的变换域通信系统基函数产生方法[J].军械工程学院学报,2010,22(5):44-47.
LV Junwei,CHEN Zili,NILei.Amethod to generate basis function in transform domain communication system based on digital chaoticmapping[J].Journal of Ordnance Engineering Collage,2010,22(5):44-47.
[11]ROBERTSM L,TEMPLE M A,MILLSR F,et al.Interference suppression characterization for spectrally modulated,spectrally encoded signals[J].IEEE Electronic Letters,2006,42(19):1103-1104.
[12]李辉.混沌数字通信[M].北京:清华大学出版社,2006.
LI Hui.Chaotic Digital Communication[M].Beijing:Tsinghua University Press,2006.
(编辑:刘 勇)

