一种降低OFDM系统峰均比的循环反馈SLM方法
李英善,段燕辉,王 猛,夏俊丽
(南开大学电子信息与光学工程学院,天津 300071)
0 引言
正交频分复用(orthogonal frequency division multiplexing,OFDM)可对抗无线信道的多径衰落,具有高数据传输率、高频带利用率,被认为是未来无线通信系统的关键技术之一。在OFDM系统中,高速串行的数据流经过串并变换转换为低速并行的若干路子数据流,每个支路的数据速率降低,周期展宽加上循环前缀可有效地消除符号间干扰(inter symbol interference,ISI)的影响。
然而,OFDM符号是若干支路数据的叠加,若各支路在同一相位上叠加会带来幅值的叠加,从而产生大的峰均比(peak to average power ratio,PAPR)。在发送端,大的峰值就要求非线性器件(如,大功率放大器(high-power amplifier,HPA),数/模转换器(D/A))具有较大的线性动态范围。反过来,若大的峰值信号落在非线性器件的非线性区域,会带来非线性失真和带外频谱泄露从而降低系统性能。
通常,降低PAPR的方法大致有3类:限幅类、编码类和概率类。迄今为止,关于PAPR的研究有很多。文献[1]采用了限幅滤波法。限幅滤波是最直接、最简单的方法,但是该方法在限制信号峰值的同时也会带来带内失真和带外频谱泄露,滤波器可消除带外频谱泄露却不能消除带内干扰。文献[2]采用了编码类方法之一的block coding方法。编码类方法并不会给OFDM信号带来干扰。通常可以采用格雷互补码,reed-muller码,M序列等。但是该方法的编码率和带宽效率很低,而且当子载波数增加(>16)时,很难找到合适的码组。选择性映射(selected mapping,SLM)和部分传输序列(partial transmit sequence,PTS)方法属于概率类,该方法可有效地降低峰均比而不带来任何干扰。但是边带信息需占用一定带宽传送至接收机。文献[3]提出了一种用滑动窗搜索辅助信息的次最优PTS方法,很好地降低了PAPR。文献[4-5]采用了SLM方法去降低PAPR。关于SLM方法,多种序列(比如,Walsh序列[4],Pseudo Random Interferometry 码[5]可用作该方法中的相位矢量。相比于传统SLM方法中随机产生的相位,使用这些序列后,PAPR会有小幅的降低。文献[6]提出了RS-SLM的改进算法,在IFFT(inverse fast Fourier transform)之前选择随机性最好的一个序列进行传输,依据是随机性越好,频谱越平坦,那么出现峰值的概率就越小。该方法可大大降低计算量以及复杂度,但是PAPR略有恶化。在文献[7]中先产生了不同的序列组,然后,将这些序列以最小互相关为目的进行组合,把PAPR降低到5 dB以内。但是该方法中组合这些序列的计算量很大且较复杂。而文献[8]通过将IFFT计算分解,总结出SLM方法中的共有因子,仅仅需要一个IFFT运算,其他支路均可用简单的翻转和叠加来完成,从而大大降低了算法复杂度,但是没有额外的PAPR降低效果。文献[9]提出了一种SLM和PTS联合使用的方法,得到了比只使用其中一个方法更好的PAPR降低效果,但是,存在更大的复杂度和运算量。
本文对SLM作了改进,提出循环反馈SLM方法。本方法中首先采用了若干ZC(Zandoff-Chu)序列作为初始的相位旋转矢量,其后,根据PAPR比较结果的反馈信息进一步更新相位序列。仿真结果证明,该方法可有效降低PAPR。
1 OFDM系统简介
图1给出了OFDM系统基本原理框图。
尽管宽带无线信道不平坦且具有频率选择性衰落,但是经过串并变换将高速串行的数据流变为并行低速数据流之后,每个子载波是相对平坦的,并且信号带宽大于相干带宽从而可以有效地消除符号间干扰[10]。
一个OFDM符号是若干并行的调制子载波的叠加,其中,每个子载波可以是QPSK,16QAM 或者64QAM调制。然后,对这些已调制符号作N点IFFT,因而,一个OFDM符号可表示为

(1)式中:di是第i个子载波上的已调符号;N是子载波数。
OFDM符号s(k)的峰均比定义为其峰值功率与均值功率的比值。
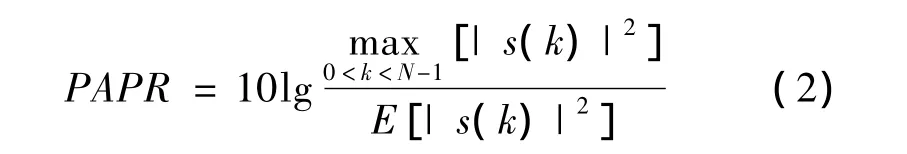
(2)式中:|s(k)|是信号的瞬时功率;E[·]表示期望值。
对于QPSK调制,根据中心极限定理,当子载波数N足够大时,符号s(k)的实部和虚部均服从高斯分布。s(k)的幅度服从瑞利分布,其概率密度函数可表示为pa(t)=2r e-r2。s(k)的功率服从2个自由度的中心 χ2分布,其概率密度函数[11]为 ppower(y)=e-y。
具有N个子载波的OFDM符号的PAPR大于某门限值z的概率可表示为
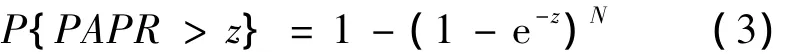
(3)式就是PAPR的互补累积分布函数(complementary cumulative distribution function,CCDF)。通常用CCDF来衡量PAPR的分布[12]。
通常,连续时间信号经过奈奎斯特采样之后,就不能得到其准确的PAPR值。因此,我们采用过采样来得到更加接近连续信号的PAPR值。仿真结果表明,当采用大于4倍的过采样时,PAPR值与连续时间信号的PAPR值基本一致。本文中我们采用4倍过采样。
2 SLM方法的原理


图2 SLM方法处理框图Fig.2 Block diagram of SLM method
3 循环反馈SLM算法
本文提出的循环反馈SLM方法,以ZC序列作为初始相位基序列,对于传统SLM方法中的每个子块不再固定其相位矢量,而是根据PAPR比较结果的反馈做出相应的相位矢量调整。ZC序列是属于CAZAC(constant amplitude zero auto-correlation,CAZAC)序列即恒幅零自相关序列的一种,具有CAZAC序列的一些共有特性。比如,幅度恒定,且DFT(discrete Fourier transform)变换之后仍保持常幅。幅度恒定可限制大PAPR的出现并减少对其他用户的干扰。其次是周期自相关性,即不同长度的ZC序列有理想的循环自相关特性。

图3给出了循环反馈SLM算法的处理框图。

图3 循环反馈SLM方法处理流程框图Fig.3 Flow chart of new SLM method with feedback searching
由图3可将该算法总结为如下具体步骤。

步骤2 将步骤1中所使用的相位矢量的首个元素乘以“-1”,因此,可得到一个修正相位矢量,用此修正相位矢量乘以输入数据X,IFFT之后计算其PAPR,标记此PAPR为papr。
步骤3 比较第1步中的PAPRmin和步骤2中所得的papr。
如果papr>PAPRmin,将步骤2中所乘修正相位矢量的首个元素再乘以“-1”,即恢复为步骤1所使用相位矢量的元素。如果papr<PAPRmin,令PAPRmin=papr。
步骤4 再将步骤3中经过调整的相位矢量的下一个元素乘以“-1”,作IFFT变换之后计算其PAPR,并令 papr等于此 PAPR。然后,作如步骤3的比较和反馈调整。
步骤5 依次将步骤1中所用相位矢量中的元素作如步骤2到步骤3的调整,从而可得到子块1中具有最小PAPR值的选择序列及其最小PAPR值。
步骤6 对子块2至子块D作如子块1从步骤1至步骤5的处理,分别得到各个子块中具有最小PAPR值的选择序列及其相应的PAPR值。
步骤7 对以上得到的D个选择序列再次进行比较得到具有最小PAPR的序列及其所使用的相位矢量,将此序列及相位矢量信息发送至接收机。
从以上具体步骤中可以看出,每个子块中所乘的相位矢量不再是固定不变的某个矢量,而是根据PAPR值比较结果的反馈进行调整,若乘以“-1”翻转后,PAPR值变大,则恢复其原来相位矢量的元素;若PAPR值降低,则保留翻转,并对下一个元素逐个作翻转比较。
4 仿真结果及其分析
本文采用的仿真环境是AWGN信道,输入数据进行4倍过采样。在发送端假设采用TWTA(travelling wave tube amplifier)[14]作为非线性大功率放大器。未特别说明则其输入补偿值(input back off,IBO)为6 dB。
图4给出了采用不同子块数(D=1,2,4)的循环反馈SLM时,OFDM符号的峰均比值的CCDF分布仿真图。其中,子载波数目是64,每个子载波采用QPSK调制。从图 4可知,当子块数为 1,且CCDF=10-3时,与原始OFDM符号相比,循环反馈SLM算法可带来大约4 dB的PAPR改善(图4中已标出)。由图4可知,D=2时的CCDF曲线与D=4时的差距小于D=2与D=1时的差距。可得到,随着子块数的增加,PAPR仅以小幅度降低,但算法复杂度却大大增加。所以,与传统的SLM方法比起来,本文提出的改进的循环反馈SLM中子块数目不必过大,设定D=1或D=2也可以得到PAPR特性的有效改进。
图5是采用循环反馈SLM之后系统BER(bit error rate)曲线和传统OFDM系统BER曲线的比较。其中,载波数目为64,采用QPSK调制,且循环反馈SLM算法采用的子块数为1。图5分别绘出了理论BER曲线以及放大器补偿分别为0 dB和6 dB时,加入循环反馈SLM和未加入降低峰均比算法的BER性能仿真曲线。从图5中可看出,放大器补偿值增加,则系统BER性能得到改善,而且加入循环反馈SLM方法后的系统性能与未加入该算法的传统OFDM系统相比有很明显地改善。在图5中,当BER=10-4,放大器补偿为6 dB时,采用循环反馈SLM方法的系统得到大约2 dB的SNR(signal to noise ratio)增益(图5中已标出)。

图4 采用循环反馈SLM的OFDM符号峰均比的CCDF分布仿真图Fig.4 CCDF of PAPR of OFDM symbols using SLM with feedback searching

图5 采用循环反馈SLM的OFDM系统BER性能Fig.5 BER of OFDM system using SLM with feedback searching
5 总结
本文改进降低OFDM信号峰均比的SLM方法,提出了以ZC序列作为初始相位旋转矢量的循环反馈SLM算法。在该算法中,每个子块的相位矢量不再是固定不变的,而是根据峰均比比较反馈信息并循环更新。仿真从2个方面对该算法的有效性进行分析:PAPR的CCDF分布以及BER性能。仿真结果表明,循环反馈SLM方法可有效地降低OFDM信号的PAPR值,因而来自非线性器件的信号非线性失真较小从而明显地改善系统的BER性能。此外,跟传统的SLM方法相比,本文提出的改进的循环反馈SLM中子块数目不必过大,即使设定D=1或D=2也可以得到PAPR特性的有效改进。
[1]HUA Y,GANG W.Choosing the optimal clipping ratio for clipping and filtering PAPR-reduction scheme in OFDM[C]//Wireless Communications,Networking and Mobile Computing,WiCom 2007.ShangHai:Conference publications,2007:460-463.
[2]TAO J,ZHU G X.Complement block coding for reduction in peak-to-average power ratio of OFDM signals [J].Communications Magazine,IEEE,2005,43(9):17-22.
[3]徐明,张德民.一种低复杂度的降低OFDM峰均功率比的PTS方法[J].重庆邮电大学学报:自然科学版,2007,19(4):476-480.
XU Ming,ZHANG Deming.A low complexity PTSmethod for reducing peak-to-average power ratio ofOFDM[J].Journal of Chongqing University of Posts and Telecommunications:Natural Science,2007,19(4):476-480.
[4]RUANGSUTHINARUPAP S,AHMED K M,RERNANDOW A C.PAPR reduction by combining selected mapping and selected spreading code in MC-CDMA systems[C]//Computers and Communications 2004.Proceedings.ISCC 2004.[s.l.]:Conferece Publications,2004:725-729.
[5]WANG JZ,LUO JY,ZHANG Y L.A new phase sequence for SLM in MC-CDMA system[C]//Wireless Communications, Networking and Mobile Computing,2007.WiCom 2007.Shanghai:Conference Publications,2007:938-941.
[6]WANG D,XU L B.An improved SLMalgorithm for reducing PAPR in OFDM system[C]//Control,Automation and Systems Engineering(CASE).Singapore:Conference Publications,2011:1-3.
[7]WU Y,MAN K L,WANG Y.Optimum selective mapping for PAPR reduction[C]//Wireless Telecommunications Symposium(WTS).New York,city Ny:Conference Publications,2011:1-5.
[8]SOOBUM Cho,SANG Kyu park.A new selected mapping scheme without additional IFFT operations in OFDM systems[J].Consumer Electronics,IEEE Transactions on,2011(11):1513-1518.
[9]SINGH K,BHARTIM R,JAMWAL S.A modified PAPR reduction scheme based on SLMand PTS techniques[C]//Signal Processing,Computing and Control(ISPCC),2012 IEEE International Conference on.Waknaghat Solan:Conference Publications,2012:1-6.
[10]汪裕民.OFDM关键技术与应用[M].北京:机械工业出版社,2007:31-53.
WANG Yumin.OFDM Key technique and its application[M].Beijing:China Machine Press,2007:31-53.
[11]曾召华.LTE基础原理及关键技术[M].西安:西安电子科技大学出版社,2010:87-91.
ZENG Zhaohua.Fundamental theory and key technique of LTE[M].Xi’an:Publishing house of Xidian University,2010:87-91.
[12]YEN P,MINN H,CHONG C C.PAPR reduction for bandwidth-aggregated OFDMand SC-FDMA systems[C]//Wireless Communications and Networking Conference(WCNC),2011 IEEE.Cancun,Quintana Roo:Conference Publications.2011:1363-1368.
[13]曾召华.LTE基础原理及关键技术[M].西安:西安电子科技大学出版社,2010:263-264.
ZENG Zhaohua,Fundamental theory and key technique of LTE[M].Xi’an:Publishing house of Xidian University,2010:263-264.
[14]TRANTERW H,SHANMUGAN K S.Principles of communication system simulation with wireless applications[M].London:Prentice Hall,2004:290-300.
(编辑:刘 勇)

