卫星通信中一种改进的变步长LMS 均衡算法研究
魏 武,左天虎,刘期烈,黄 巍,李 云
(1.国家移动卫星通信工程技术研究中心,南京 210000;2.重庆邮电大学移动通信技术重点实验室,重庆 400065)
0 引言
作为当今通信领域的三大信息传输手段之一,卫星通信无疑是目前比较理想的一种用于实现长途通信的方式,在政治、经济和军事等诸多领域都有越来越广泛的应用,是现代通信系统的重要组成部分。在远距离传输的过程中,由于卫星系统中的非线性元器件和无线传输信道环境的影响,卫星通信过程容易产生非常严重的非线性失真。因此,对卫星通信过程中的码间干扰实现均衡是卫星通信过程中的关键技术之一,使用均衡器是当前一种普遍应用且非常重要的方法。由于无线信道的未知性和时变性等因素,卫星通信系统要求均衡器对信道特性的变化要能够随时地调整自身的抽头权系数,以适应信道特性的变化,所以,对卫星通信自适应均衡算法的研究成为实现这类自适应均衡器的关键。
自适应均衡技术的核心是均衡算法,主要包括最小均方误差(leastmean square,LMS)算法和递归最小二乘(recursive least squares,RLS)算法两大类。在 20 世纪 60年代,Windrow 和 Hoff[1-2]提出了基于LMS准则的LMS算法,由于这种算法具有计算量小、稳定性强、易于实现等优点而被广泛应用于自适应均衡、智能天线通信、声呐、雷达、系统辨识等诸多领域,但定步长 LMS(fixed step size LMS,FSS-LMS)算法不可能同时满足收敛速度和稳态误差性能。为了克服定步长LMS算法的这一缺陷,很多改进的LMS算法被提出,其中,大多数是变步长的 LMS(variable stepsize LMS,VSS-LMS)算法。这些算法基本都遵循以下原则:在算法的初始阶段或者是未知通信系统的参数发生变化时,取较大步长值,以得到较快的收敛速度和自动跟踪能力;在算法接近收敛稳定的时候,取较小的步长值,以取得较小的稳态失调误差。这些算法的区别在于使用不同的机制来改变步长值[3-11]。比如:文献[3]提出一种自动增益控制算法,文献[4]利用算法迭代产生的平方误差来构建步长迭代表达式,文献[5]引入了多个参数共同控制步长变化的方法,文献[6]通过估计平方误差来控制步长变化的大小,文献[7]研究了变步长LMS算法的稳定性问题,文献[8-9]根据步长的变化原则,构建了新的步长非线性表达式,文献[10]提出的基于 Sigmoid函数的变步长 LMS(sigmoid variable step-size LMS,SVSLMS)算法,可以提高收敛速度,但算法的步长函数表达式较复杂,且稳态时步长值变化较大,所以,稳态误差较大。针对Sigmoid函数在算法稳态时的微小误差仍产生较大步长的情况,文献[11]对该算法进行了改进,提出了改进算法(G-SVSLMS算法),但该算法仍然是基于Sigmoid函数,需要进行指数运算,复杂度大。文献[12]提出的基于箕舌线的变步长LMS算法,收敛速度快,接近稳态时步长曲线平滑,稳态误差较小。SVSLMS,G-SVSLMS和箕舌线LMS算法均是通过误差或者误差功率来调整步长值,这就会导致算法本身对噪声非常敏感。而评价一个算法好坏的因素主要有收敛速度、收敛时候的稳态误差、对时变系统的跟踪能力、抗噪声能力以及算法的复杂度。
本文提出一种改进的变步长算法,引入一个递减的等比序列来表示步长的初始值,以此来替代传统的固定的值,从而得到初始时候的较大步长值和接近收敛时候的微小步长值,使算法在较低的信噪比环境下也能实现较快的收敛速度和较小的稳态误差。本文算法在稳态环境下拥有较快的收敛速度和相对较小的稳态误差,同时具有较好的抗噪声性能。应用到卫星通信系统中,能有效改善系统的误码性能。
1 传统LMS算法
1.1 FSS-LMS算法
最速下降法是一种最基本的搜索方法,也是一种递归算法,其基本思想是将代价函数看成是滤波器的权向量的函数,通过令代价函数取得最小值来找到此时的权向量,也就是此线性滤波器的最优解。定步长LMS算法是在最速下降法的基础上发展起来的一种新的算法,二者在原理和滤波器结构上都非常相似,在代价函数上却存在很大差别。最速下降法使用均方误差作为目标的代价函数,由于这种方法需要知道输入信号的自相关矩阵以及输入信号和期望信号的互相关矩阵等先验信息,所以,每次迭代的梯度向量是很难准确测量的。于是,LMS算法直接使用瞬时的误差功率作为均方误差的估计值,然后,使用递推迭代的方式,使自适应滤波器逐步趋向最佳的维纳解,从而大大减少了运算量。
自适应滤波器主要由抽头权系数可调的数字滤波器和自适应滤波算法组成,其原理如图1所示。图1中,x(n)为n时刻的输入信号;y(n)为输出信号;d(n)为期望输出信号;v(n)为噪声信号;e(n)是期望输出信号d(n)和输出信号y(n)之间的误差信号估计;而LMS算法则是通过e(n)来调节滤波器的抽头系数,使滤波器收敛至稳态。

图1 自适应滤波仿真结构示意图Fig.1 Adaptive channel equalization model

(1)-(2)式中:参数与图1中的参数一致。(1)式中输入信号xT(n)和滤波器抽头系数乘积表示滤波器的系统输出信号。(3)式中:w(n)是滤波器n时刻各抽头的权系数;μ是步长因子,是控制算法收敛速度和收敛性能即稳态误差的参量,其取值为0<μ <1/λmax,λmax是输入信号 x(n)的自相关矩阵的最大特征值。这里的步长因子是一个上述取值范围内的一个固定值。考虑到收敛速度和稳态误差这2个因素,步长值μ的选择不得不需要折中考虑,无论是取太大或者太小效果都不会理想。最理想的步长因子μ的选择策略是在算法的初始阶段,由于均方误差较大,步长因子μ应该选择较大值,以获取更快的收敛速度。随着滤波器的抽头系数越来越接近最佳的维纳解,也就是均方误差已经接近零的时候,此时的步长因子μ就应该取较小的值,以获得较小的稳态误差。正是因为需要这样变化地对步长因子μ取值,变步长算法的思想才被提出。
1.2 VSS-LMS算法
基于以上基本原则,各种变步长LMS算法被提了出来。如:基于Sigmoid函数的SVS-LMS算法以及在其基础上提出的改进算法,主要有将步长与e(n)2和e(n)e(n-1)建立非线性关系;将步长正比于误差大小或者与瞬时均方误差建立非线性关系;还有算法引入了遗忘因子,从而使步长因子和前面的n个误差值有关,进而提高了算法的抗噪声能力。
以上提到的各种算法均具有良好的性能,其中最为经典的是基于Sigmoid的SVS-LMS算法和其改进形式的 G-SVSLMS算法。基于 Sigmoid的 SVSLMS算法的步长迭代公式为

(4)式中:β,α都是控制因子,其中,β为控制步长的最大取值,α为控制步长的变化速度。
VSS-LMS该算法的优点是具有较快的收敛速度和较强的时变跟踪能力,但是由于Sigmoid函数本身在自变量接近零的时候函数值仍然有较大的变化,不具备缓慢变化的特性,导致了算法收敛后,步长因子μ变化范围较大、速度较快而存在较大的稳态误差。在此算法基础上提出的G-SVSLMS算法,其步长因子的迭代公式为

G-SVSLMS算法在大大减少了计算量的基础上,在误差e(n)接近零的时候具有缓慢变化的特性,克服了SVS-LMS算法在收敛阶段步长因子变化仍然较大的缺陷。同时,G-SVSLMS算法还具有较快的收敛速度,但是,由于算法仅仅与当前的误差e(n)有关,抗噪声能力不强,主输入端的噪声对算法的性能影响较大,在信噪比较低的环境下,算法的精度易受到影响。
2 改进的变步长LMS算法
本文在上述算法的基础上,提出了一种改进的变步长LMS算法,其主要思想是引入一个递减的等比序列,使步长因子在算法初始阶段可以取得较大值,以求快速收敛,在稳态阶段保持较小的步长值,以取得较小的稳态误差;同时,引入当前时刻的误差和前一时刻误差的绝对误差,一方面可以有利于取得较小均方误差;另一方面可以增强算法的抗噪声性能。其步长迭代公式为
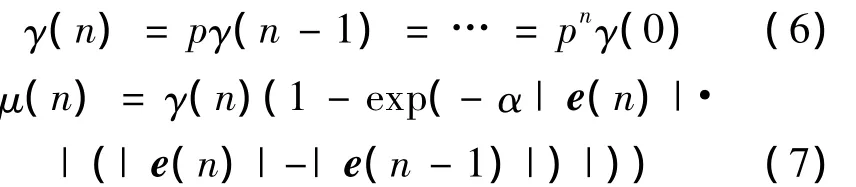
(7)式中:α是步长函数的斜率因子,控制步长函数图形的形状;γ(n)为步长函数的幅度因子,γ(n)是按照(6)式表示的递减等比序列逐渐递减。(6)式中,p表示衰减系数。在(7)式中引入γ(n)后,由于算法迭代初期迭代次数有限,衰减系数p取接近1的正常数,γ(n)可以保持较大值,同时,由于算法初始阶段的误差值e(n)较大,(7)式等号最右边括号内部的取值会比较大,二者共同作用下,可以使步长因子取得较大值,得到较快的收敛速度。当算法接近稳态时,γ(n)的取值也由于迭代次数的增加而变小,且变化速度也会变得缓慢,而由于此时的误差e(n)取值变小,所以,(7)式等号最右边括号内部的取值也变小,两者共同作用下,步长因子可取得较小值,且变化速度较缓慢,有利于取得较小的稳态误差。
图2是 γ(0)分别取值[1,0.8,0.6,0.2]的时候,步长因子μ(n)与误差e(n)之间的映射关系图。由图2可知,当γ(0)的取值越大,步长因子的初始值越大,算法收敛速度越快,在误差e(n)接近0时的取值变化也较快,反之,γ(0)取值越小,步长因子的初始值越小,算法收敛速度越慢,在误差e(n)接近0时的取值变化也较慢。
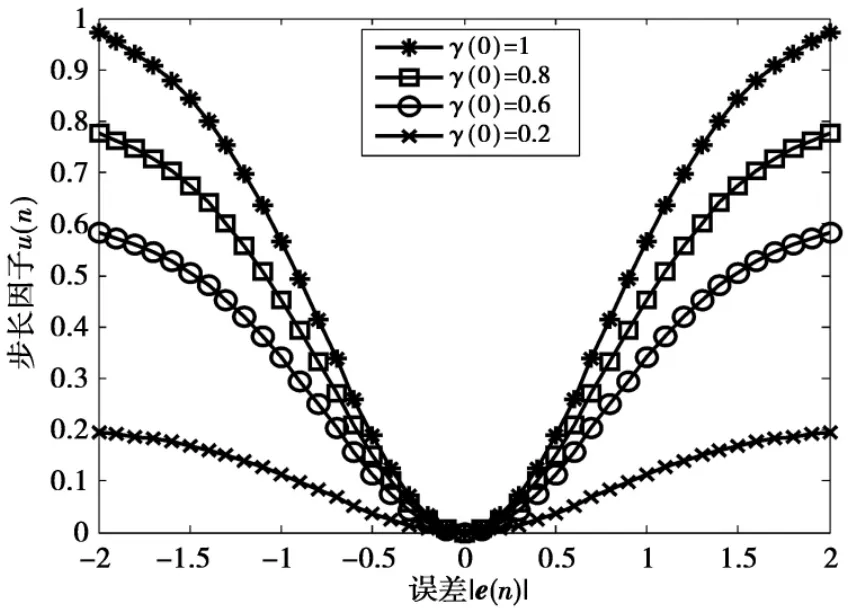
图2 γ(0)变化,p=0.99,α =1时|e(n)|与 μ(n)的关系图Fig.2 μ(n)varieswith|e(n)|,while p=0.99,α =1,γ(0)changes
图3是 p分别取值[0.99,0.9,0.7,0.5]的时候,步长因子μ(n)与误差e(n)之间的映射关系。可以看出,衰减系数p取值越大,越有利于取得较大的步长因子,但是当误差e(n)接近0时,步长因子幅度衰减的速度越快,p取值越小,当误差e(n)接近0时,步长因子幅度衰减速度越慢。可以说p是控制曲线取值变化的重要参数,是步长曲线在误差e(n)接近0时取得缓慢变化的低步长值的关键。图4反应了α的不同取值对步长函数形状的影响,α取值太大时,曲线开口很小,步长斜率太大,在e(n)接近零的时候,步长值仍然较大,且变化很快,这必然造成稳态误差增大;α取值过小,曲线开口太大,步长较小且变化缓慢,收敛速度减慢,十分不利于快速收敛和快速跟踪。

图3 p变化,γ(0)=1,α =1 时|e(n)|与 μ(n)的关系图Fig.3 μ(n)varies with|e(n)|,while γ(0)=1,α=1,pchanges
由以上分析可知,本文算法稳态时,步长变化平滑缓慢,克服了前文SVS-LMS算法在e(n)接近零时步长变化太大的缺陷。所以,步长因子的取值和变化由γ(0),p和α共同确定,如果要获得较快的收敛速度,则3个参数都应该取较大值;如果要取得较小的稳态误差,则3个参数都应该取较小值,但是具体的取值情况应该根据实际应用环境来确定最佳的取值。

图4 α 变化,γ(0)=1,p=0.99时|e(n)|与 μ(n)的关系图Fig.4 μ(n)varieswith|e(n)|,while γ(0)=1,p=0.99,α changes
另外,为了加强算法的抗噪声性能,在误差向量自相关运算的基础上,引入当前时刻的误差和前一时刻误差的绝对误差|(|(e(n)|-|e(n-1)|)|来调节步长,一方面由于引入前一时刻的误差而使得步长迭代不仅仅与当前的误差有关,这就有效减弱了算法容易受噪声影响,增强了算法的抗噪声性能;另一方面,用绝对误差而不是瞬时误差,利用二者绝对取值的绝对差值会进一步小于此时的瞬时误差的取值,有利于取得更小的步长值,进而取得更小的稳态误差。
2.1 抗噪声性能分析
为了减小计算的复杂度,算法使用当前时刻和前一时刻的误差乘积e(n)e(n-1)来表示E{e(n)·(e(n)-e(n-1))},设自适应均衡器的抽头权向量的最佳维纳解为w0,此时自适应均衡器的输出与期望输出之间的差值为ξ(n),则:设噪声功率为σ2,则由系统特征可知


比较(14)式和(15)式可知,误差的自相关函数只与输入信号有关,而与噪声无关。所以,本文算法具有较强的噪声抑制能力。
2.2 算法复杂度对比
考察一个算法的好坏,不仅要考察到性能的改善,还需要知道得到这种性能改善后该算法的计算复杂度如何。以算法总共进行的乘法和加法运算次数来表示,则LMS算法由于其结构最简单,所以,复杂度最低,G-SVSLMS算法和文献[13]算法一致,与本文算法相当,所以,本文算法在提高算法性能的同时,也基本保持了算法原来的复杂度,达到了算法改进的效果和目的。表1表示上述几种算法的计算复杂度。

表1 4种算法的计算复杂度Tab.1 Computation complexity of the four algorithms
3 仿真及结果分析
3.1 仿真参数配置
通过Matlab仿真来比较本文算法和其他算法的性能。仿真条件如下:自适应滤波器阶数M=5,不妨将卫星通信系统模拟成为FIR滤波器,其系数权向量 w=[0.4,0.6,1,0.6,0.4]T,输入信号 x(n)为零均值、方差为1的高斯随机信号,噪声v(n)为零均值,且与x(n)不相关的高斯白噪声,信噪比分别取25 dB和8 dB。总共实验1 000次,每次采样500个点,学习曲线取1 000次实验的平均结果。
本文在上述实验条件下对各种算法进行了大量的仿真,测定了各种算法达最优性能时的最佳取值范围。各种算法的最优时刻具体参数取值如下:FSS-LMS算法的固定步长因子 μ=0. 05;在 G-SVSLMS算法中,α=100,β=0. 05;在文献[13]算法中,μmax=0.08,α =1 000,β = 150;在本文算法中,p=0.99,γ(0)=0.3,α =50。
3.2 仿真结果分析
图5是在 SNR=25 dB时,本文算法与 FSSLMS,G-SVSLMS和文献[13]中算法的误差性能和收敛速度比较图,图5中,各曲线为1 000次试验的学习曲线平均值。

图5 本文算法与文献[13]算法、FSS_LMS,G_SVSLMS算法比较(SNR=25 dB)Fig.5 Performance comparison between our algorithm and other algorithms with SNR=25 dB
由图5可知,本文算法的收敛速度略快于FSSLMS,G-SVSLMS和文献[13]中算法,大约在 70次迭代的时候就达到收敛状态,能够达到快速收敛的目的。算法收敛阶段的稳态误差方面,G-SVSLMS算法略低于FSS-LMS算法,达到10-2dB以下,文献[11]中算法明显低于上述2种算法,而本文算法明显低于上述3种算法,稳态误差最接近10-3dB,能够满足较小稳态误差的要求。
图6是SNR=8 dB 时,本文算法与FSS-LMS,GSVSLMS和文献[13]中算法的误差性能和收敛速度比较图,图6中,各曲线为1 000次试验的学习曲线平均值。

图6 本文算法与文献[13]算法、FSS_LMS、G_SVSLMS算法比较(SNR=8 dB)Fig.6 Performance comparison between our algorithm and other algorithms with SNR=8 dB
从图6可知,当SNR下降到8 dB时,所有算法的收敛速度基本相同,可以快速收敛。但是稳态误差均快速增大,均从小于10-2dB上升到大于10-1dB以上。FSS-LMS算法增加最快,G-SVSLMS算法次之,FSS-LMS算法大约在10-0.7dB 和10-0.8dB 之间,G-SVSLMS算法达到 10-0.8dB,而本文算法仍然低于其他几种算法,可以满足较小稳态误差的要求。
综上所述,本文算法在高信噪比的环境下,收敛速度略快于其他5种算法,稳态误差最小,且明显小于之前的其他算法,在低信噪比的环境下,收敛速度仍然不比其他几种算法慢,但是稳态误差仍然明显小于其他算法。经验证,本文算法可以有效地抑制随机噪声对输入信号的干扰,在综合性能上优于上文的几种传统LMS算法,是一种性能较好的改进变步长LMS算法。
4 本文算法在卫星通信系统中的应用
卫星通信系统的仿真模型如图7所示。图7中,x(n)为原始基带信号;v(n)为等效的噪声信号;y'(n)为均衡输出信号;y(n)判决输出信号;e(n)为判决输出与均衡输出信号的误差值。

图7 卫星通信系统仿真模型Fig.7 Satellite communication simulation model
本文选取某卫星通信系统的传输系统参数,原始基带信号的符号速率为300 M符号/s,卫星群时延在2倍奈奎斯特带宽内为6 ns,调制方式为QPSK,数据总量为106个,然后,将本文的新算法应用到上述系统的自适应均衡器中,仿真得到的误码率比较如图8所示。
由图8可以看出,原始基带信号经过卫星传输信道后,产生了严重的码间干扰,致使经系统均衡前的误码率非常大,严重影响通信质量。经过基于本文算法的自适应均衡器均衡之后,系统的误码率性能明显得到了较大的改善。有效验证了本文算法的可行性。
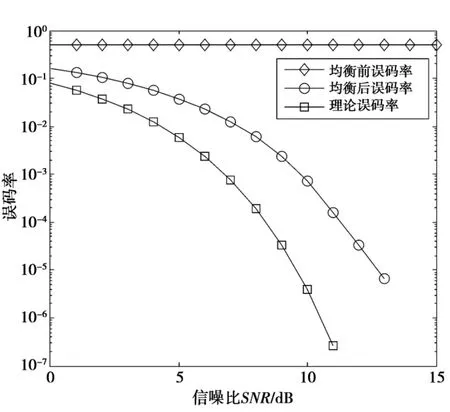
图8 误码率比较图Fig.8 Comparison of error data
5 结论
本文通过引入递减等比序列代替固定常数和在估计误差的自相关的基础上用绝对误差代替前一时刻瞬时误差,二者共同作用,既可以控制步长因子,使其在算法初始阶段可以取较大值,收敛速度快,在接近收敛的时候,取较小值,稳态误差较小,还可以有效地抑制系统噪声对信号的干扰。仿真结果显示,在高信噪比和低信噪比环境下,本文算法在初始收敛速度、稳态误差和抗噪声性能等性能指标上均优于几种传统的LMS算法。在卫星通信系统中,具有良好的应用前景。
[1]WIDROW B,HOFFM E.daptive switching circuits[EB/OL].[2013-12-10]http://www-isl.stanford.edu/people/widrow/papers/c1960adaptiveswitching.pdf.
[2]WIDROW B,McCOOL JM,LARIMORE M G,et al.Stationary and nonstationary learning chara-cteristics of the LMS adaptive filter[J].Proceedings of the IEEE,1976,64(8):1151-1162.
[3]SHAN T J,KAILATH T.Adaptive algorithms with an automatic gain control feature[J].Circuits and Systems,IEEE Transactions on,1988,35(1):122-127.
[4]ABOULNASR T,MAYYASK.A robust variable step size lms type algorithm:Analysis and simulations [J].IEEE Trans on Signal Processing,1997,45(3):631-639.
[5]LIYan,WANG Xinan.A Modified VS LMSAlgorithm.The 9th International Conference on Advanced Communication Technology[EB/OL].[2013-12-10]http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=4195210.
[6]KWONG R H,JOHNSTON E W.A variable step size LMSalgorithm[J].IEEE Trans Signal processing,1992,40(7):1633-1642.
[7]GEL FAND SB,WEIY KROGMEIER JV.The stability of variable step size LMS algorithms[J].IEEE Trans on Signal Processing,l999,47(l2):3277-3288.
[8]华强,夏哲雷,祝剑英.一种改进的变步长LMS自适应滤波算法及其仿真[J].中国计量学院学报,2012,23(3):304-308.
HUA Qiang ,XIA Zhelei,ZHU Jianying.A Modified variable step size LMS adaptive filtering Algorithm and its simulation [J].Journal of China University ofMetrology,2012,23(3):304-308.
[9]杨晓波.一种新的变步长LMS自适应滤波算法及分析[J].科技视界,2012(21):28-30.
YANG Xiaobo.A New Modified Adaptive LMSFilter Algorithm and anlyze.Science& Technology Vision,2012(21):28-30.
[10]覃景繁,欧阳景正.一种新的变步长 LMS自应用滤波算法[J].数据采集与处理,1997,12(3):171-174.
QIN Jingfan,OUYANG Jingzheng.A Novel Variable Step Size LMSAdaptive Filtering Algorithm Based on Sigmoid Function.Journal of Data Acquisition & Processing,1997,12(3):171-174.
[11]高鹰,谢胜利.一种变步长 LMS自适应滤波算法及分析[J].电子学报,2001,29(8):1094-1097.
GAO Ying,XIE Shengli.A Variable Step Size LMSAdaptive Filtering Algorithm and Its Analysis[J].ACTA ELECTRONICA SINICA,2001,29(8):1094-1097.
[12]邓江波,侯新国.一种新的变步长 LMS自适应算法及其性能分析[J].电声技术,2004(12):4-6.
DENG Jiangbo,HOU Xinguo.A Novel Variable Step Size Adaptive Filtering LMSAlgorithm and Its Properties Analysis[J].Elementary Electroa-coustics,2004(12):4-6.
[13]李海滨,韩延光,庄述燕,等.卫星高速宽带数传系统的变步长LMS均衡算法研究[J].宇航学报,2011,32(6):1423-1427.
LI Haibin,HAN Yanguang,ZHUANG Shuyan,et al.A Modified Variable Step LMSAdaptive Filtering Algorithm for Satellite High-Speed Broadband Digital Transmission System[J].Journal of Astronautics,2011,32(6):1423-1427.
(编辑:刘 勇)

