基于母弹弹道诸元误差值的自适应开舱方法
杨瑞伟,殷跃强,李东光,2,杨登红
(1. 北京理工大学 机电学院,北京100081;2. 北京理工大学 机电动态控制重点实验室,北京100081)
0 引言
子母弹是以毁伤面目标为主的常规弹药,具有瞬时火力密集、覆盖面积广、毁伤效能大等特点,主要用于攻击坦克群、装甲战车群、部队集结地、机场跑道等大面积目标。然而在母弹实际飞行过程中,由于受到发射初始弹道诸元误差、气象条件误差等的干扰,使得母弹飞行的弹道会偏离预定的理想弹道,如果仍然采用定时开舱,将导致子弹药的落点散布中心出现偏差,从而降低了子母弹的毁伤效能。因此,提高子弹药落点散布精度成为了子母弹研究的重点问题之一。本文针对旋转稳定子母弹建立子弹药的全弹道模型,对母弹弹道轨迹上预定开舱点之前的某位置处弹道诸元实际值与理论值的误差造成的子弹药落点精度影响进行仿真分析,提出了一种基于修正开舱点的开舱控制方法,以达到提高子弹药落点精度的目的。
1 全弹道模型的建立
母弹外弹道模型采用文献[1]的旋转稳定弹6 自由度的刚体弹道模型,抛撒方式则采用燃气推动活塞抛撒子弹药后抛的方式[2],在母弹到达开舱点后,利用燃气的推力将子弹药从母弹尾部逐层推出,并借助母弹高旋转产生的离心力作用让子弹分散。
设子弹在母弹中的排列为nl层,每层有ns个子弹,围绕中间的圆柱形支杆成环形紧密相接排布。如图1 所示。

图1 子弹药在母弹中的排布Fig.1 Configuration of submunitions in shrapnel
由于在抛撒过程中,子弹只能相对母弹弹体沿弹轴方向滑动。因此在弹轴坐标系中对子弹运动状况进行分析,在母弹弹轴方向子弹药运动方程为

式中:mk为第k 层所有子弹的质量;Fg,e为重力Fg沿母弹弹轴方向分力;Fp,e为火药推力Fp沿母弹弹轴方向分力;GM,e为子弹所爱的惯性力GM沿母弹弹轴方向分力;Rg为子弹受重力作用产生的摩擦力;Rs为母弹体内所有子弹在离心惯性力作用下产生的轴向摩擦力;第i 层第j 颗子弹药在离心惯性力作用下产生的轴向摩擦力;S 为母弹横截面积;p 为火药气体产生的压强。
该内弹道模型充分考虑了子弹药在母弹内部运动时主要的受力情况,并且能将每一层子弹药在出母弹弹体时沿母弹轴向的速度分离出来,较为准确地反映了母弹抛撒时的真实情况。
统一以地面坐标系为参考坐标系。其中母弹的速度vm由文献[1]中母弹弹道运动方程解算得出。子弹的抛射速度vs始终沿弹体向后,即在弹轴坐标系内

将该速度向地面坐标系转换得到vs[3].
对于第j 层、第i 个子弹来说,由母弹旋转引起的子弹切向速度voτ在弹轴坐标系内为

式中:vt为该时刻母弹旋转的切向速度值,由母弹弹道方程求解得出;ε1为随机值。
将以上各个速度向地面坐标系中投影,最终得到子弹抛撒时的速度矢量为

通过该模型可以精确得到每一发子弹药在离开母弹弹体时的速度大小和方向,这样便可以对所有子弹药的落点进行仿真计算,得到子弹药群的落点分布情况。
2 子弹药落点精度分析
取文献[3]中旋转稳定子母弹的一组初始诸元值(母弹出炮口时的飞行速度v0=685.3 m/s,转速n0=175.48 r/s,初始射角为θ0=45°,子弹药在母弹内共有6 层,每层7 发)作为理想值,母弹飞行过程气象条件为标准条件,开舱点为母弹弹道下降段离地面高度为2 000 m 的位置,此时的子弹药落点散布为理想散布情况(见图2 中的圆圈点)。

图2 母弹抛撒子弹药落点散布图Fig.2 Spread of submunitions dispersed from shrapnel
若设这些子弹药落点的坐标值分别为(x1,z1)、(x2,z2)、…、(xn,zn),则任意一个点(pn,qn),它与所有子弹药落点坐标值的距离sn[4-5]为

sn为一系列数的集合,若其中存在一个最小值sm,则将其对应的坐标系中的点P0作为子弹药落点散布的中心位置。P0(x)为该位置x 轴方向坐标值,P0(z)为该位置z 轴方向坐标值。如无特殊说明,下文所提到的子弹药落点散布中心位置皆为该方法确定的点。
然而实际发射中,子弹药出母弹炮口时的初速、射角的实际值与理想值相比存在正态随机误差值。加上气象实际条件与标准条件之间的误差,使得每一发母弹在飞行过程中任意时刻的弹道诸元实际值与该时刻理想值都不相同。如果仍取原来的开舱点,则子弹药落点散布会偏离理想情况。
在上述理想初始诸元值的基础上给初始速度与射角分别加上正态分布的误差值,取4 组初始发射数据,其实际子弹药落点散布见图2 中的三角点。仿真结果图能看出子弹药落点的散布受误差影响较大。因此,为提高子弹药散布精度需要对开舱点进行修正。
在本文的研究方法中,设母弹弹道下降段2 000 m高度对应的开舱点为预定开舱点,选取母弹弹道的下降段4 000 m 高度(未到达开舱高度)处弹道诸元实际值(包括x 轴方向速度vx、y 轴方向速度vy、z 轴方向速度vz、x 轴方向位置x 以及z 轴方向位置z)与理论值的误差,分析诸元误差对子弹药落点精度的影响,并依据该误差值对开舱点进行修正。
给文献[3]中的理想发射初始值分别加上满足各自正态随机误差值变化范围的最大误差值以及2 m/s 的横风、纵风值,得到母弹在下降段4 000 m处实际弹道诸元值的变化范围如表1.

表1 4 000 m 高度对应的弹道诸元理想值和实际值范围Tab.1 The ideal and practical value ranges of trajectory data at 4 000 m height
2.1 x 轴方向速度误差对子弹药落点精度分析
根据表1 的各诸元值变化范围,利用控制变量法对各参数进行分析。取4 000 m 高度处理想弹道诸元值,将x 轴方向速度值加入微小扰动值,得出的子弹药落点位置如表2.
由表2 可以看出,x 轴速度越大,子弹药落点的x 轴均值也越大,每1%的速度误差造成的子弹药落点误差范围在20 ~28 m 左右。z 轴落点值也有明显的变化,每1%的速度误差造成的子弹药落点误差范围在10 ~20 m 之间。

表2 不同x 轴速度下子弹药在x、z 轴落点均值比较Tab.2 Comparison of impact points of submunitions in x and z axes at different x-axis velocities
2.2 y 轴方向速度误差对子弹药落点精度分析
y 轴方向速度加上扰动误差后的子弹药落点位置如表3. 由表中看出每1%的速度误差使子弹药x轴方向落点偏差约为7 ~12.5 m 左右,而对z 轴均值偏差约为2 ~4.5 m 左右。可见y 轴速度对子弹药落点的影响比较小。

表3 不同y 轴速度下子弹药在x、z 轴落点均值比较Tab.3 Comparison of impact points of submunitions in x and z axes at different y-axis velocities
2.3 z 轴方向速度误差对子弹药落点精度分析
由表4 可知,每0.5 m/s 的初始z 轴速度偏差使子弹药的x 轴落点偏离在3 m 以内,即1%的速度误差造成的子弹药落点误差范围是1.5 m 左右。同时每1%的速度变化带来的z 轴位置偏差1.2 m 左右。比x、y 轴误差带来的影响比重要小。

表4 不同z 轴速度下子弹药在x、z 轴落点均值比较Tab.4 Comparison of impact points of submunitions in x and z axes at different z-axis velocities
2.4 x 轴方向位置误差对子弹药落点精度分析
表5 反映了不同x 轴位置下子弹药落点位置坐标。由表格数据计算得出每1%的x 轴方向位置偏差产生的子弹药落点x 轴均值偏差约为100 m 左右,而z 轴均值偏差约为75 m 左右。可见该因素是修正的主要因素之一。
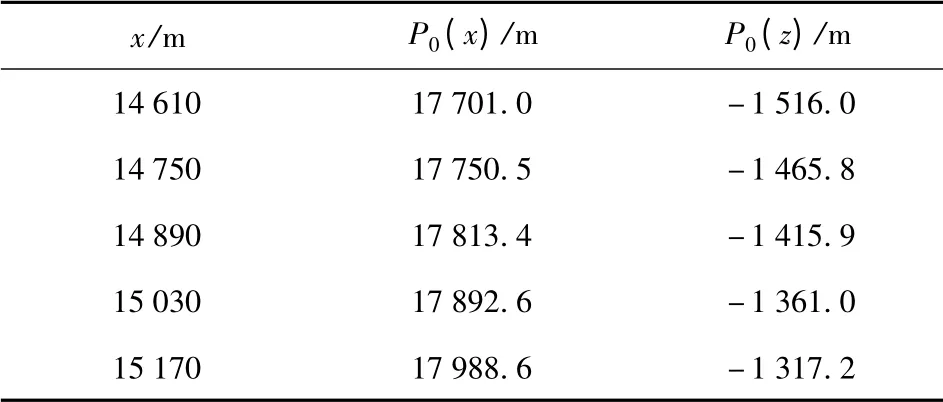
表5 不同x 轴位置下子弹药在x、z 轴落点均值比较Tab.5 Comparison of impact points of submunitions in x and y axes in different x-axis positions
2.5 z 轴方向位置误差对子弹药落点精度分析
z 轴方向位置加上误差后的子弹药落点位置如表6. 由表中看出每1%的z 轴位置误差使子弹药x轴方向落点偏差在40 m 左右,而对z 轴方向落点偏差约为20 m 左右。由此可见该误差因素也是对子弹药落点精度产生重要影响的因素之一。

表6 不同z 轴位置下子弹药在x、z 轴落点均值比较Tab.6 Comparison of impact points of submunitions in x and z axes in different z-axis positions
3 开舱点修正量算法
对于确定的子母弹系统而言,子弹药落点中心位置P0只与母弹飞行过程中的某位置处(本文取母弹下降段飞行高度为4 000 m 处)弹道诸元(速度诸元vx、vy、vz,位置诸元x、z)以及开舱点(因为母弹在下降段开舱点位置与所在高度值一一对应,因此本文将修正开舱点位置转化为修正开舱高度)有关。当4 000 m 处理想弹道诸元(vx0、vy0、vz0、x0、z0)确定时,子弹落点中心位置便与理想开舱高度h0对应,它们的函数关系[6-8]为

在实际子母弹发射过程中,由于初始发射误差、风速等误差因素的存在,使得每一发子母弹在4 000 m高度处弹道诸元实际值与理想值并不相同。若P1为实际子弹药落点中心位置,那么存在一个开舱高度差值Δh,使得修正后的P1离预定落点位置最近。即
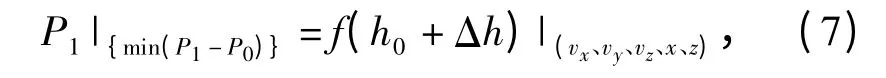
式中:vx、vy、vz、x、z 为实际4 000 m 高度处母弹弹道诸元。
由于预定落点位置对应的母弹飞行下降段4 000 m 高度弹道诸元值是固定的,所以(7)式中的开舱高度的差值只与4 000 m 处弹道诸元值相关,即有

将(8)式在理想弹道诸元值附近按泰勒公式展开得[9]

(9)式中c0值为0,表示当所有弹道诸元值都为理想值时,不用修正开舱高度。由(9)式可知,只需要分别求出每一个母弹下降段4 000 m 处弹道诸元值与理论值的误差值对开舱点修正量的大小,再将这些修正函数相加即可得到总的修正量。修正函数的系数可由大量的仿真数据拟合所得。
仍以第2 节提到的子母弹理想发射初始条件对应的4 000 m 高度处理想弹道诸元值(详细数值见表1)为例,在保持其他诸元误差值不变的情况下,对x 轴方向坐标值x=14 894.4 m 加上误差值,通过仿真找到对应落点偏差量最小的开舱高度,得到的结果如表7.

表7 x 轴位置误差对应的最佳开舱高度Tab.7 The best dispersing altitudes corresponding to different x-axis positions
由开舱高度修正值Δh 与其对应的x 轴方向坐标偏差值Δx,利用函数拟合得到对应的函数关系为

拟合结果如图3.

图3 P0(x)偏差值与高度修正值拟合图Fig.3 Fitting chart of corrected altitude values and x-axis deviation values
保持其他弹道诸元值不变,z 轴位置z = -848 m加上误差值,仿真得到的结果如表8.
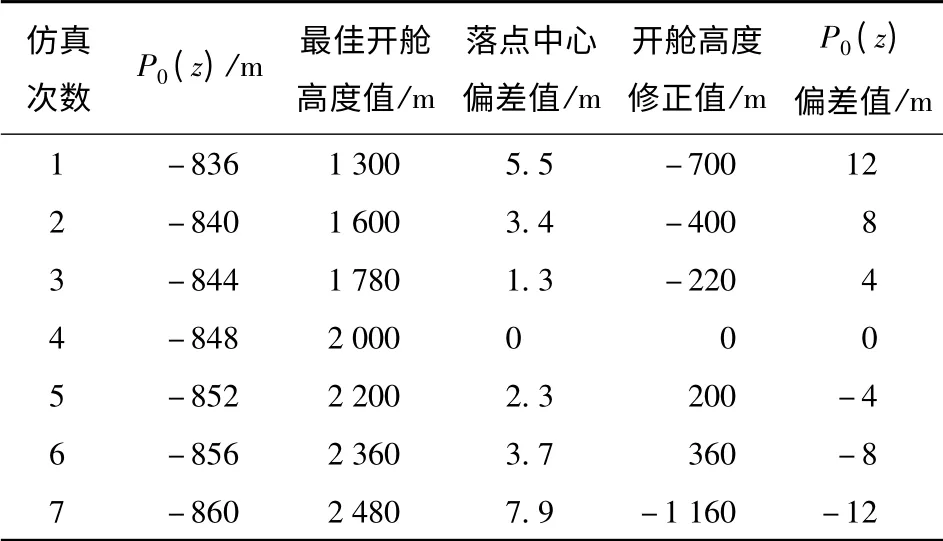
表8 z 轴位置误差对应的最佳开舱高度Tab.8 The best dispersing altitudes corresponding to different z-axis positions
由开舱高度修正值与其对应的z 轴方向坐标偏差值,利用函数拟合得到对应的函数关系为
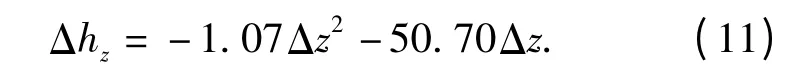
拟合结果如图4.

图4 P0(z)偏差值与高度修正值函数拟合图Fig.4 Fitting chart of corrected attitude values and Z-axis deviation values
用同样的方法分别求得4 000 m 高度处x、y、z轴方向上速度大小误差值与修正高度的关系,分别为

将(10)式~(14)式简单相加,得到所求的修正公式

此外在修正过程中,还需要考虑到子弹药散布情况,散布范围过大或者过小都会降低子弹药的毁伤效率,因此对应的修正后开舱点也应该有个最大最小的范围。以本文为例,对于(15)式需要加上条件限制[10-11]

式中:Δhmax、Δhmin值视具体需要的子弹药散布效果而定;Δh 为最终的开舱点修正量。
为验证修正方案的准确性,以第2 节的理想发射初始诸元为例,给初始速度和射角分别加上合理的服从正态分布的误差值正态随机变量,并在母弹飞行过程中加上合理的风速随机变化值,利用(15)式的修正方法,对7 发子母弹的开舱点进行修正,得到的未修正前子弹药散布中心位置分布与修正后子弹药散布中心位置分布见图5.

图5 修正前后子弹药落点散布图Fig.5 Distribution diagram of center positions of submunitions impact points before and after correction
图中三角点表示未修正的子弹药散布位置,圆圈点表示修正后的子弹药散布位置。由仿真结果计算可得未修正的子弹药落点的横向密集度为纵向密集度为修正后的子弹药落点的横向密集度为纵向密集度为则修正后横向密集度提高的百分比为

纵向密集度提高的百分比为

4 结论
本文通过对子母弹飞行过程的动力学分析,建立了从母弹飞行到开舱抛撒子弹药再到子弹药飞行的全弹道模型,并采用该模型对子弹药落点进行了仿真分析。通过母弹弹道开舱点前某位置处诸元误差值对子弹药落点精度影响的分析,得出了各个诸元差值对子弹药落点精度的影响情况,并提出了一种高旋转子母弹的自适应开舱方案,通过实例仿真计算得出了适用于该类子母弹的高度修正公式。结果表明修正后的横向密集度提高了26.3%,纵向密集度提高了53.8%.
References)
[1]杨启仁. 子母弹飞行动力学[M]. 北京:国防工业出版社,1999.YANG Qi-ren. Flight dynamics of cluster munition[M]. Beijing:National Defense Industry Press,1999. (in Chinese)
[2]谭大成,袁曾凤. 子母弹抛撒技术及其内弹道计算[J]. 北京理工大学学报,2000,9(3):273 -277.TAN Da-cheng,YUAN Ceng-feng. Cluster warhead dispering technique and its interior ballistic calculation[J]. Transactions of Beijing Institute of Technology,2000,9(3):273 -277. (in Chinese)
[3]Khalil M,Abdalla H,Kamal O. Dispersion analysis for spinning artillery projectile[C]∥13th International Conference on Aerospace Sciences and Aviation Technology. Egypt:Military Technical College,2009:ASAT-13.
[4]杨世荣,李小强,王才宏. 子母弹子弹落点模拟计算方法[J].火力与指挥控制,2008,33(4):87 -89.YANG Shi-rong,LI Xiao-qiang,WANG Cai-hong. Calculation method about placement simulation of submunitions dispersed from cluster munition[J]. Fire Control and Command Control,2008,33(4):87 -89. (in Chinese)
[5]赵水平,杨瑞伟,李东光,等. 子母弹自适应开舱引信控制系统设计[J].电子测量技术,2013,36(8):28 -32.ZHAO Shui-ping,YANG Rui-wei,LI Dong-guang,et al. Design of cluster bomb self-adaptive breaking out fuze control system[J]. Electronic Measurement Technology,2013,36(8):28 - 32. (in Chinese)
[6]王兆胜. 子母弹开舱高度的高低散布研究[J].火炮发射与控制学报,2012(2):21 -24.WANG Zhao-sheng. Research on vertical dispersion of opening height of carrier projectile[J].Journal of Gun Launch & Control,2012(2):21 -24. (in Chinese)
[7]游宁,马宝华. 火炮子母弹抛撒段子弹运动规律初探[J].兵工学报,1997,18(4):302 -307.YOU Ning,MA Bao-hua. Motion low of submunitions during dispersal time of cluster munition[J]. Acta Armamentarii,1997,18(4):302 -307. (in Chinese)
[8]杨正辉,李臣明,王晓鸣. 子母弹抛撒精度仿真分析[J]. 系统仿真学报,2009,21(9):2482 -2484.YANG Zheng-hui,LI Chen-ming,WANG Xiao-ming. Analysis andsimulation on cast precision of rocket with sub-warheads[J].Journal of System Simution,2009,21(9):2482-2484. (in Chinese)
[9]Verma V,Somani B.Accurate computation of ballistic trajectory using least square approximation with Crout’s method[C]∥International Advance Computing Conference. Patiala:IEEE,2009:305 -310.
[10]王兆胜,刘志强,刘全文. 子母弹射击精度的仿真研究[J].火力与指挥控制,2007,32(3):76 -78.WANG Zhao-sheng,LIU Zhi-qiang,LIU Quan-wen. Simulationstudy on firing accuracy of cargo-projectile[J]. Fire Control and Command Control,2007,32(3):76 -78. (in Chinese)
[11]唐克,崔卫兵,王存威,等. 基于Matlab 的影响子母弹抛撒精度的因素研究[J].指挥控制与仿真,2010(2):59 -61.TANG Ke,CUI Wei-bing,WANG Cun-wei,et al. Research on thefactor of influencing shrapnel spreading precision based on Matlab[J]. Command Control and Simulation,2010(2):59 -61. (in Chinese)

