混沌调频-调相MIMO雷达正交波形设计
王佳佳, 谢亚楠, 谭子苗
上海大学通信与信息工程学院,上海200072
MIMO雷达系统是一个多输入多输出的雷达系统装置,其发射端和接收端均有多根天线,可用来发射和接收信号.发射信号的波形对整个雷达系统的性能尤为重要,好的发射信号能降低整个雷达系统的截获性[1],从而提高雷达的战场生存能力.常用的离散形式正交发射信号有正交相位编码信号[2-4]、离散频率编码信号[5-7]、多载频信号等,连续形式的正交发射信号有连续的调频信号[8]等.
文献[9]首次将优化计算方法用于信号的波形设计,并根据模拟退火算法设计了具有良好相关特性的离散频率编码信号.文献[10]采用遗传优化算法设计相位编码的MIMO雷达信号,得到了一些性能较好的信号波形,但算法效率低,耗时长,而且当天线数目和码元长度改变时,算法复杂度有所增加.为了有效避免遗传算法中存在的早熟问题,文献[11]将模拟退火算法引入到遗传算法中,从而构成了新型的混合优化算法,提高了算法的收敛速度,同时得到了令人满意的波形.然而,当天线数目和码元长度增加时,不易得到所需要的波形.
由于混沌序列的取值具有初值敏感性和类随机性的特点,使用混沌序列在短时间内可以产生数量众多且干扰方无法掌握规律的编码信号,说明将混沌序列运用到频率和相位上是不错的思路.文献[2]把混沌序列映射到相位编码上,设计出的混沌相位编码信号具有良好的自相关和互相关特性,可用于MIMO雷达波形设计.文献[12]以混沌调频信号作为MIMO雷达的发射信号波形,利用混沌序列良好的统计特性得到了性能优越的正交波形集.本文则利用Bernouli单映射进行频率编码,将Logistic和Tent混沌函数交叉混合得到的序列进行相位编码,从而获得了复合混沌调频-调相编码信号.与单一调制信号相比,复合调制信号保留了相位调制信号的宽频谱特性和频率调制信号的抗干扰性能,同时采用复合混沌映射增加了信号的复杂性,大大减小了发射信号被敌方截获的概率.
1 调频-调相M IM O雷达信号
1.1 信号的模型
调频[8,12-13]-调相[2-4,10,14]MIMO雷达第l个波形第i个子脉冲信号的一般复数表达式为

式中,f0为载波频率,K为调制系数,为单混沌调制函数,⊗符号为卷积.是第l个波形第i个子脉冲信号的伪随机相位,其中M为相位编码可用的相位数,={0,1,···,M-1}表示第l个波形第i个子脉冲的伪随机相位指示.为了便于表示,在后面的分析中均去掉l和i,则调频-调相MIMO雷达信号复包络的表达式为
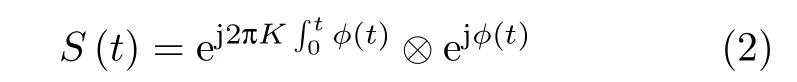
1.2 离散化的信号模型
为了便于处理和分析信号,对调频-调相MIMO雷达信号进行离散化,分别记为
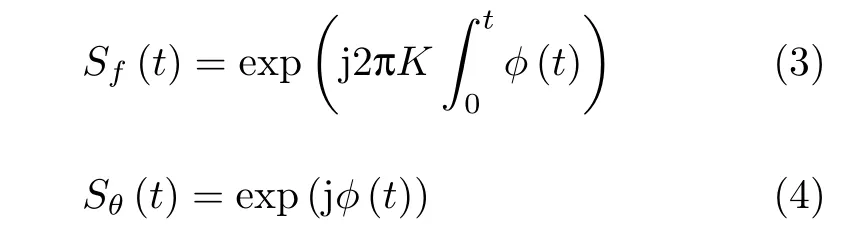
式(3)中的φ(t)可进一步表示为
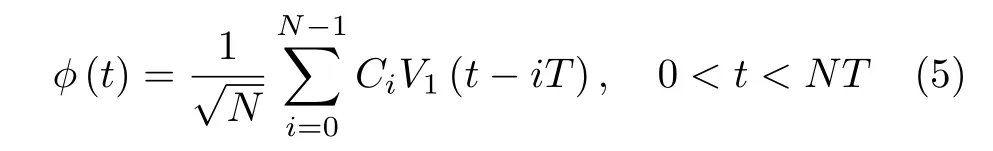
式中,V1(t)=0<t<T,Ci为单混沌函数映射后得到的编码序列,T为子脉冲宽度,N为编码长度,即子脉冲数目.
将式(5)代入式(3),同时根据矩形函数的性质可进一步化简为

式(4)可进一步表示为

式中,V2(t)=0<t<T,Cm为双混沌函数映射后的编码序列,可从ejn2π/M,n∈{0,1,2,···,M-1}中选择,在这里选择的相位调制的子脉冲宽度和频率调制的子脉冲宽度是一致的,均为T.这样选择是为了便于计算,当然也有不同的选择方法.
将式(6)和(7)代入式(2)可得

进一步将式(8)进行离散化处理.令采样间隔为T,那么有采样频率fs=1/T,即对每个子脉冲采样1次,则式(6)可表示为

根据式(1)可以得到频率调制函数的瞬时频率

由式(10)可知频率范围如下:f0+Kφ(t)min≤f≤f0+Kφ(t)max.依据奈奎斯特采样定理,采样频率大于等于调制信号的带宽,以及得到的混沌序列在[-1,1]之间,即|φ(t)|≤1,故采样频率需满足以下条件:
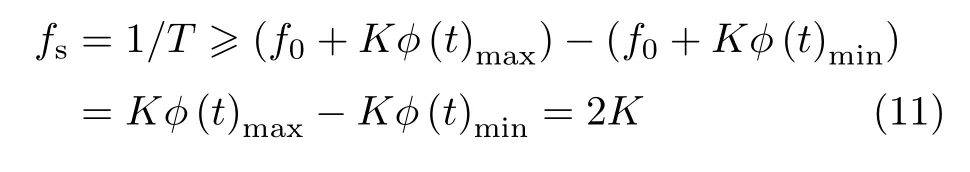
式中,取fs=1/T=2K,即K=1/2T,代入式(8)可得到调频-调相的离散形式
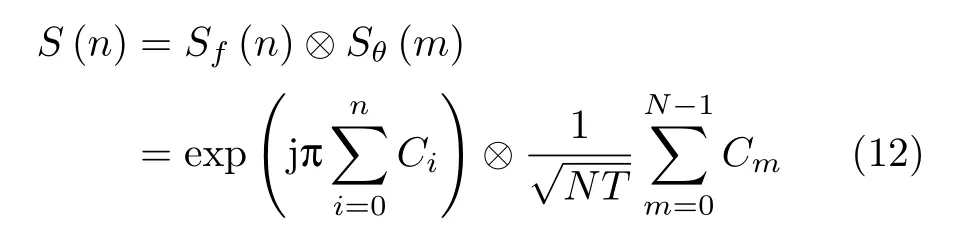
2 频谱特性
根据傅里叶变换特性,时域卷积相当于频域积相乘,可得到频谱为

Sf(f)的推导过程如下:
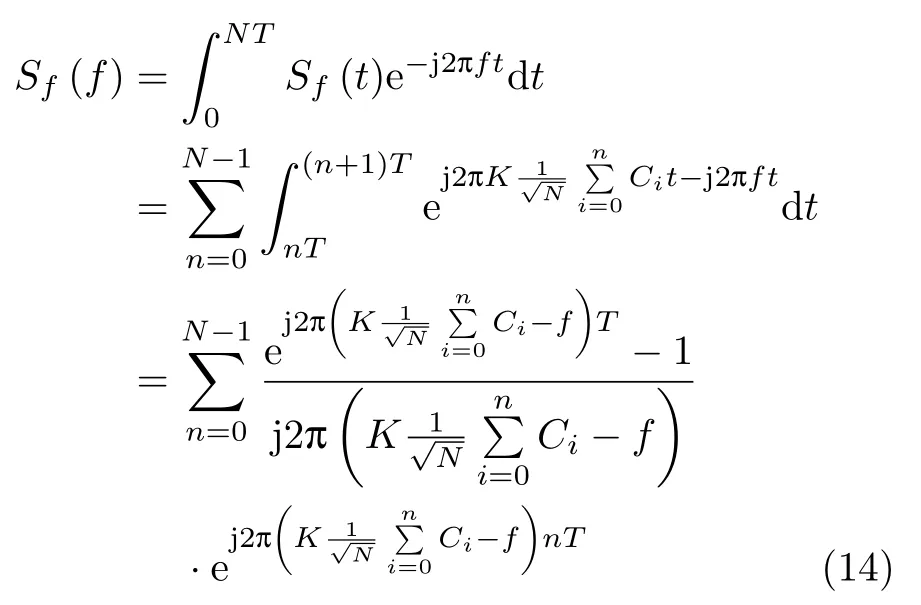
由欧拉公式可将式(14)进一步化简为

同样地,对Sθ(f)的推导过程为

把式(15)和(16)代入式(13),并取绝对值得到调频-相位信号波形频谱表达式

3 模糊特性
式(1)可进一步表示为

式中,0<t<NT,此时进行四相编码,即式中的d4(n)为ejn2π/M,n∈{0,1,2,3}.它的选择顺序与双混沌映射交叉混合编码得到的序列有关.
混沌序列具有随机性,各个子脉冲信号均不相同.因此,依据某个脉冲信号计算模糊函数具有一定的特殊性,不能准确反映复合混沌MIMO雷达信号的模糊特性.一种可能的方法是采用平均模糊函数来考察复合混沌MIMO雷达信号的模糊函数性能,本文选取在时间NT内进行计算
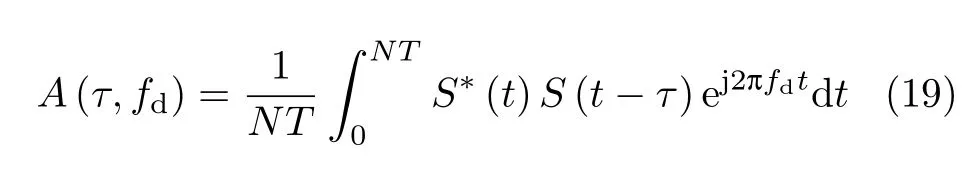
将式(18)代入式(19)可得

然后分别对积分区域(a,b)和(c,d)进行化简,得到的表达式如下:

当0<τ<T时,有n=m+1,此时a=n T+τ,b=(n+1)T,c=n T,d=n T+τ,则表达式为

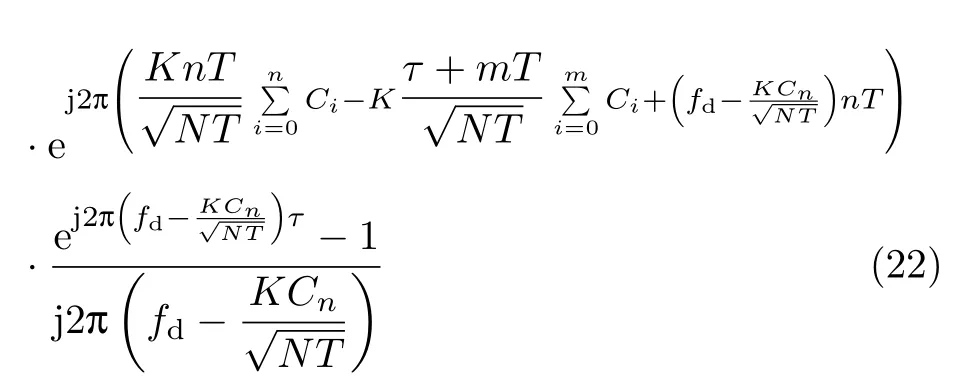
当τ>T时,为便于计算,采取qT<τ<(q+1)T,q=1,2,···,N-2,此时c=n T,d=(n-q)T+τ,n=1+m+q,则有
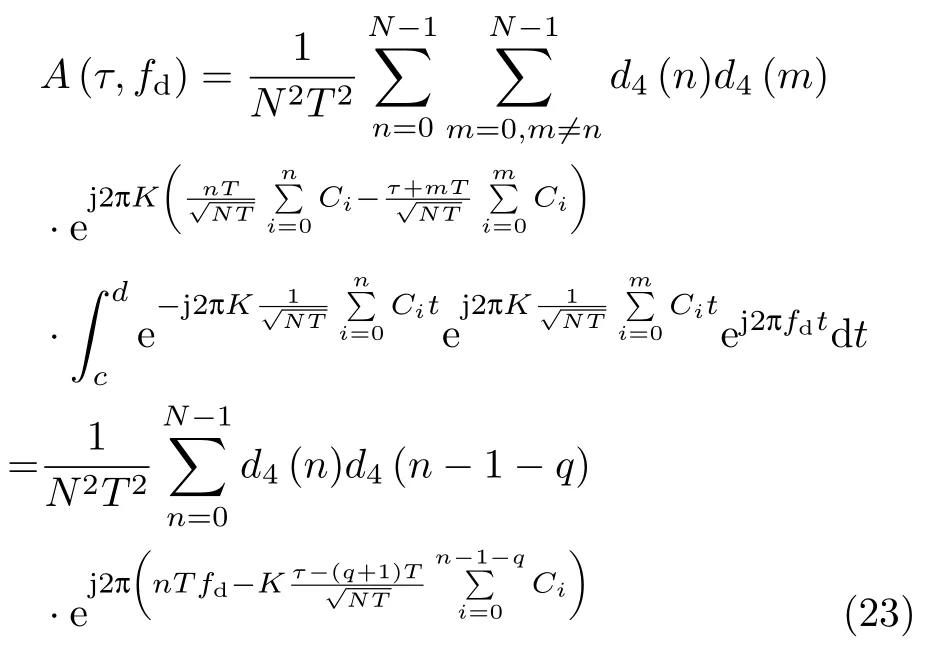
模糊函数是对称的,即|A(τ,fd)|=|A(-τ,-fd)|,从而得到完整的模糊函数A(τ,fd)的表达式.由式(22)和(23)可以看出:混沌调频-相位信号的模糊特性的表达式很复杂,那是因为混沌映射的表达式不确定.一旦确定混沌映射以及波形的设计方法,就可以得到比较确定的表达式.然后运用MATLAB软件绘制其模糊函数的图形.
4 信号波形相关性
本文假设MIMO雷达的信号波形数目为L,则信号离散形式的自相关函数和互相关函数[15]可用式(24)和(25)进行计算
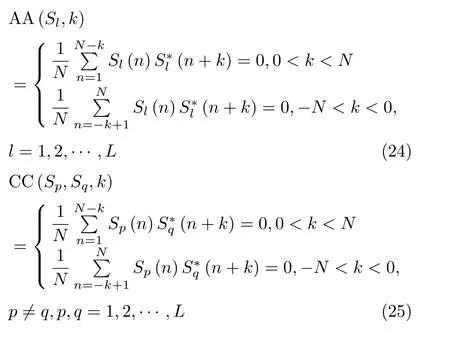
对于MIMO雷达正交信号,要求各信号之间互相关旁瓣峰值(CP)尽可能小,同时自相关旁瓣峰值(ASP)尽可能低,即应满足以下两个条件:

根据信号的模糊函数的定义,同时运用卷积公式可推导得到
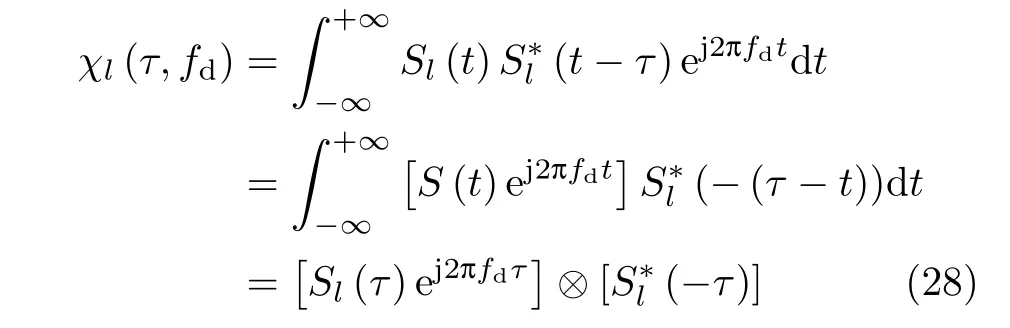
将Sl(t)=Sf(t)⊗Sθ(t)代入式(28)可得
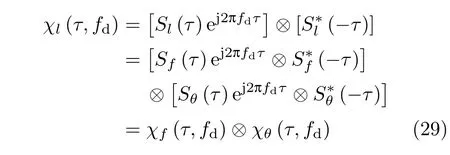
令fd=0,则有MIMO雷达的第l波形的自相关函数表达式
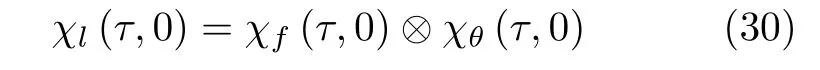
式中,χf(τ,0)可由式(28)计算得到,同时χθ(τ,0)亦为也可由式(28)计算得到,于是式(30)可进一步表示为

由式(31)可知,调频-调相的MIMO雷达的自相关特性是由调频的自相关特性和调相的自相关特性卷积后得到的结果,一旦确定混沌映射函数,就可以计算并绘出调频-调相的MIMO雷达信号波形集的相关特性图形.
5 波形设计方法
5.1 Bernouli,Logistic和Tent映射
Bernoulli映射产生的混沌序列可定义为xn+1=f(xn)=rxn(mod1),其中xn∈[0,1],r为大于等于2的整数.为实现一个抗干扰的高斯噪声,信号的改进形式为式中,wgn(1,1,p)为高斯白噪声,p为噪声强度.改进形式产生的序列在一定范围内是不可预测的,从而使系统被当作一个真随机比特源.离散时间混沌法不受其他噪声源的影响.
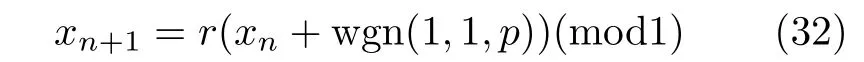
Logistic映射定义表达式为xn+1=βxn(1+xn),β∈[0,4],x∈[0,1],其改进形式为

Tent映射定义为xn+1=a-1-a|xn|,1≤a≤2,其改进形式为
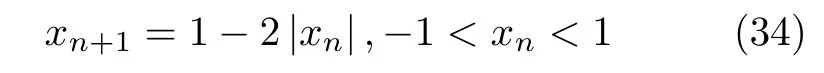
5.2 设计方法
假设MIMO雷达的波形数目为L,每个波形的子脉冲编码长度为L,相位数目为M,其具体步骤如下:
步骤1 在[0,1]之间随机选取L个初值,首先针对L个不同的初值,用Bernouli映射分别产生Ld个序列;然后将每个初值长度为Ld的混沌序列划分成Ld/N个长度为N的子序列;接着对这L个不同的初值,分别用Logistic序列和Tent序列产生长度为Ld/2个序列,同样地对不同初值的Logistic序列和Tent序列交叉混合,构成每个初值长度为Ld的混合混沌序列;同样分别将每个初值长度为Ld的混合混沌序列划分成Ld/N个长度为N的子序列.为了方便图形绘制,对产生的[-1,1]之间的混沌序列进行如式(35)的处理,使得到的序列范围在[0,1]之间,其中Ci为原始的序列,C′i为变换后得到的序列
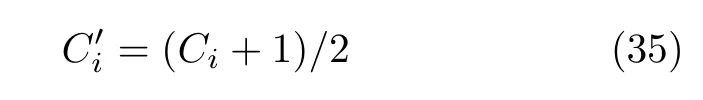
步骤2 将L个不同初值的Logistic序列和Tent序列交叉混合得到的序列进行式(10)的变换后再进行四相均匀量化,然后映射到相位编码信号波形上;同样将L个不同初值的Bernouli映射产生的序列进行变换后映射到调频信号上,从而得到了混沌映射的调频-调相的MIMO雷达正交波形集的离散复包络序列;
步骤3 对于L个不同初值,从每个初值得到的混沌调频-调相MIMO雷达正交波形集的离散复包络序列中选取一个自相关函数主旁瓣比最大的一个作为优选波形,得到L组混沌映射序列作为MIMO雷达正交波形.
6 计算机仿真实验
仿真参数设定如下:假设波形数目L=4,编码长度N=1 024,相位编码数目M=4,即采用四相编码,调制系数K=32 MHz/s,脉冲宽度T=4µs,采样频率fs=5 MHz.选取的初值分别为0.1,0.2,0.3,0.4,每个初值生成的初始序列长度Ld=10 240,Bernouli映射中噪声功率强度参数p=20d BW.本文采用Bernouli映射的改进形式xn+1=2(xn+wgn(1,1,p))(mod1)、Logistic映射的改进形式xn+1=1-2x2n、Tent映射xn+1=0.99-1.99|xn|来产生混沌序列.
实验1 频谱特性
图1为双混沌映射四相编码信号的频谱图,图2为单混沌加噪声Bernouli映射的调频编码信号的频谱图,图3为两者结合的混沌调频-调相编码信号的频谱图.从图1~3中可以看出,图3的频谱图更接近类噪声的频谱分布图,更具有随机性,不容易被敌方侦查到,而图1和2的频谱变化规律容易被识别,表明了两者结合的频谱图效果优于单个调制的效果.
实验2 模糊特性
模糊函数描述了目标的距离/多普勒频移产生的影响.由图4和5的等高线可以看出,模糊函数呈现理想的图钉状,且仅仅呈现单个峰值,即主要峰值区域在一个很窄的范围,因此能够获得很高的距离向和多普勒向的分辨率.图6为距离向的切片图,从图中可以看出分辨率类似一个冲击函数,亦表明其具有很高的分辨率.
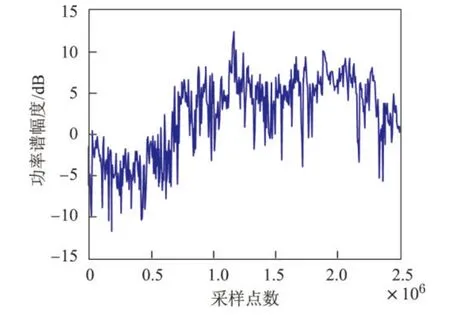
图1 四相编码信号的功率谱Figure 1 Power spectrum of four phase coded signal

图2 调频编码信号的功率谱Figure 2 Power spectrum of frequency modulation coded signal
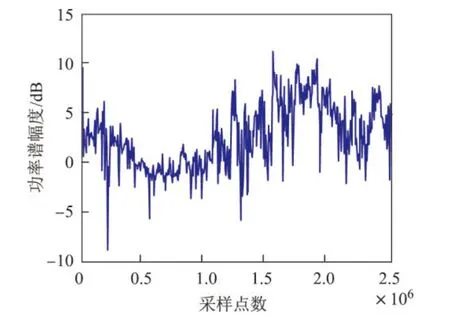
图3 调频-调相信号的功率谱Figure 3 Power spectrum of FM-phase modulation signal
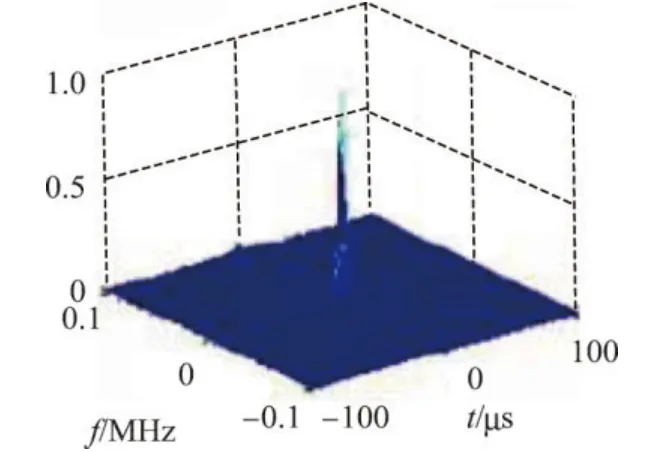
图4 模糊函数Figure 4 Ambiguity function
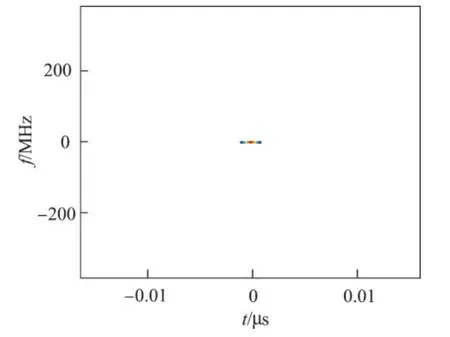
图5 模糊函数的等高线图形Figure 5 Contour map of ambiguity function

图6 模糊函数距离向切片Figur e 6 Distance slice of ambiguity function
实验3 正交性(相关性分析)
从图7和8中可以看出,自相关函数类似于冲击函数,互相关函数接近于零,表明混沌调频-调相编码波形集具有良好的正交性.由表1可以看出,在同样的波形数目和编码长度条件下,本文正交波形集的相关性优于文献[12]中的正交波形集,这主要得益于搜索空间的加大以及混沌映射方式的不同.
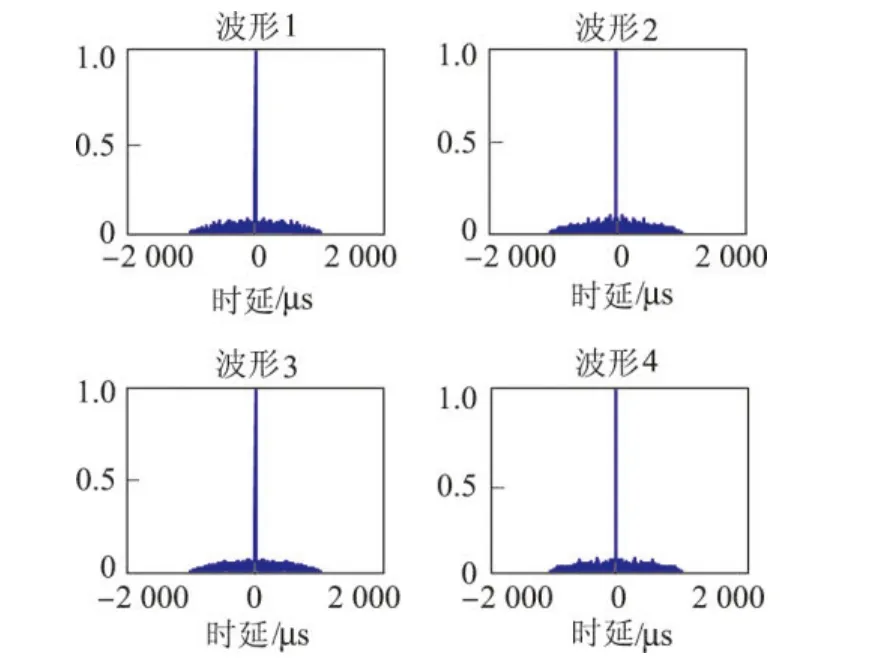
图7 自相关函数图形Figure 7 Autocorrelation function graph

图8 互相关函数图形Figure 8 Cross-correlation function graph
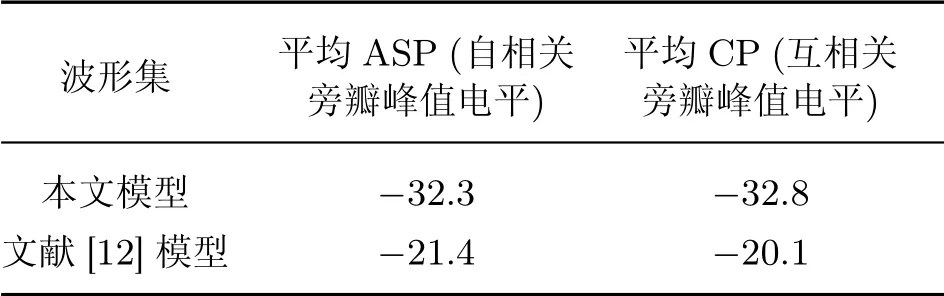
表1 计算值(L=4,N=1 024)Table 1 Calculation(L=4,N=1 024) d B
7 结语
本文提出了一种单双结合的混沌调频-调相MIMO雷达信号波形集.首先比较详细地分析并推导了离散化的表达式,然后对信号波形的频谱特性、模糊特性以及相关特性进行细致的推导和分析,最后进行数值仿真实验.仿真结果表明,相对于混沌调频以及混沌调相的MIMO雷达信号,单双结合的混沌调频-调相MIMO雷达的信号功率谱更具有随机性,更不易被敌方截获,其模糊函数的三维图形接近理想的图钉状,且比文献[12]具有更好的正交特性,从而说明单双结合的混沌调频-调相信号可以作为MIMO雷达信号波形集的一种很好的选择.
[1]徐爱辉.基于OFDM技术的低截获概率雷达体制研究[D].南京:南京理工大学,2012.
[2]WUXin,LIUWeixian,ZHAOLei.Chaotic phase code for radar pulse compression[C]//Radar Conference,2001.Proceedings of the 2001 IEEE,2001:279-283.
[3]LIUBo,HEZishu,ZENGJiankui.Polyphase orthogonal code design for MIMO radar systems[C]//Radar,2006.CIE'06.International Conference on IEEE,2006:1-4.
[4]孙成雨.MIMO雷达混沌相位编码信号设计与分析[J].电讯技术,2012,52(9):1497-1502.
SUNChengyu.MIMO radar chaosphase coded signal design and analysis[J].Telecommunications Technology,2012,52(9):1497-1502.(in Chinese)
[5]LIU Bo,HEZishu.Comments on discrete frequencycoding waveform design for netted radar systems[J].IEEE Signal Processing Letters,2008,15:449-451.
[6]牛超.基于两种映射的MIMO雷达混沌调频信号[J].现代防御技术,2012,40(5):121-125.
NIUChao.Based on two kinds of maps MIMO radar chaotic FM signal[J].Modern Defense Technology,2012,40(5):121-125.(in Chinese)
[7]李敬军,姜永华.但波.MIMO雷达中正交离散频率编码波形的设计[J].信号处理,2013,29(9):1177-1181.
LIJingjun,JIANGYonghua,DANBo.Orthogonal discrete frequency coding waveform design in the MIMO radar[J].Journal of Signal Processing,2013,29(9):1177-1181.(in Chinese)
[8]蒋飞,刘中,胡文.连续混沌调频雷达信号分析[J].电子与信息学报,2010,32(3):559-563.
JIANGFei,LIUZhong,HUWen.Analysis of the continuous chaotic based frequency modulated radar signal[J].Journal of Electronics&Information Technology,2010,32(3):559-563.(in Chinese)
[9]DENG Hai.Discrete frequency-coding waveform design for netted radar systems[J].Signal Processing Letters,IEEE,2004,11(2):179-182.
[10]张远安,张春荣,强勇.基于相位编码信号的MIMO雷达正交波形设计的研究[C]//2011年通信与信息技术新进展——第八届中国通信学会学术年会论文集,2011.
ZHANG Yuan'an,ZHANG Chunrong,QIANG Yong.Based on orthogonal phase coded signal of MIMO radar waveform design research[C]//New Progress in Communication and Information Technology,the Eighth China Communication to Learn Academic Essays,2011.(in Chinese)
[11]李明,郝明.基于混合遗传算法的正交相位编码波形设计[J].电子工程师,2007,33(10):1-4.
LI Ming,HAO Min.Waveform design of polyphase orthogonal code based on hybrid genetic algorithms[J].Electronic engineer,2007,33(10):1-4.(in Chinese)
[12]牛朝阳,李小波.MIMO雷达正交混沌调频波形集设计[J].信号处理,2013(3):394-399.
NIU Zhaoyang,LI Xiaobo.Design of orthogonal waveforms set for MIMO radar based on chaos frequency modulation[J].Journal of Signal Processing,2013,29(3):394-399.(in Chinese)
[13]ASHTARIA,THOMASG,KINSNERW.Sufficient condition for chaotic mapsto yield chaotic behavior after FM[J].IEEE Transactions on Aerospace and Electronic Systems,2008,44(3):1240-1248.
[14]刘嵩.MIMO雷达波形设计及参数估计研究[D].南京:南京理工大学,2013.
[15]申东,张林让,刘昕.基于混沌序列的MIMO雷达正交多相码波形设计[J].兰州大学学报:自然科学版,2011,47(1):100-105.
SHEN Dong,ZHANG Linrang,LIU Xin.Based on chaotic sequence is orthogonal polyphase codes of MIMO radar waveform design[J].Journal of Lanzhou University:Natural Science Edition,2011,47(1):100-105.(in Chinese)

