关于丢番图方程(45n)x+(28n)y=(53n)z的解

唐刚

(阿坝师范高等专科学校基础教育系, 四川 汶川 623000)

关于丢番图方程(45n)x+(28n)y=(53n)z的解

唐刚

(阿坝师范高等专科学校基础教育系, 四川 汶川 623000)

利用初等方法证明了,对于任意的正整数n, 丢翻图方程(45n)x+(28n)y=(53n)z仅有x=y=z=2正整数解.

丢翻图方程; 正整数解; 简单同余法; 分解因子法

1 引言

设a,b,c 为正整数, 且(a,b)=(b,c)=(a,c)=1,a2+b2=c2,则对任意的正整数n, 丢番图方程

显然有正整数解(x,y,z)=(2,2,2).

Sierpi'nski[1]证明了当n=1,(a,b,c)=(3,4,5), 方程(1) 仅有唯一的一组解(x,y,z)=(2,2,2)；Jes'manowicz[2]证明了当n = 1 且(a,b,c)=(5,12,13),(7,24,25),(9,40,41),(11,60,61)时方程(1) 仅有唯一的一组解(x,y,z)=(2,2,2),文献[2] 猜想对任意的正整数n 方程(1) 仅有正整数解(x,y,z)=(2,2,2),本文考虑了当(a,b,c)=(45,28,53)时, 方程(1)的解, 结论如下:

定理:对于任意的正整数n, 丢番图方程

有唯一正整数解(x,y,z)=(2,2,2).

2 引理

引理1设s≡3(mod4),t ≡2(mod4), 且s+t 含有某个4k-1型的素因子, 当n=1时, 则(1)仅有一组解(x,y,z)=(2,2,2)

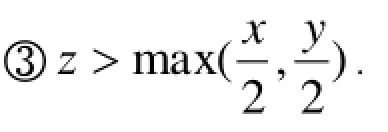
3 定理证明

由引理2可知,只需讨论max(x,y)＞z,且z＞2的情况

3.1 当n=1时

由引理1可知, 丢翻图方程成立45x+28y=53z有唯一正整数解(x,y,z)=(2,2,2).

[1] SIERPINSKIW. On the equation3x+4y=5z[J]. Wiadom M at, 1955, 56(1):194-195.

[2] JESMANOWICZ L. Several remarks on Pythagorean numbers[J]. Wiadom Mat, 1955, 56(1): 196-202.

[3] 乐茂华. 关于本原Pythagorean数组的Jes' manow icz猜想.[J]. 湖北民族学院学报: 自然科学版, 2008, 6: 121-122.

[4] 关文吉. 关于商高数的Je’smanowic猜想[J]. 纺织高校基础科学学报, 2011, 24(4): 557-559.

[5] 陆文端. 关于商高数组4n2-1; 4n; 4n2+1 [J]. 四川大学学报: 自然科学版, 1959, 2: 39-42.

On the Diophantine equation(45n)x+(28n)y=(53n)z

TANG Gang
(Department of Basic Education, Aba Teacher’s College, Wenchuan 623000, P.R.C.)

By the elementary method, this paper proves that, for any positive integer n, Diophantine equation(45n)x+(28n)y= (53n)zhas no solutions in positive integer other than x=y=z=2

Diophantine equation; positive integer solution; simple congruence; decomposition factor method

O156.7

A

1003-4271(2014)01-0101-04

10.3969/j.issn.1003-4271.2014.01.21

2013-10-24

唐刚(1980-), 男, 四川蓬安人, 讲师, 硕士, 研究方向: 数论、数学教育; E-mail: 30236243@qq.com.

阿坝师专科研基金项目(编号ASB11-10)