Banach格上AM-紧算子的M-和L-弱紧性
王雅娟, 陈滋利, 柳雅朋
(西南交通大学数学学院, 四川 成都 610031)
Banach格上AM-紧算子的M-和L-弱紧性
王雅娟, 陈滋利, 柳雅朋
(西南交通大学数学学院, 四川 成都 610031)
在Banach上对AM-紧算子与M-及L-弱紧算子之间的关系做了研究, 得到了当AM-紧算子是M-(L-)弱紧算子时, 其定义域和值域空间应具有的性质特征; 反过来也得到了M-(L-)弱紧算子在什么空间条件下是AM-紧算子的一些相关结论.
Banach格; AM-紧算子; M-弱紧算子; L-弱紧算子
1 引言
设E和F是Banach格,L(E,F)表示从E到F得所有有界线性算子组成的空间, 若有界线性算子T将E中序区间映为F中的相对紧集, 则T是AM-紧算子; 若有界线性算子T将E中闭单位球映为F中的L-弱紧集,则T是L-弱紧算子; 若有界线性算子T将E中的范数有界不交列映为F中的范数收敛于0, 则T是M-弱紧算子. 我们知道AM-紧算子不一定是M-(L-)弱紧算子, 如:Idc0:c0→c0是AM-紧算子但不是M-(L-)弱紧算子, 事实上c0空间具有序连续范数且是离散的,c0空间中的序区间是范数紧的, 所以Idc0:c0→c0是AM-紧算子, 容易验证Idc0:c0→c0不是M-(L-)弱紧算子; 及T:ℓ1→ℓ∞定义:

显然T是紧的, 则是AM-紧算子, 但不是M-弱紧算子(取{en}是ℓ1中自然基,{en}是范数有界不交列, T(en)=(1,1,1……)对∀n ),T也不是L-弱紧算子(取U是ℓ1中闭单位球,{en}是T(U)的实体包中不交列,不趋于0). 反过来, M-(L-)弱紧算子也不一定是AM-紧算子, 如: 自然嵌入J:L∞[0,1]→Lp[0,1]是M-弱紧算子但不是AM-紧算子. 关于M-(L-)弱紧算子与其他算子关系的研究已有很多结果, 主要有与半紧算子、Dunford-Pettis算子、几乎Dunford-Pettis算子、紧算子及弱紧算子之间的关系, 详见文献[4]、[6]、[7]、[8]、[9].
本文考虑M-(L-)弱紧算子与AM-紧算子之间的关系, 建立了AM-紧算子是M-(L-)弱紧算子的一些空间条件,同时对M-(L-)弱紧算子的AM-紧性也得到相关结论.
未经解释的有关Banach格和算子理论的一些概念、述语及符号详见文献[1][2][10].
2 AM-紧算子的M-弱紧性
设E是Riesz空间,0<e∈E, 若对每个x, 存在某个λ>0满足,则e称为E的序单位元. 若E有序单位e>0, 则Ee=E(Ee即由e生成的理想), 即E的闭单位球是序有界的, 因此也称范数有界与序有界是
等价的.
E是Banach格, 若E中每个弱收敛于0的序列都是范数收敛于0的那么称E具有Schur性质; 若E+中每个弱收敛于0的序列都范数收敛于0, 则称E具有正Schur性质; 当E中的每个使得xn↓0的序列{xn}都依范数收敛于0, 则E有序连续范数,E有Schur性质则E有正Schur性质(反过来不成立, 例:L1[0,1]),E有正Schur性质可以推出E有序连续范数.
下面我们看主要结论
命题2.1设E和F是Banach格,E有序单位, 则每个AM-紧算子T:E →F 都是M-弱紧算子.
证明:设{xn}是E中范数有界不交列, 因为E有序单位e, 则{xn}是序有界的, 又因为T是AM-紧算子,则T是序弱紧算子, 根据文[2]定理5.52, 所以即T为M-弱紧算子.
因为ℓ∞是有序单位的AM空间, 所以有以下推论.
推论2.2设E是Banach格, 每个AM-紧算子T:ℓ∞→E都是M-弱紧算子.
命题2.3设E和F是Banach格,E′有序连续范数且E有正Schur性质, 若T:E →F 是正则AM-紧算子,则T是M-弱紧算子.
证明: 设{xn}是E中范数有界不交列, 因为E′有序连续范数, 根据文[1]定理2.4.14, 则又E有正Schur性质, 根据文[4]定理3.1,(xn)相对弱紧集是几乎序有界的, 即对任意ε>0, 存在x∈E+, 有(xn)⊂[-x,x]+εBE, 从而

则T是M-弱紧算子.
注1: 若命题2.3条件只有E′有序连续范数, 则结论不成立, 例:Idc0:c0→c0是AM-紧算子,c0的共轭空间ℓ1有序连续范数, 但Idc0:c0→c0不是M-弱紧算子.
注2: 若命题2.3条件只有E有正Schur性质, 结论是不成立的, 例:Idℓ1:ℓ1→ℓ1是AM-紧算子,ℓ1有正Schur性质, 但Idℓ1:ℓ1→ℓ1不是M-弱紧算子.
命题2.3中E有正Schur性质得出(xn)相对弱紧集是几乎序有界的, 在定义半范数的基础上也可用得出.
设T是Banach格E到Banach空间X的线性算子, 我们定义E上的半范数qT如下(参看[1]):
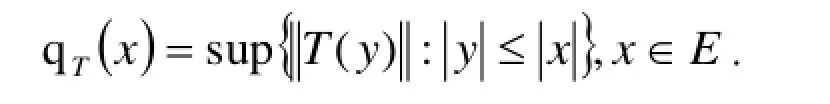
若T是几乎Dunford-Pettis算子, 则每个相对弱紧集关于半范数Tq是几乎序有界集. 由以上, 我们可得下面推论.
推论2.4设E和F是Banach格,E′有序连续范数且E中每个相对弱紧集关于半范数Tq是几乎序有界集,则每个正则AM-紧算子:TEF→都是M-弱紧的.
以上论证了AM-紧算子在一定条件下是M-弱紧算子, 那M-弱紧算子在什么情况下是AM-紧算子呢, 下面
研究M-弱紧算子的AM-紧性.
命题2.5设E和F是Banach格,E是离散且有序连续范数, 则每个正M-弱紧算子T:E→F都是AM-紧的.
证明:由已知, 根据文[2]定理2.3,E的格运算是弱序列连续的, 由文[6]定理2.3,T:E→F是Dunford-Pettis算子,又因为E有序连续范数, 根据文[5],T是AM-紧算子.
命题2.6设E和F是Banach格,F有Schur性质, 则每个M-弱紧算子T:E→F是AM-紧算子.
证明:设U是E中的序有界集, 且满足对任意的x∈U,V是F中闭单位球. 因为T:E→F是 M-弱紧算子, 根据文[2]定理5.60(1)有任意的ε>0, 存在u∈E+, 使得对任意的x∈U
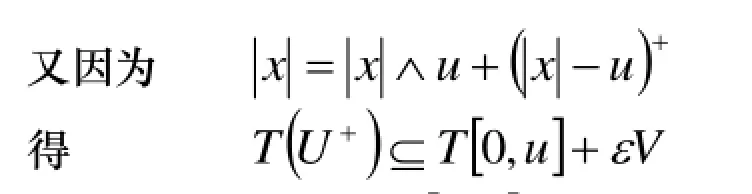
另一方面, 若{un}是[0,u]中不交列, 则因为T是M-弱紧算子有由文[2]定理5.52知T[0,u]是相对弱紧集,F有Schur性质, 所以得到T[0,u]是相对紧集, 根据文[2]定理3.1(4)知T(U+)是相对紧集, 所以T(U)是相对紧集,T是AM-紧算子.
3 AM-紧算子的L-弱紧性
E是Banach格,E中的非空集合A称为L-弱紧集当且仅当A的实体包里不交列都范数收敛于0; 所以T是L-弱紧算子有另一层定义, 即当T(U)实体包中的不交列都范数收敛于0(U为E中的闭单位球). 在有限维空间X中,U是E中闭单位球等价于U是E中范数紧集等价于U是E中L-弱紧集, 所以在有限维空间X中,任意有界线性算子都是L-弱紧算子.
命题3.1设E和F是Banach格,T:E→F是正则AM-紧算子. 若下列条件之一成立, 则T是L-弱紧算子.
(1)E有序单位,F有序连续范数.
(2)E′具有序连续范数,F′有序单位.
证明: (1)设U为E中闭单位球, 因为E有序单位, 则U为序有界集, 由已知T是AM-紧算子,T将序区间映射为范数紧集, 即T(U)是范数紧的, 又因为F有序连续范数, 根据文[13], 范数相对紧集一定是L-弱紧的,所以T(U)是L-弱紧集,T为L-弱紧算子.
(2)由已知T′:F′→E′, 因为E′有序连续范数, 根据文[1]命题3.7.23(i),T′是AM-紧算子. 又F′有序单位, 根据命题2.1,T′是M-弱紧算子, 由文[2]定理5.64,T是L-弱紧算子.
命题3.2设E和F是Banach格,E具有序单位,F有Schur性质,T是E到F的有界线性算子, 则T是AM-紧算子的充分必要条件是T是L-弱紧算子.
证明:必要性,F有Schur性质可以得出F具有序连续范数, 所以根据命题3.1得证.
充分性, 设x∈E+,[-x,x]是E中序区间, 所以是范数有界的, 则是E中闭单位球, 记为U, 则T(U)是L-弱紧集, L-弱紧集一定是相对弱紧的, 又因为F有Schur性质,T(U)是相对弱紧的, 即T是AM-紧算子.
注:F有序连续范数结论不成立, 例:T:ℓ∞→c0是L-弱紧算子, 但不是AM-紧算子.
[1] P MEYER-NIEBERG. Banach Lattices, Universitext[M]. Berlin :Springer-Verlag, 1991.
[2] C D ALIPRANTIS, O BURKINSHAW. Positive Operators[M]. New York: Academic Press,1985.
[3] A W WICKSTEAD. Converses for the Dodds-Fremlin and Kalton-Saab theorems[J]. Math Proc Camb Phil Soc, 1996 ,120:175-179.
[4] Z L CHEN, A W WICKSTEAD. L-weakly and M-weakly compact operators[J]. Indag Math, 1999,10(3): 321-336.
[5] B AQZZOUZ, L ZRAOILA. AM-compactness of positive Dunford-Pettis operators on Banach lattices[J]. Rendiconti del Circolo Matematico di Palemo, 2007: 305-316
[6] N CHENG, Z L CHEN,Y FENG. L-and M-weak compactness of positive Dunford-pettis operators[J]. Journal of Sichuan Nornual University, 2011, 34(5): 708-713.
[7] B AQZZOUZ, A ELBOUR, ANTHONY W WICKSTEAD. Compactness of L-weakly and M-weakly compact operators on Banach lattices[J]. Rend Circ, Math.Palerm, 2011, 60: 43-50.
[8] N CHENG, Z L CHEN,Y FENG. L-and M-weak compactness of positive semi-compact operators[J]. Rendiconti del Circolo Matematico di Palemo,2010, 59: 99-103.
[9] 李颖, 陈滋利. Banach格上几乎Dunford-pettis算子的M-弱紧性和L-弱紧性[J]. 西南民族大学学报:自然科学版, 2011: 37(4): 562-565.
[10] A C Zaanen. Riesz spaces II[M]. North Holland Publishing Company, 1983.
[11] B AQZZOU, R NOUIRA,L ZRAOILA. Semi-compactness of positive Dunford-Pettis operators on Banach Lattices[J]. Amer Math Soc, 2008, 136: 1997-2006.
[12] B AQZZOUZ, A ELBOUR. Some New Results on the Class of AM-Compact Operators[J]. Rendiconti del Circolo Matematico di Palemo, 2010, 59: 267-275.
[13] B AQZZOUZ, A ELBOUR, J HMICHANE. Some properties of the class of positive Dunford-Pettis operators[J]. J Math Anal Appl, 2009, 354: 295-300.
M- and L-weakly compactness of AM-compact operators on Banach lattices
WANG Ya-juan, CHEN Zi-li, LIU Ya-peng
(School of Mathematics, Southwest Jiaotong University, Chengdu 610031, P.R.C.)
This paper introduces and studies the relationship between the AM-compact operator and the M-(L-)weak compact operator, mainly focusing on the domains and range spaces for all AM-compact operator being M-(L-)weak compact operator. Some conclusions are obtained on how the M-(L-)weak compact operator is AM-compact operator.
Banach lattice; AM-compact operator; M-weak compact operator; L- weak compact operator
O153.1
A
1003-4271(2014)01-0079-04
10.3969/j.issn.1003-4271.2014.01.16
2013-10-28
王雅娟(1987-), 女, 硕士研究生, 研究方向:泛函分析; 陈滋利(1961-), 男, 教授, 博士生导师.

