模糊决策理论下的水利工程项目评标方法研究

吴庆林

模糊决策理论下的水利工程项目评标方法研究

吴庆林

(唐山市陡河水库管理处 河北唐山 063021)

以模糊决策理论为基础对水利工程评标，建立相应的模糊决策方法，对系统中的各因素进行识别判断，并进行适当的定量定性比较，决策结果会更加合理科学。本文结合工程实例剖析了模糊决策理论在水利工程中的应用。

模糊决策理论 水利工程 项目评标

目前我国水利水电工程业在全国推行了国际通行的工程建设招投标制度，水利工程项目招标投标率基本达100%。对水利工程评标的关键是选取合理的评标方法，只有客观、合理的评价方法，才能减少评标过程中的是非矛盾。我国多采用综合评价最优中标原则，主要考虑投标单位的报价、施工能力、管理水平、设备、经济状况、社会信誉等因素。这些因素大部分是一些模糊的概念，评标过程中很难把握，且评论结果受评论员自身的主观因素的影响也比较大。因素的模糊性导致评标过程和评标结果都具有一定程度的模糊性，以模糊决策理论为基础对水利工程评标，建立相应的模糊决策方法，对系统中的各因素进行识别判断，并进行适当的定量定性比较，决策结果会更加合理科学。

1 建立模糊决策模型指标体系

1.1确定评价对象的因素集和评价集

首先需判断建设工程的评价对象因素，主要为各级单位的投标文件，判断投标文件的质量水平因素即为评标指标体系，例如：技术表（U1）、商务标(U2)、社会信誉标(U3)等，评标对象因素集为U={U1，U2，U3}。确定评价集，对各项指标的满足程度设不同的评价等级，比如：

标价（U1）的评价集V={合理，较合理，一般，较差，不合理}

管理水平(U2)的评价集V={好，较好，一般，较差，差}

社会信誉(U3)评价集V={好，较好，一般，较差，差}。

1.2对各因素的单因素进行模糊评价

组织专家建立评价小组，本着完整性原则、非相容性原则、客观性原则、简洁性原则、规范性原则，对各投标单位的投标文件从商务标、技术标、社会信誉等方面，对评价的等级进行综合的判定分析，给出各评价等级的隶属度。专家评选的方法众多，但都要历经确定目标、建立指标预选集、筛选指标、确定指标体系这四步，具体见图1。

图1 评价流程图

2 评价指标体系

若投标方案有m个，考虑的评价因素有n个，那么第i个评价因素和第j个投标方案就用特征值xij表示，以此构建一个评价方案的特征值矩阵：

没有特征值的因素，由专家进行打分，并将此得分作为这个因素的“特征值”。每个评价因素的特征值的量纲允许不同，但量纲差异并不会影响到评价结果。个因素的指标特征值对于相应的评价指标来说，有些是越大越有优势（比如企业社会信誉、管理水平等），而有些则是越小越有优势（比如标价、施工工期），所以这两类特征值应当分开计算。

特征值越大越好型：

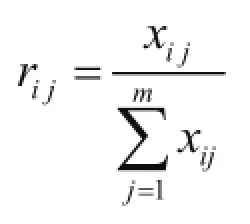
特征值越好越小型：

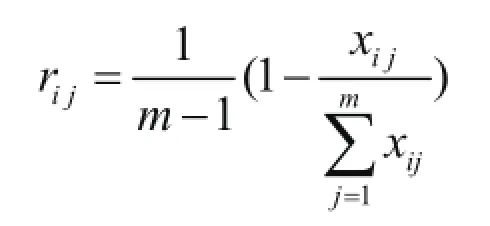
式中，ijr表示第j个方案第i个指标从属优的隶属度，上式可将指标特征值的矩阵转换成指标的隶属度矩阵：

3 确定权重，并对投标模糊综合评价

采用层次分析法确定权重，目前已在各个领域得到广泛应用。水利工程的评价要素较多，采用AHP层次分析法建立结构模型，两两比较，可以简化思维过程，使权重的确定更加科学。首先建立递阶层次结构，将各要素按照属性分为不同层次，上一层次的要素可对下一层次的元素起到支配作用，从上到下依次形成一个递阶层次性结构。值得注意的是，每一个层次结构的元素一般不得超过9个，层次结构的合理性对于分析结果的有效程度有很大影响。建立判断矩阵，所谓判断矩阵即是层次结构模型中同一个层次中每个要素相对它的上层要素，相互间做成对比较形成的矩阵。AHP法使得判断能够定量化，使用1～9标度，判定规则如表1所示。

通过比较得到判断矩阵A[aij]n*n求解计算矩阵，计算出最大特征根、特征向量，并作一致性检验。本文采用方根法求解，具体如下：

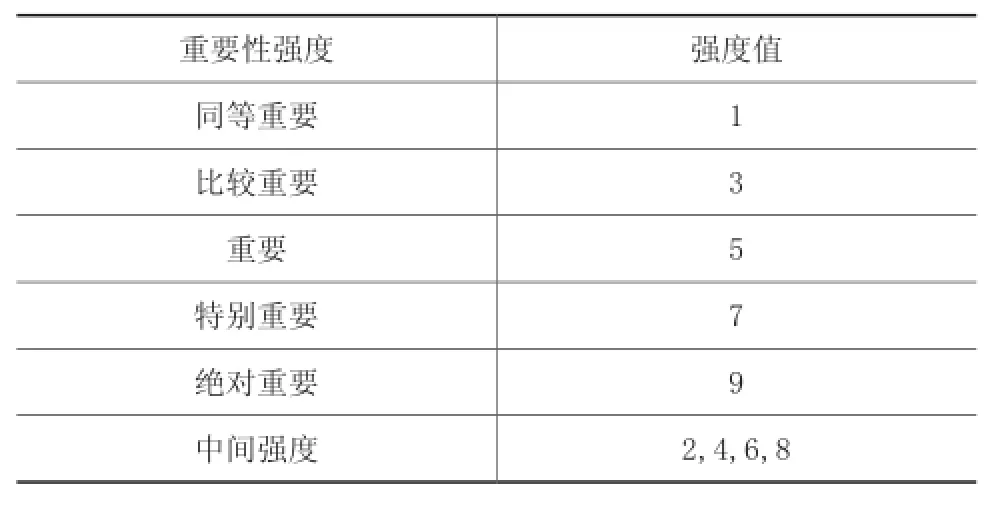
表1 重要性等级和强度值

（1）计算矩阵的单行各元素乘积，公式为：

（2）计算iM的n次方根，公式为：

（3）对iW−进行归一化处理，公式为：

（4）进行一致性检验，判断矩阵A要满足如下关系：

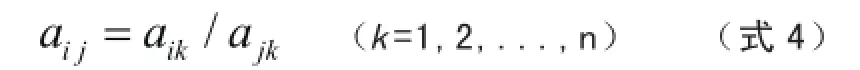
计算最大特征根maxλ：

计算一致性指标C.I.：

随机一致性比率C.R.：

R.I.可以查询表2可知。

判断矩阵需满足上述完全一致性的条件，有非零最大特征根，其余特征根为零。判断矩阵若不能满足完全一致性时，它的特征根也会改变。随机一致性比率小于0.1时，我们认为判读矩阵具备可以接受的一致性，上面所求的近似特征向量可以作为因子的权重，否则要调整矩阵直到满足条件为止。

表2 13阶平均随机一致性指标

4 实证分析

4.1工程概况

某一引水闸建设工程，标底4850万元，标底工期18个月，公开招标。经过预审和初评，共有6家施工单位进入详评阶段。

4.2建立评判指标体系、评价集

评价指标体系分三级，详细见图2。

图2 指标体系图

对本工程的指标评价集打分赋值，将所有的评价指标均分为五个等级，分别赋值为90,75,60,45,30。

4.3对各单因素进行模糊评价

采取三种评价方法针对不同的单因素进行评价。

（1）对于“U11总价”采取分布函数法进行评价，将六家投标单位分别编号为A、B、C、D、E、F，他们的投标总价分别为4700万元、4750万元、4900万元、5000万元、5100万元。浮动标底衡量法计算六家均价G1=4900万元，标底G2=4850万元，G1，G2的权重根据以往的经验定为：c=0.5,d=0.5，评标基准价为c*G1+d*G2=4875万元。用偏离度确定总价分值，偏差在-（5%～3%）得40分，-(3%～2%)得50分，-(2%～1%)得60分，-(l%～0%)得70分，+(0%～l%)得60分，+(l%～2%)得50分，+(2%～3%)得40分，+(3%～5%)得30分。经计算后得到6家公司的总价分值表，详见表3：

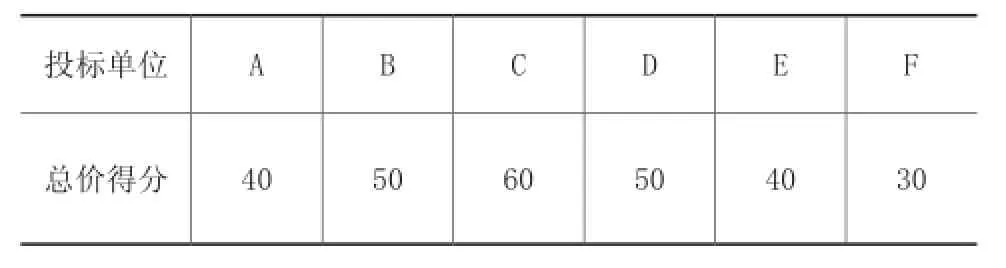
表3 总价得分表

（2）能够定性描述的指标采取模糊统计法，邀请10位专家对各公司的“U12”指标进行评价，得到模糊评判的结果，见表4.

表4 U12指标得分表

基于此构建特征值矩阵，再转化为隶属度矩阵R：

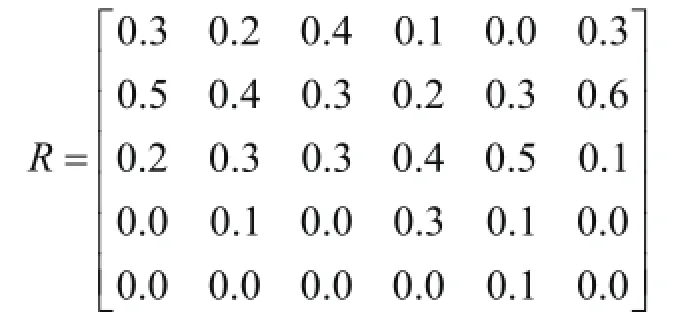
赋值向量A=[90,75,60,45,30]，U12模糊评判结果B：

其余的定性指标都按照相同的方法进行计算处理。

（3）对一些定量的指标采用评标因素特征值法进行评价，比如“U223”，该指标为提前竣工时间，水利工程由于其性质特殊往往不允许工期拖延。六家投标单位的提前竣工时间如表5所示。

TV11

B

1672-2469(2014)06-0041-03

10.3969/j.issn.1672-2469.2014.06.014

吴庆林（1970年—），男，高级工程师。