利用插值切割法研究重力区域场与局部场的分离

邢怡，滕菲，张国利

（中国地质调查局天津地质调查中心，天津 300170）

利用插值切割法研究重力区域场与局部场的分离

邢怡，滕菲，张国利

（中国地质调查局天津地质调查中心，天津 300170）

在重力数据处理中，将区域场与局部场相互分离是十分重要的，是反演解释的基础和前提。本文对插值切割法进行了改进，提出了全面插值切割法，并建立模型进行比较分析。结果表明新算法能在不失真的前提下减少振荡效应，加快算子收敛，提高处理速度，并能取得较好的分离效果。

插值切割；全面插值切割；局部场；区域场

在重力勘探中，数据处理是重要环节之一，也是进行重力反演解释的基础和前提[1]。将各种异常源产生的异常从观测到的实际数据中分离出来，是重力勘探方法取得良好地质效果的一条重要途径。因此，对重力异常分离方法进行研究，具有理论意义和实用价值。

通常将重力实测数据看作区域场与局部场的组合，如何将二者准确的划分，目前尚无公认的通用方法。常见的趋势面分析法、匹配滤波法及向上延拓等方法，在划分不同深度层次的局部场与区域场时，都有一定的局限性，很难取得令人满意的效果。与它们相比，插值切割法具有畸变小、划分精度高的优点，并且有很好的收敛性，所以近几年此方法被普遍关注。

1 基本原理

插值切割法[2]是以程方道等[3]提出的多次切割法为基础转变而来的，汪炳柱等[4]和段本春等[5]应用插值切割法解释油田的磁异常取得了一定的效果。本文对其算法进行改进，可进一步压制区域场振荡效应，加快收敛，提高处理速度，其算法原理如下：

设测区D内重力测量G(x,y)由区域场R(x,y)和局部场L(x,y)组成，即

将原插值切割法算子A(x,y)由4点圆周平均值改为8点窗口平均值，即

式中，a和b是加权系数，a≥0,b≥0，且a+b=1。

对于加权系数的确定，改由下列算法求取：

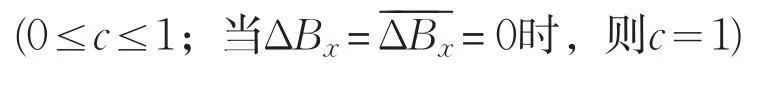
用上述方法得到的区域场称为第1次切割的区域场，用R1(x,y)表示；对R1(x,y)重复使用以上方法，得到第2次切割的区域场R2(x,y)；依次迭代下去，最终有:

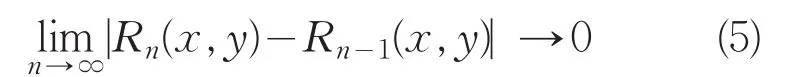
于是有

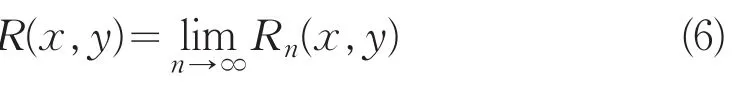
称这个区域场Rn(x,y)为切割半径r的区域场。一般在实际计算时，将公式(5)改成下面的不等式

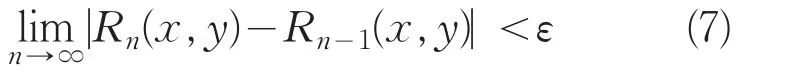
不等式中ε为切割精度，取ε为一个很小的正数。当不等式成立时，就结束迭代运算。将重力测量G(x,y)与区域场Rn(x,y)相减，得到局部场：

根据原理可知，一般切割半径r越大，切割出的局部场所反映的空间尺度就越大。此外，为了尽量减少数据边部损失，插值切割前还需要对数据进行扩边处理[6]。

2 误差传递规律

实测数据中不可避免地存在一定的观测误差，尤其是随机误差。因此，在插值切割中会产生误差传递，由误差传递公式可以推出原算法的均方误差传递关系[2][7]为：

由于各点的均方误差相同，设为δ0，误差传递系数Kn=(δ/δ0)n，式中n为误差传递的次数，则求得n次插值切割后，误差传递系数为(5/5)n≤Kn≤1。对于改进算法的均方误差传递关系为：

求得误差传递系数为(1/3)n≤Kn≤1。通过分析可以得出：改进后算法不会使随机误差放大，而且还比原算法加快了收敛，提高了数据处理的速度。

3 模型验证

建立一个由两个球体组成的地质模型，模型结构如图1所示。其中两球体的密度都为2 kg/m3，D=500 m，R=200 m，h=10 m，r=8 m，对应的等值线见图2。为了能找出切割半径r与切割精度ε的选取规律，我们选取不同的切割半径r与切割精度ε，对模型等值线数据进行插值切割分离，并且统计出针对模型不同切割半径r与切割精度ε的误差，详见表1。其中，标记处是切割误差最小时对应的切割半径与切割精度。

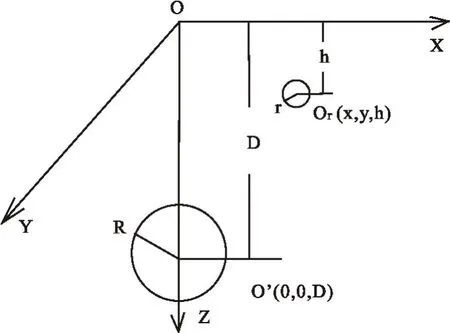
图1 两球体组成的模型Fig.1 The two sphere model

从表中可以看出，并不是切割半径越小，切割精度越高，得到的切割效果就越好。当切割精度一定时，选取的切割半径过大或过小，均会带来较大误差，切割效果不理想。当切割半径一定时，误差的减小不能单靠提高精度来解决，精度太高会使区域场失真，因此处理时要选择合适的精度。

在最小误差条件下，用原算法处理模型数据，程序迭代126次，用时0.811秒；用改进算法，程序迭代18次，用时0.234秒，处理结果如图3、图4所示。可以明显地看到，改进的算法使区域场振荡效应得到了明显压制，局部场更接近于模型。

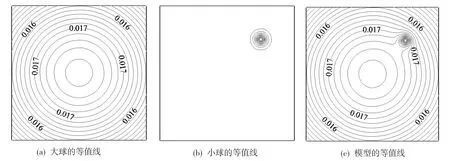
图2 两球体模型的重力正演图Fig.2 The gravity forward map of two sphere model

表1 两种插值切割法的误差统计Table 1 Two interpolating cut method of error statistics

图3 插值切割法的等值线图Fig.3 The contour map of interpolating cut method

4 结语

本文对原有插值切割法进行了改进，将原插值切割法算子由4点圆周平均值改为8点窗口平均值，提出了全面插值切割法。通过以上讨论，可以看出新算法能加快算子收敛，得到更好的分离效果。划分出的局部场畸变较小，区域场振荡效应有所减小，处理速度得到提高。

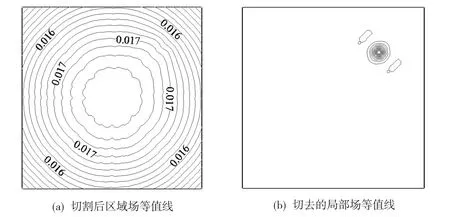
图4 改进插值切割法的等值线图Fig.4 Contour map of all interpolating cut method

[1]罗孝宽，郭绍雍.应用地球物理教程—重力磁法[M].北京：地质出版社，1991.

[2]文百红，程方道.用于划分磁异常场的新方法—插值切割法[J].中南矿冶学院学报，1990，21(3)：229-235.

[3]程方道，刘东甲，姚汝信.划分重力区域场与局部场的研究[J].物化探计算技术，1987，9(1)：1-9.

[4]汪炳柱，徐世浙，刘保华，等.多次插值切割法分场的一个实例[J].石油地球物理勘探，1997，32(3)：431-438.

[5]段本春，范典高.利用插值切割法研究磁性基底局部起伏特征[J].石油物探，1999，38(4)：89-95.

[6]段本春，徐世浙.磁(重力)异常局部场与区域场分离处理中的扩边方法研究[J].物探化探计算技术，1997，19(4)：298-304.

[7]刘东甲，程方道.划分重力区域场与局部场的多次切割法[J].物探化探计算技术，1997，19(1)：31-35.

[8]徐世浙，张研，文百红，等.切割法在陆东地区磁异常解释中的应用[J].石油物探，2006，45(3)：316-318.

[9]秦葆瑚.用分层切割法研究复杂磁异常[J].物探化探计算技术，1994，16(2)：96-101.

An Interpolating Cut Method for Separation of Regional and Local Gravity Field

XING Yi,TENG Fei,ZHANG Guo-li
（Tianjin Center,China Geological Survey,Tianjin,300170,China）

Data processing is an important step in the gravity exploration.In this working process,it is important to separate regional and local field,because it is the base of inversion explanation.We succeed in improving the interpolating cut method,and establish models to compare the two methods.Due to the improvement,we can get higher precision,faster calculating speed and fewer distortions.

interpolating cut method;all interpolating cut method;local field;regional field

P631.1+2

A

1672－4135（2014）03－0193-04

2014-0614

中国地质调查项目：区域地球物理调查成果集成与方法技术研究（1212011120915）

邢怡（1983-），硕士，工程师，2008年毕业于中国地质大学（北京）地球物理与信息技术专业，E-mail:xingyi_ 83@sohu.com。