多种地球化学异常下限确定方法的对比研究

陈健，李正栋，钟皓，武明贵

（青海省有色地质矿产勘查局地质矿产勘查院，青海西宁 810007）

多种地球化学异常下限确定方法的对比研究

陈健，李正栋，钟皓，武明贵

（青海省有色地质矿产勘查局地质矿产勘查院，青海西宁 810007）

地球化学异常下限值是区分背景区与异常区的基本参数，而异常下限的准确性直接关系到下一步找矿工作的实施。本文以青海省治多县区域1∶1万土壤化探样品中Ag、Cu、Zn、Pb、Bi、Mo、W七种元素为例，使用传统计算方法、85%累计频率法、分形方法对测试数据进行处理，对比研究认为：传统计算方法求得的异常范围小，且较为分散；85%累计频率法与传统方法所得异常下限值比较接近，具有合理性与客观性，相对于传统计算方法，分形方法对弱小异常的识别效果显著，但异常范围过大，给异常查证工作带来难度。确定异常下限值时要研究数据分布模式和地质背景，分析区域地球化学特征差异，应采用多种分析法对比确定合理的异常下限，圈定出有效的异常区。

地球化学异常；异常下限；分形方法；85%累计频率法；青海省

确定地球化学异常下限是勘查地球化学工作中的一个基本问题，也是勘查地球化学应用于矿产资源勘查工程中指导成矿远景评价的一个关键性环节[1]。确定的异常下限过高，易遗漏隐伏矿床形成的矿致异常，而异常下限过低，容易干扰矿致异常的识别和弱异常的提取。但由于区域地质背景和成岩、成矿作用的复杂多样，迄今仍没有发现一种普遍适用的异常下限的计算方法，各种方法各有优势，同时又存在假设条件的制约和使用的局限性。因此，在生产与科研工作过程中，采取多种方法计算，并结合区域地质背景进行综合对比研究来确定异常下限，是能够圈定合理异常区的一种有效途径。

1 研究区地质背景概况

研究区位于可可西里－金沙江缝合带与乌兰乌拉湖－玉树断裂之间，呈北西西向分布。区域地层以中生代地层为主，有三叠纪巴颜喀拉山群、巴塘群、结扎群，侏罗纪雁石坪群，白垩纪风火山群,以及分布较局限的第四纪沉积地层。对成矿有利的地层主要是二叠纪、三叠纪地层。广布的上三叠统以钙碱性火山岩为主，间有浊积岩及碳酸盐岩沉积，通称为巴塘群，岩性以流纹岩、英安岩、安山岩为主，另有少量玄武岩、玄武质粗安岩，均为钙碱性系列，其岩石地球化学等各方面的特征反映构造环境与岛弧或活动大陆边缘颇为相似，并与俯冲作用有关[2]。

区内构造线展布方向为北西－南东向，处于北西、北东、东西三组构造带的交汇部位，构造环境十分复杂。区内经历了长期复杂的构造运动，断裂构造和褶皱构造相当发育；按其展布方向可分为北西向、北东向、近东西向三组断裂，各断裂彼此交错切割，共同构成区内基本构造轮廓；北西西向和北西向两组断裂为测区内的主要断裂，在断层附近形成较宽的挤压破碎带。

区内岩浆活动强烈，侵入岩不发育，火山岩分布广泛，其展布受区域构造的控制。区域岩浆活动主要以喜山期中酸性侵入岩为主，次有少量燕山期中酸性火山岩。喷出活动主要集中于晚三叠世和新近纪。前者为海相裂隙喷发岩，呈层状，主要为酸性-中性-基性熔岩与火山碎屑岩，岩性为安山岩、凝灰岩、安山玄武岩、火山角砾岩、流纹岩等，是巴塘群重要构成。后者火山岩由流纹岩、安山岩、火山角砾岩及少量凝灰岩、安山玄武岩、粗面安山岩组成。

2 区域地球化学特征

研究区属半湿润－草甸区，位于西金乌兰－玉树地球化学成矿区。对一些低弱的Cu异常（地表Cu

弱矿化地段），应运用探槽、浅钻等手段采集较深部样品，分析其元素的含量，以便对异常作进一步的解释与评价。巴塘群岩石微量元素地球化学特征显示，在碎屑岩中粒度越细铜含量越高,变质越深铜含量也越高。安山岩与石英安山岩中铜、铅含量较高。玄武岩中银含量偏高。西金乌兰－玉树地球化学成矿区是Cr、Ni、Ti、Cu、Zn、Ag、Cd等元素高含量、高背景地区，U、Sn、Bi等元素在矿带内呈低背景、低含量分布。在区内还有Cr、Ni、Cu、Au及U、稀土异常存在，但规模相对逊色，有的可能为岩性异常[4]。邻近的沱沱河－杂多地球化学区也是Cu、Mo、Pb、Zn、Ag、Hg等元素呈高背景、高含量分布，Au、Ba等元素在矿带内呈低背景、低含量分布，其中Mo、Pb、Zn、Ag、Cd的均含量居青海省其他地区。区域化探异常元素组合和分布存在南北差别是该区地球化学的又一显著特点[4]。因此，成矿元素有着良好的成矿背景高值域，容易形成Pb＋Zn＋Cu等金属矿床(表1)。本次1:1万土壤化探工作布设网度为100×40 m2。中国北方土壤化学元素均值参照《应用地球化学元素丰度数据手册》[5]。

3 地球化学异常下限的确定方法

3.1 传统计算方法

传统计算方法是建立在数据符合正态或对数正态分布基础上，但在实际工作中没有任何数据完全服从正态分布。对于测试数据一般要对所取得的化探数据进行常规的数据处理，即离群点数据(最高值、最低值)的迭代处理，一般采用大于X＋3S的异常值剔除，小于X-3S的异常值剔除（注：X-平均值；S-均方差），直至无离群点数值可剔除为止，使其符合正态分布，即所有数据全部分布在X-3S与X＋3S之间，即形成背景数据，再以背景值加2倍均方差（X＋2S）计算出异常下限（表2）。

3.2 85%累计频率法

累计频率就是一个数值的频率和比它的频率高的数值频率的总和。设x1＜x2＜…＜xm是不重复的样本值，m＜n。把样本值小于或等于个样本的数据xi的频率累加，得到小于或等于xi的累积频率。再把累积频率85%时的xi值作为异常下限（表2）。

3.3 分形理论方法

由于化探异常的复杂性，且随着地表矿化信息的减少，找矿重点向寻找隐伏矿和深部矿方向发展，一些新的化探异常筛选评价方法不断涌现，如分形理论已应用到地球化学领域，分形理论在化探数据处理中的应用主要在异常下限的确定方面。目前利用分形理论进行地球化学异常下限确定的方法主要有含量－面积法、含量－距离法、含量－个数法、含量－频数法、浓度－面积法等。其中，应用比较广泛的是含量－面积法和含量－频数法。孟宪国等[8]研究表明,地质数据中广泛存在分形结构；刘二永等[3]用分形技术进行化探异常查证；成秋明等[9]研究了地球化学异常，并用分形方法区分地球化学背景值，取得了较好的效果；Goncalesm[10]提出用二维多重分形方法模拟集中的重新分配地球化学数据；申维等[11]提出了多维自仿射分形与分布的概念，并将分形和多重分形建模应用于区域地球化学元素数据中。

表1 元素测试数据均值与元素丰度比较（10-6）Table 1 The average value of the test data and elemental abundance（10-6）

表2 不同方法确定的异常下限值对比（10-6）Table 2 Geochemical anomaly lower limit values from the three methods（10-6）

分形分布的特点要求大于某一尺度物体的数目，与物体大小之间存在幂函数关系。设分形模型[8-12]为：

其中，r表示特征尺度；C＞0称为比例常数，D＞0称为一般分维数[12]；N(r)=N(≥r)表示尺度大于等于r的数目或和数。例如r可表示元素含量，N(≥r)表示元素含量大于等于r的样品数目或和数。分形分布可以应用于那些具有标度不变性的地质现象，而标度不变性则提供了应用分形分布的基础。

设地球化学元素值{xi},i=1,2,…,N。

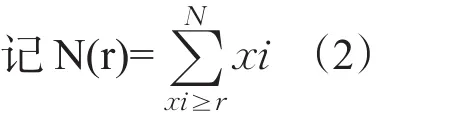
式(2)是对于所有满足xi≥r的i求和，minxi≤r≤maxxi。这样得到了数据集(N(ri),ri)(i=1,2,…,n＜N)。将这些数据代入式(1)，两边取对数，将它化为一元线性回归模型[13-15]：

用最小二乘法求出斜率D的估计量，即为分维数；当其散点大致分布在二段直线上时(即分二组的情形)，可采用分段拟合，有的界限点清楚，有的则不清楚。为了提高界限点确定的客观性，在二个区间用最小二乘法进行回归时，用了最优化方法来确定界限点。其基本方法：找出合适的界限点ri0（分形下限）,使各区间拟合的直线与原始数据点之间的剩余平方和Ei(i=1,2)在二个区间的总和为最小。

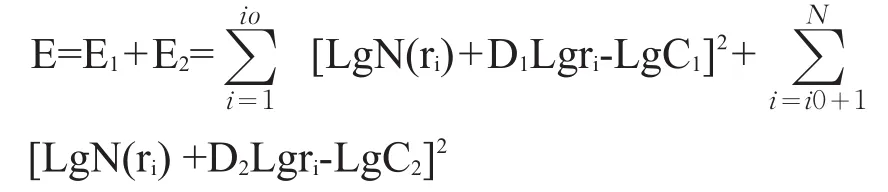
其中，ri是元素含量，D1和D2分别为相应区间的斜率，即分维数。检验回归方程的显著，要求对每个回归方程都进行了相关系数检验及方差分析检验。求得的异常下限见表2。图1、图2为研究区土壤中Ag、Cu元素含量－频数关系。

应用测试数据，在Lgr-LgN(r)坐标中投点（图1），用最小二乘法得到相应的直线方程：

得到分维数D1=0.2201，D2=2.1221，界限点ri0(分形下限)=76.4×10-9。以上方程均通过显著性检验。应用测试数据，在Lgr-LgN(r)坐标中投点（图2），用最小二乘法得到相应的直线方程：

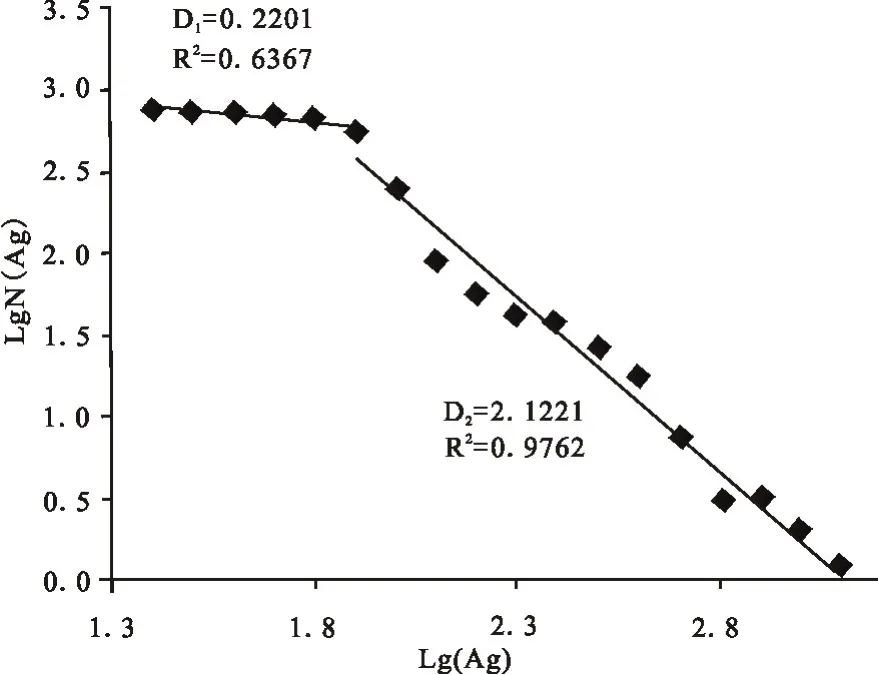
图1 研究区土壤中Ag元素含量-频数关系Fig.1 The content-frequency relationship of soil Ag in study area

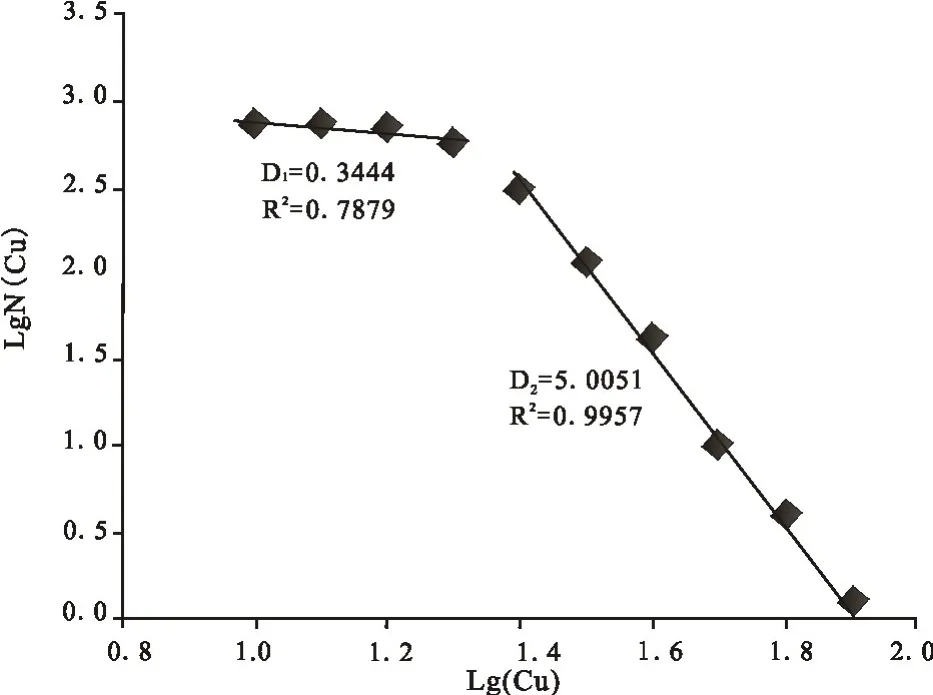
图2 研究区土壤中Cu元素含量-频数关系Fig.2 The content-frequency relationship of soil Cu in study area

得到分维数D1=0.3444，D2=5.005，界限点ri0(分形下限)=26×10-6。以上方程均通过显著性检验。

4 分析结果与讨论

本文分别用传统计算方法、85%累计频率法和分形理论方法，对元素含量数据进行处理，求得异常下限。表2列出了不同方法确定的异常下限结果。

从表2中可以看出，三种异常下限计算方法得到

结果的差异很明显，异常下限值总体上呈现的规律：传统计算方法确定的异常下限值＞85%累计频率法确定的异常下限值＞分形理论方法确定的异常下限值，由此推知异常区的圈定范围大致为：传统计算方法圈定的面积＜85%累计频率法圈定的面积＜分形理论方法圈定的面积。各元素在用传统计算法、85%累计频率法和分形方法得到的异常下限没有规律性，这与元素含量数据的分布特征及异常下限计算方法密切相关。地球化学场元素的分布形式可分为两类：正态和多模式分布、分形和多重分形分布，正态和多模式分布对应混合作用占主导地位的地球化学过程，而分形和多重分形分布对应分异作用占主导地位的地球化学过程［16］。

通过异常下限计算，对比传统统计法、85%累计频率法和分形理论方法，可以得出：Ag、Cu、Zn、Pb四种元素分形方法确定的异常下限明显低于传统方法确定的异常下限，其他元素的异常下限虽有偏差则不是很大。造成这种偏差较大的主要原因：

（1）测区内地球化学数据不严格服从正态或对数正态分布，基于正态分布的异常下限计算缺乏理论基础[17]；基于地球化学数据结构的分形理论具有完整的理论基础。

（2）分形方法计算异常下限时不损地球化学数据的完整性，而传统的对数异常下限的计算方法均经过数据剔除。

在实际生产与科研工作中，对数据总体分布有充分的判定且可确定其分布类型时，传统统计方法更具有针对性，有效性，首先要剔除离群点数据（＞X+3S与＜X－3S）至使数据服从正态分布，确定出的异常下限值并非由全部数据而只是由背景值决定，这种方法对判定小区域值效果较好。85%累计频率法则充分利用了研究区的全部数据信息，将研究区15%的数据作为异常数据来评价。分形理论在确定异常下限的过程中也充分利用了所有测量数据，一般分为两段，不像传统计算方法的只是一个数值。矿化元素的富集，受到多期次地质构造活动和成矿作用的控制，反映在地球化学元素含量数据上，其分布特征均表现为不服从正态或对数正态分布，而是呈多峰态、高丛集的多重分形分布特征。分形方法的理论依据是，地球化学场具有分形结构，由于背景场和异常场的主要控制因素不同，而形成多个区间的分形分布，低分维数的分形分布对应地球化学背景，高分维数的分形分布对应于地球化学浓集分带。采用分形法对研究区地球化学场特征进行分析，可以很好地揭示各主要异常空间变化及元素富集规律。从方法原理看，多重分形法和85%累计频率法利用了所有测量数据，所计算的异常下限值具有合理性与客观性，分形法圈定的异常有效合理，是一种方便快捷、值得推广的化探数据处理方法。

从本研究区来看，多重分形法和累计频率法确定的异常下限相对于其他方法较低，一定程度上也是该地质单元的地球化学背景的反映，给异常查证工作带来困难。综合各个元素三种异常下限对比及地质构造分析，研究区采用分形理论方法确定异常下限更合理。不同元素使用不同方法确定的异常下限值不同，某一方法对于某种元素而言，确定的异常下限值是最低的，能将一些弱异常反映出来，同时也会给异常查证工作带来难度[18]。在分布有多个地质单元的地区开展化探工作时，要考虑不同地质单元的地球化学背景差异，不能在全区采用统一的异常下限，如采用归一化法、数据滤波处理法和按地质体背景圈定等方法确定异常下限，进行对比分析，确定出一种能够更好地反映出异常分布空间特征和元素富集变化规律的方法。因此，在实际工作中确定异常下限首先要考虑测试数据的分布模式，其次要与实际地质背景相结合，充分研究数据分布模式和地质背景的基础上，才能确定使用哪种计算方法更合理。

为了更好地比较三种异常下限的确定方法的客观性和适用性，笔者在此将Ag、Cu两元素按三种不同异常下限通过MAPGIS6.7软件勾画出异常图（图3）。由图4可以看出，圈出的地球化学异常差异比较大。①分别应用分形方法确定的异常下限（分形下限）和85%累计频率法确定的异常下限圈定的异常范围比用传统方法确定的异常下限（算术下限）圈出的异常范围要大，避免了遗漏有用的矿化信息，也提取出一些弱异常信息。而使用传统方法确定的异常下限容易漏掉一些已知矿体的信息。②应用分形方法圈定的异常区将已知矿化点几乎全部包含在内，而用传统方法圈出的异常区只包含少量已知的矿化点。因此用分形方法获得的结果与实际勘查结果吻合程度较高，反映了实际的异常范围。③分形方法确定的异常下限（分形下限）和85%累计频率法，异常套和较好，能够指示有利的找矿信息。

综上所述，可推测在研究区西北部与南部存在

铜矿床的可能性较大（即现今没有发现铜矿化点），即图4的左上角区域和右下角区域，今后应注重该区域的详细勘查工作。

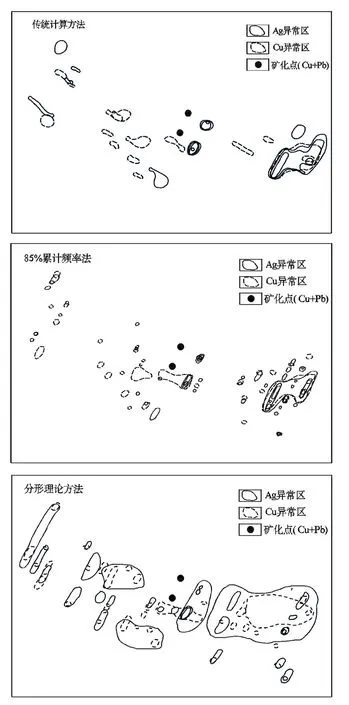
图3 Ag、Cu两种元素组合异常对比图Fig.3 Comparison among Ag and Cu element combination anomaly in the work area

5 结论

（1）三种方法确定的异常下限之间有差异，原因在于：传统方法要剔除离群点数据，异常下限值并非由全部数据而只是由背景值决定，该方法对判定一般值效果较好。而分形方法是基于测试数据的变化特征与结构，利用所有测试数据，低分维数的分形分布对应地球化学背景，高分维数的分形分布对应于地球化学浓集分带，能够揭示异常空间变化及元素富集规律，是一种实用快捷、值得推广的化探数据处理方法。85%累计频率法同样也是利用所有测试数据，其计算的异常下限也具有合理性与客观性。

（2）分形方法圈出的Ag、Cu下限异常区与实际已知Ag、Cu矿化点吻合情况较好，同时能将一些弱异常反映出来，但也给异常查证工作带来一定的难度，这可能是方法局限性的表现，科学的方法是既能圈出低背景区的弱异常，也能够避免高背景区划大异常或划出非矿致异常。而传统计方法圈定的异常区易漏掉了一些矿化指示信息。

（3）在科研生产工作中，要研究数据分布模式和地质背景，分析区域地球化学特征差异，应采用多种分析法对比确定异常下限值更合理。

（4）研究认为研究区西北部与南部存在铜矿床的可能性较大，为下一步找矿工作指明了方向。

[1]李蒙文,赵明国,赵财胜.稳健估计方法在内蒙古新忽热地区水系沉积物测量异常评价中的应用[J].矿床地质,2006, 25(1):27-35.

[2]青海省地质矿产局.青海省区域地质志[M].北京：地质出版社,1991.

[3]《中国地质图集》编委会,马丽芳.中国地质图集[M].北京:地质出版社,2002.

[4]潘彤.青海省金属矿产成矿规律及成矿预测[M].北京:地质出版社,2006.

[5]迟清华,鄢明才.应用地球化学元素丰度数据手册[M].北京:地质出版社,2007.

[6]Taylor S R.M cl.ennan S M.The significance of the rare earths in geochemistry and cosmochemistry[A].Am sterdam:Elsevier.1986,479-485.

[7]黎彤.化学元素的地球丰度[J].地球化学,1976,(3): 167-174.

[8]孟宪国,赵鹏大.地质数据的分形结构[J].地球科学,1991, 16(2):207.

[9]成秋明.多重分形理论与地球化学元素分布规律[J].地球科学,2000,25(3):311-318.

[10]Goncalesm A.Characterisation of geochemical distributions using multifractal models[J].Mathematical Geology,2001,33:41-61.

[11]申维.n维自仿射分形及其在地球化学中的应用[J].地质论评,2005,51(2):208.

[12]申维.分形混沌与矿产预测[M].北京:地质出版社,2002.

[13]李长江,麻土华,朱兴盛等.矿产勘查中的分形混沌与ANN[M].北京:地质出版社,1999.

[14]孙忠军.矿产勘查中化探异常下限的多重分形计算方法[J].物探化探计算技术,2007,29(1):54-58.

[15]申维.分形求和法及其在地球化学数据分组中的应用[J].物探化探计算技术,2007,29(2):134-137.

[16]Allegre C J,Lewin E.Scaling laws and geochemical distributions［J］.Earth and Planetary Letters,1995,132:1.

[17]韩东昱,龚庆杰,向运川.区域化探数据处理的几种分形方法[J].地质通报,2004,(4):714-719.

[18]邹林.青海阿尔茨托山地区化探找矿信息的快速识别与综合评价[D].长沙:中南大学,2004.

Comparison of Multiple Methods to Determine the Geochemical Anomaly Threshold

CHEN Jian,LI Zheng-dong,ZHONG Hao,WU Ming-gui
(Mineral Resource Exploration Center of Qinghai Nonferrous Metal Geological Exploration Bureau,Xining 810007,China)

Geochemical anomaly minimum is to distinguish the basic indicators of the background area with the exception of areas,and the abnormal threshold accuracy is directly related with the next prospecting work.This paper selects 1:10000 soil geochemical exploration samples elements from Zhiduo county of Qinghai province, and takes Ag,Cu,Zn,Pb,Bi,Mo and W seven kinds of elements as example to study the geochemical exploration test data by traditional method,85%cumulative frequency method and fractal method.It is suggested that the traditional method obtain a small and scatter abnormal range,which relatively close to the abnormal threshold from the 85%cumulative frequency method.They are of reasonable and objective.With respect to the traditional method,the fractal method identify weak and small abnormal is significant,but the abnormal range is excessive, giving rise to the difficulty of abnormal verification work.When to determine an abnormal threshold,we should combine the actual geological background with the geological data distribution patterns,and use multiple method to delineate the practical and effective anomaly area.

geochemical anomaly;abnormal threshold;fractal;85%cumulative frequency method;Qinghai

P632

A

1672－4135（2014）03－0187-06

2014-03-21

中央地勘基金：青海省治多县多彩地区铜多金属矿普查（2009221002）

陈健（1984-）男,硕士,工程师,2012年6月毕业于东华理工大学，现主要从事野外矿产勘查地球化学工作，E-mail:qhyschenjian@126.com。