机器人避障问题

沈璐璐

（陕西能源职业技术学院，西安，712000）

机器人避障问题

沈璐璐

（陕西能源职业技术学院，西安，712000）

本文主要研究了机器人在一个区域内按照一定的行走规则避开该区域内的十二个障碍物，由出发点到达目标点的最短路径和最短时间路径的问题。首先分析得到行走路径由圆弧和与那些圆弧相切的直线组成。然后将路径中遇到的拐点分解为一个或者两个的情况，并给出了各种情况下路径距离以及切点坐标的求法。最后针对不同的目标点分别建立模型并计算出最短路径距离以及途中直线和圆弧的起点、终点坐标。在此基础上，建立非线形规划模型，利用LINGO求出的最短时间路径。

最短路径;最短时间路径;非线形规划模型;LINGO

0 引言

图1是一个800×800的平面区域，内部有12个不同形状的障碍物。在处有一个机器人，它只能在区域内活动且不能与障碍物碰撞。机器人的行走路径由直线和圆弧组成，其中圆弧是转弯路径，该路径由与直线相切的圆弧组成，也可以由两个或多个相切的圆弧组成，但每个圆弧的半径最小为10个单位。同时机器人行走线路与障碍物间的最近距离为10个单位。机器人直线行走的最大速度为个单位/秒，最大转弯速度为是转弯半径。障碍物的数学描述如下表：

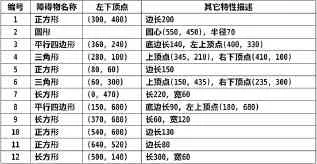
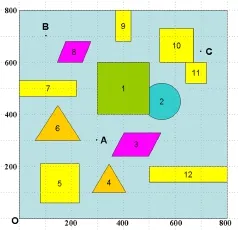
图1

1 模型分析与求解

1.1 问题一

根据行走规则，画出行走过程中的危险隔离线，每到拐点处，隔离线都为半径为10的圆弧。不难发现，起点到目标点的路径中不管障碍物有多少，最短的路径都应该是若干半径为10的圆弧和与那些圆弧相切的直线组成。此问题中求的最短路径中遇到的拐点要么为1个，要么为多个，对于不同个数的拐点分情况讨论如下。

（1） 一个拐点：

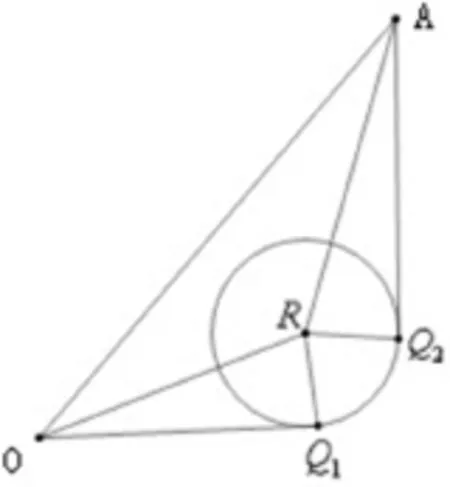
图2

（2） 多个拐点：多个拐点可每次只考虑两个拐点，最后再相加。两个拐点的情况可分为图3和图4两种。

图3

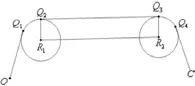
图4

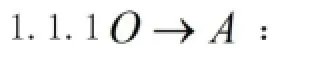
从O到A有两条路径，如图5。

图5

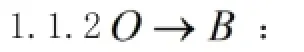
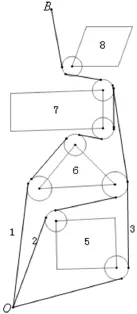
图6

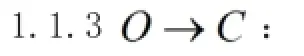
1.2 问题二

2 模型的评价

本模型全面考虑了出发点到目标点的可行路径，并选择出几条可能的最短路径，分情况讨论并计算出各条路径的距离，最终比较得出最短路径，结果精确度较高。并建立非线形规划模型求解出从出发点到目标点的最短时间，简单易懂，利用软件求解，精确度高且费时少。但是当障碍物较多或者障碍物形状，本模型还需进一步改进，寻找更高效的方法。

[1] 机器人行走问题, http://wenku.baidu.com/ view/606c2a094a7302768e99399a.html.

[2] 谢金星，薛毅，优化建模与LINDO/LINGO软件[M]，北京：清华大学出版社，2005.

[3] 韩中庚，数学建模方法及其应用[M]，北京：高等教育出版社，2005.

公式1：

The robot obstacle avoidance

Shen Lulu
(Shaanxi Energy Vocational and Technical College,Xi’an,712000,China)

This paper studies the shortest path and the shortest time path problem from the starting point to the target point in a region with twelve obstacles,the robot walks in that area according to certain rules to avoid those obstacles.Firstly,the walking path constituted by some arcs and straigt lines tangent to those arcs.The path can be decomposed into one or two inflection points,then gives solving methods of the path distance and tangent point coordinate in various situations.Finally,for different target points,models are established and calculates the shortest path distance and the starting and ending points coordinates of the straight lines and arcs.On this basis,a non-linear programming model is established, and the shortest time path form O to A is solved by LINGO.

The shortest path;The shortest time path;non-linear programming model;LINGO