电力市场中一类博弈模型的脉冲延迟反馈控制法

王国栋

到现在为止，人们对非线性动力系统的研究有很多［1－5］，而脉冲动力系统的研究在过去几十年成为人们研究的主要对象.通过研究发现，脉冲动力系统可以提供现实世界中某些瞬间变化的自然进化过程中的数学模型.最近学者们对经济动力系统的研究往往会在微分方程中加入时间延迟因素［6］，而一般的微分方程并不能全面描述一些经济现象.动态的经济变量存在时滞的原因有:(1)做出的经济决策与决策发生效力之间存在时间延迟;(2)经济代理人被认为是完全理性的.完全理性博弈是基于两个假设前提:一是每个发电商在决策时，都具有完备的信息;二是每个发电商都是基于完全理性进行决策的.在现实中，发电商之间的博弈是不断进行的，不可能立即达到Nash均衡状态，同时每个发电商掌握的信息都是不充分的，而且发电商决策都是由人做出的，而人的决策也不可能是完全理性的，只能是有限理性［7］.

1 模型的建立

假设市场由两个区域市场组成，记发电商团队为A、B，每个投资方的战略空间是选择投资的发电量，利润是支付，发电商团队A 是有2 个合作的发电商1 和发电商2 组成，团队B 中只有1 个发电商3.假设发电商1 和发电商2 均为有限理性调整型，发电商3 是自适应调整型，且他们的逆需求函数均为非线性的，即

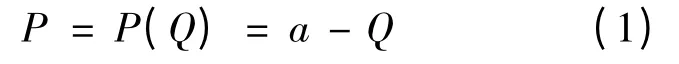
其中ai，bi，ci＞0，a 为非负参数.发电商1 和2是合作关系，存在技术价格情报共享等.不妨假设a1=a2，b1=b2，c1=c2.合作的团队往往是出于共同的利益来选择合作，而发电商之间实力的差异，必然存在利益的分配问题，团队A 中发电商1 和发电商2 的利益分配权重分别为w 和1－w，团队A 和团队B 的利润函数πA和πB分别为:

其中0 ＜w ＜1.在实际电力市场中，每个发电商并不具有完全的市场信息，也不可能完全预测未来的市场变化情况，因而他们的决策往往基于部分信息而做出.本文假设投资方A 是基于上一时刻的边际利润的基础上做出有限理性调整.如果发电商团队A 认为第t 时刻边际利润为正，则他将会在第t+1 时刻增加发电量;反之如果边际利润为负，他就会减少发电量.于是可得到发电商1 和2 在第t +1 时刻的发电量为:

式中:i=1，2 ;αi＞0 为调整率.发电商3 是根据t 时刻自身的发电量以及竞争对手t 时刻的反应发电量

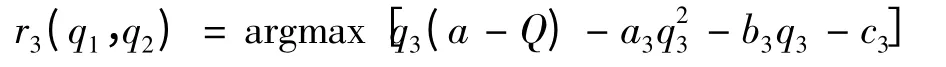
并给予比例来决t +1 时期的发电量.具有如下形式:

可以得到发电商在t +1 时刻的投资模型

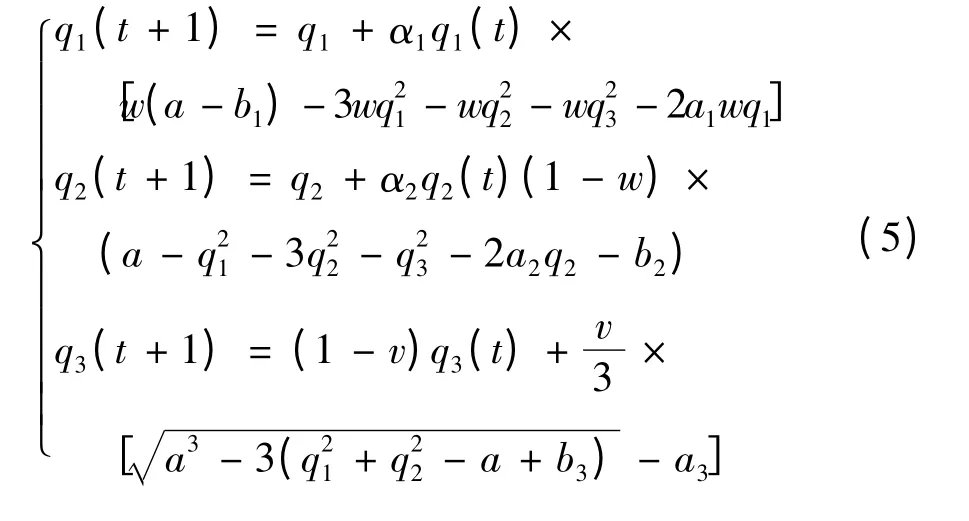
2 模型的分析

2.1 投资商1 加入时间延迟反馈控制

由前面的研究可以知道，当参数取

a=15，w=0.28，α2=0.2，a1=5，a2=6，b1=b2=c1=c2=0，v=0.5 系统会出现混沌现象.为了防止系统进入混沌状态，我们可以加入时间延迟的方法来控制.

μ(t)= ω(x(t +1－T)－ x(t +1))，t ＞T T 为延迟时间，ω 为控制系数.

如果我们对有限理性投资者A 加入时间延迟决策，则控制系统(5)改写为:

我们选择T=1，控制系统(6)可以表示为

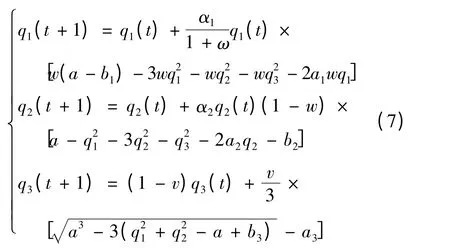
则系统(7)的Jocobian 矩阵为:

将混沌参数

a=15，w=0.28，α1=0.75，α2=0.2，

a1=5，a2=6，b1=b2=c1=c2=0，v=0.5，

则Jocobian 矩阵变为:

根据Jury 条件，通过计算得出，且仅当ω ＞0.646 7，也就是说当ω 满足ω ＞0.646 7 时，系统的特征值是小于1 的，系统是围绕Nash 均衡点稳定的.

当取参数a=15，w=0.28，α2=0.2，a1=5，a2=6，b1=b2=c1=c2=0，v=0.5，系统出现混沌状态，如图1所示.

在系统中引入时间延迟反馈控制参数后，取参数a=15，w=0.28，α1=0.75，α2=0.2，c1=5，c2=6，v=0.5，系统变得稳定，如图2所示.

图1 投资商2 的时序图

图2 系统7 的投资量时序图

2.2 整个系统引入时间延迟反馈控制

由于投资市场信息的不完全性，以及投资者行为有限理性，为达到投资系统共同控制混沌的效果，3 个投资商均采用时间延迟反馈控制，则系统可以改写为系统(8)

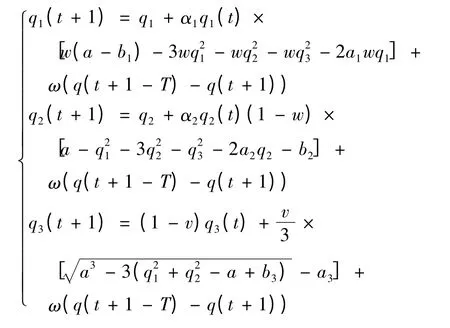
令T=1，则系统(8)变为系统(9)

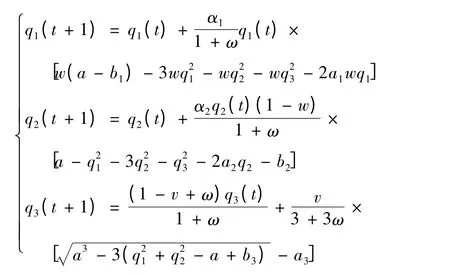
上式的Jocobian 矩阵为:

将混沌参数

a=15，w=0.28，α1=0.75，

α2=0.2，a1=5，a2=6，

b1=b2=c1=c2=0，v=0.5

可以求得Jocobian 矩阵为:

根据Jury 条件，系统如果要保持稳定而不进入混沌状态，通过计算可以得出;当且仅当ω ＞0.482 7 时，系统(9)的所有特征值都小于1，说明系统是围绕Nash 均衡点稳定的.意味着离散的动力系统即投资系统在满足时间延迟反馈控制系数ω ＞0.482 7 时，3 个投资商是稳定共存的.如图3，图4分别表示一家投资商加入时间延迟反馈控制与3 家投资商都加入时间延迟反馈控制.

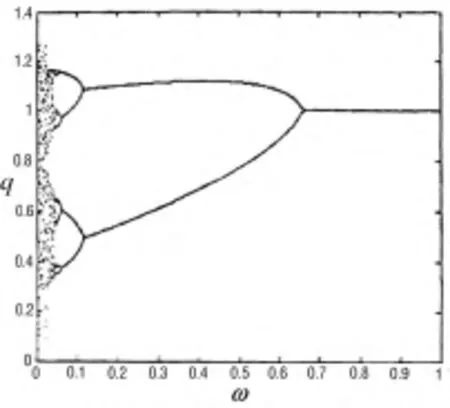
图3 一家投资商加入时间延迟反馈控制

图4 三家投资商加入时间延迟反馈控制

由图3与图4的比较，可以看出，当只有一家投资商加入时间延迟反馈控制，反馈参数只有满足ω ＞0.646 7 时，系统才达到Nash 均衡稳定，当3 家都加入时间延迟反馈控制时，反馈控制参数只需要满足ω ＞0.482 7 时，系统就可以达到Nash 均衡.也就是说3 家投资商均采用时滞延迟控制的方法比只有一家采用时滞延迟控制更能有限快速的达到混沌控制的目的.

3 结语

本文在电力市场中建立一类含差异化策略的博弈模型，针对模型出现的混沌状态，在系统中加入时间延迟反馈控制参数，对系统进行控制，还就一家投资商加入时间延迟反馈参数与3 家同时加入时间延迟反馈控制参数利用非线性理论进行分析，这两种控制方法都成功使原来不稳定的系统达到稳定状态，且3 家投资商同时加入延迟反馈控制参数要比其中一家加入延迟反馈控制参数更快达到稳定状态.

［1］ 姚洪兴，潘红.一类含脉冲延迟反馈金融系统的稳定性分析［J］.江苏大学学报，2011(3) ：32 －34.

［2］ 姚洪兴，王娜娜.含时滞的企业竞争动力系统模型稳定性分析［J］.江苏大学学报，2010(3) ：31 －33.

［3］ 姚洪兴，张芳.差异化策略的两组动态古诺模型的分析［J］.江苏大学学报：自然科学版，2012，33：365－368.

［4］ Chian A C L，Borotto F A，Rempel E L，et al.Attractor merging crisis in chaotie business eyeles［J］.Chaos Solitions，2005(24) ：869 －875.

［5］ Chian A C L，Rempel E L.Rogers complex economic dynamics chaotic saddle crisis and intermitteney［J］.Chaos Solitons，2006(29) ：1194 －1218.

［6］ Chen W C.Dynamics and control of finanes system with time－delayed feedbacks［J］.Chaos Solitons，2008(37) ：1198 －1207.

［7］ 姚洪兴，徐峰.双寡头有限理性广告竞争博弈模型的复杂性分析［J］.系统工程理论与实践，2005(12) ：22 －28.