拓展型Horava 引力的解

陈希明，李树晨

最近，一种Power －counting 可重整的紫外完整的引力理论被Horava 提出［1－4］.尽管该理论具有红外固定点，即广义相对论，然而在紫外波段该理论的固定点在时空中具有各向异性:xi→lxi，t →lzt，这里l，z，xi和t 分别是缩放因子、动力学的临界指数、空间坐标和时间坐标.然而，最新的进展表明了由Horava 给出的作用量不具有一个良好的红外行为.由于该理论违反全时空的微分同胚不变性，故在红外时理论具有会产生一个额外的不稳定标量模，并会引起强耦合问题.根据Blas 等人的观点［5］，这个数学模型的一些项似乎需要被修改从而来避免强耦合问题、不稳定问题、动力学不自洽问题和非物理的额外模.他们从低能角度出发讨论了Horava 模型的自洽性.他们发现，额外的标量自由度明显破坏了广义协变性及其他相关特性.这个新模型的一个反常特征就是它满足动力学方程的一阶关系(对时间求导).在线性近似下这个额外的自由度只表现在非静态空间下的不均匀背景中.他们发现了两个跟这个模型相联系的严重问题:首先，这个模型在短距离内表现出它的指数不稳定性的增长;其次，它在一个极端的低临界尺度下变为强耦合.

最近，文献［6］提出了一个新的Horava 引力的拓展理论，它是基于以下的3 个条件:(Ⅰ)紫外完备;(Ⅱ)良好的红外行为，以及(Ⅲ)量子化后具有稳定的真空状态.这个拓展的理论具有Power－counting 可重整性并且可以避免强耦合问题.

在文献［8］中Lu 等人推导出了Horava 引力的动力学方程的完整形式，并且他们同时得到了静态的球对称的解.那么在现在的这篇论文中，我们希望从这个新版本的Horava －Lifshitz 引力的框架下得到静态的球对称解.

1 Horava 引力的整体框架

我们从文献［6］中给出的作用量开始求解.

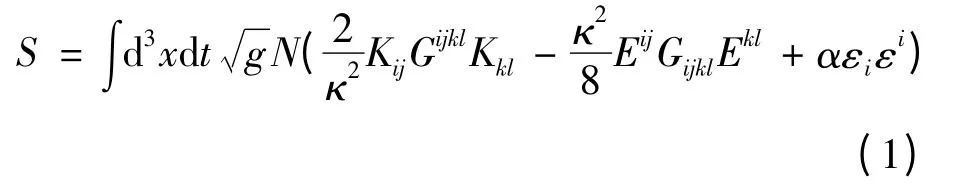
这里Kij和Eij分别用以下形式给出:

而

其中

而μi(i=1，2)是标度量纲为［μi］s=i - 1 和［ΛW］s=2 的耦合常数.在公式(1)中的3 维矢量εi是以这样的形式给出的:

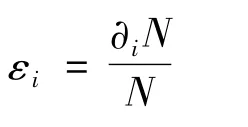
作用量(1)可以被重写为

其中

而且

这里μ，ω 和ΛW是常值参数，而对称张量Zij=是由Ricci 张量和Cotton 量Cij构成的，其中Cij被定义为

2 场方程

我们来考虑作用量(5)的动力学方程.这个由变化的N，Ni得到的动力学方程分别由以下形式给出:

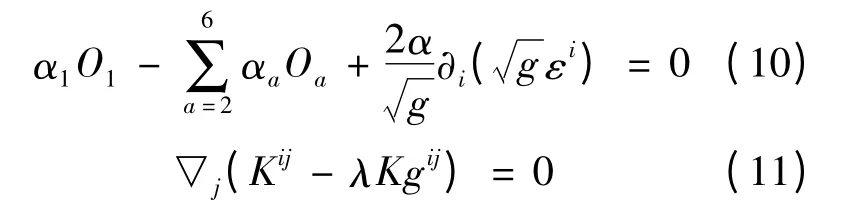
由δgij的变形体而得到的动力学方程被如下公式给出:

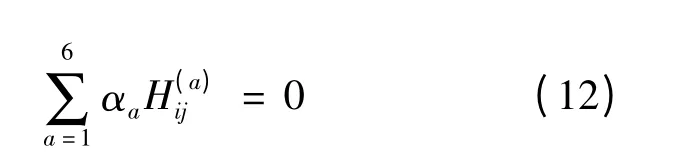
当α3=0 时，这些动力学方程就减少到文献［7 －8］中的几个原始的场方程.

3 静态的球对称解

我们假设理论具有以下形式的静态球对称解:

文献［8］表明在α3=0 情况下的场方程的系统具有(A)dS Schwarzschild 黑洞.作为在旧版本的Horava 引力下的一个常用的方法，在α3≠0 的情况下得到完整拉格朗日量的解的最容易的方式就是把这个度规拟设替换进作用量，然后对函数N 和f 变分.这是一个有效的程序，因为这个拟设包括了所有允许存在的与在S2上的SO(3)作用量相容的单线态粒子.由此产生的缩减的拉格朗日量，相当于一个完整的度量常数，它被如下给出:

A.精确解:第1 类

第一个解按如下给出:

这是一个AdS2× S2时空的表示，这里时间坐标被重调为该解有一个Ricci标量奇点位于:

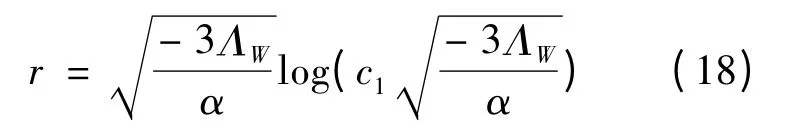
这个解渐渐地接近AdS4.若固定:

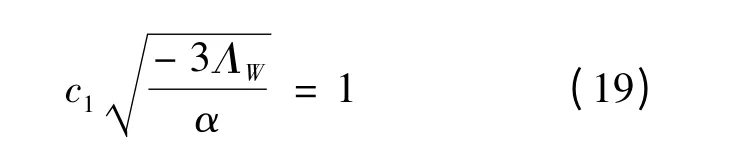
则可以看出该奇点位于r=0，它是一个坐标奇点而非裸奇点.此时度规变为:

图1 ln随径向坐标x 的变化

牛顿势gtt=- N(x)2有一个最大值落在(x=0，gtt=1.253 41)，这意味着我们也许会有一个从原点而来的最大红移.这就使我们有必要去探究引力红移的行为.运用通常的红移公式，我们发现:

我们把红移的变化作为x 的一个函数进行作图，如图2所示.图中所示的位于点x=1.246 附近的红移发散行为可以被认为是由于视界的存在所引起的引力红移.

图2 从x=0 的原点处发出的光子的红移随x 的变化

B.当λ=1 的情况

探究λ=1 这个解是特别有趣的，在此情况下，f 和N 的函数具有如下形式:

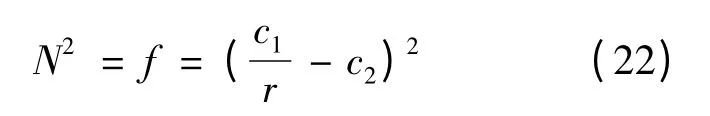
这个解是渐进平坦的，它有一个在r=h 的视界，这里h 是f 的根，其值为

显然，视界处具有零温.在这种情况中的精确解可以被重新写为:

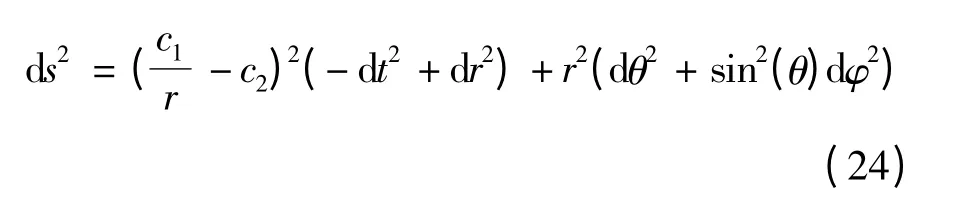
正如我们注意到的那样，这个解是渐进平坦的.那么，用在渐进平坦时空中的引力红移的常规公式我们就有

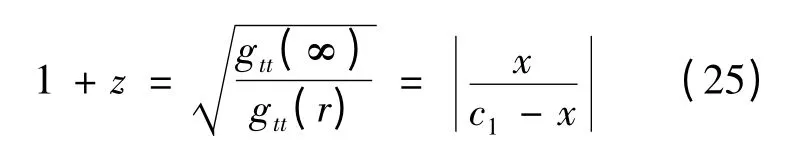
这里x=c2r.这个奇点落在x=c1处.要使r →∞时时空是回到Minkowski 时空，我们有:c2= 1.未定的参数c1=a 可以看作是这个时空的质量.在下文中，我们把红移作为坐标x 的函数针对于a 的一些典型值做了图像.图中显示了该红移在a 取不同值的情况下相对于坐标x 的变化行为.

图3 从原点发出光子的红移对视界值a 的关系

正如我们所观察到的那样，对于a 的这些不同取值该红移产生了数次极大值

C.当ΛW=0 的情况

在这种情形f 和N 都是确定的，由下式给出:

这里β 是一个积分常数.为了使这个解有意义，我们要求λ ＞1.这个解对于一般的λ，当r=0时有一个曲率奇点，这与早先的解有类似的规律［8］.当β ＞0 时，这个解在x=∞处也有一个曲率奇点.此时精确解可以写成:

对于一些β 和γ±的值，当γ±=- β 时这个解(28)就转换成一个共型稳态解:

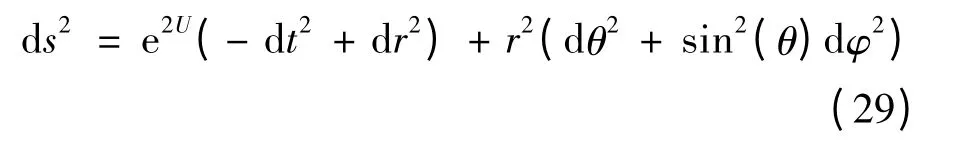
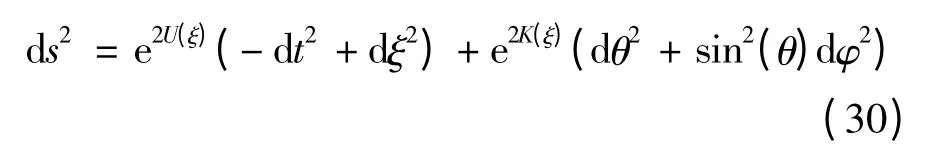
这里

图4 牛顿势eU(ξ)

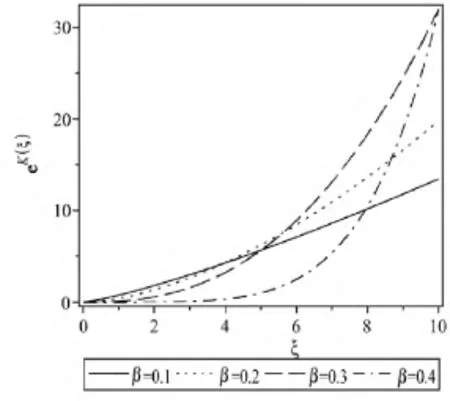
图5 牛顿势eK(ξ)

4 结论

原始形式的Horava 引力必须被修改才能给出正确的预测.在旧版本的Horava 理论中的重要问题之一就是它的Lapse 函数不是动力学的.这个问题可以通过在作用量中插入一个新的辅助场然后探究它的动力学行为来解决.在本文中，以文献［6］中所提出的理论新版本为出发点，我们研究了这个新版本下的球对称解.我们得到了3 种不同类型的解.它们的作图分析表明这些解可以被当作是黑洞的解.部分关于这些解的奇点结构的标志也被探讨.

致谢:非常感谢南昌大学物理系舒富文教授在本论文创作过程中给予的有益讨论和支持及指正.

［1］ Horava P.Quantum criticality and Yang – Mills gauge theory［J］.Phys.Lett.B，2010，694(2) ：172 －176.

［2］ Horava P.Membranes at quantum criticality［J］.JHEP，2009(3) ：20.

［3］ Horava P.Quantum gravity at a Lifshitz point［J］.Phys.Rev.D，2009，79(8) ：84008.

［4］ Horava P.Spectral dimension of the universe in quantum gravity at a Lifshitz point ［J］.Phys.Rev.Lett.2009，102(16) ：161301.

［5］ Blas D，Pujolas O，Sibiryakov S.On the extra mode and inconsistency of Hoˇrava gravity［J］.JHEP，2009(10)：29.

［6］ Shu F W.Extended Hoˇrava gravity with physical ground－state wavefunction［J/OL］.(2010 －09 －20) ［2013－12 －25］.http：//arxiv.org/abs/1009.3677.

［7］ Kiritsis E，Kofinas G.Horava －Lifshitz cosmology［J］.Nucl.Phys.B.2009，821(3) ：467 －480.

［8］ Lu H，Jian Weimei Pope C N.Solutions to horava gravity［J］.Phys.Rev.Lett.2009，103(9) ：91301.