爆破冲击荷载作用下中隔墩岩体的动力响应与局部破坏机制
张 乐 ,卢文波,周俊汝,胡英国,陈 明,严 鹏
(1.武汉大学 水资源与水电工程科学国家重点实验室,武汉 430072;2.武汉大学 水工岩石力学教育部重点实验室,武汉 430072)
1 引言
在水利水电工程施工中,由于两侧进行深槽爆破开挖,常常形成一个中部由保留岩体组成、两侧具有直立边墙的墩体结构,称之为中隔墩。根据建筑物的功能要求,中隔墩在开挖完成后往往形成至少3个临空面,在结构上起到了“分离、隔断”的作用。
中隔墩两侧深槽开挖的一般程序是:首先,在中隔墩两侧的开挖线上进行预裂爆破,然后,两侧岩体大体平行地分层向下开挖至建基面。由于各种因素的影响,中隔墩一侧深槽先于另一侧开挖,造成两侧深槽不能同步下降的局面,如大渡河沙坪二级水电站导流明渠右岸预留岩坎的爆破开挖,见图1(a),三峡工程临时船闸与升船机的开挖[1],见图1(b),又如地下厂房三大洞室平行开挖过程出现的邻洞爆破对已形成的高边坡稳定性影响[2-3],见图1(c)。由于中隔墩一侧已开挖形成临空面,另一侧深槽爆破开挖诱发的地震波传播到这一临空面时将发生反射,反射产生的拉应力使中隔墩产生拉裂破坏,在近临空面处形成岩体松动带,不利于保留岩体的局部稳定,如图1 所示。
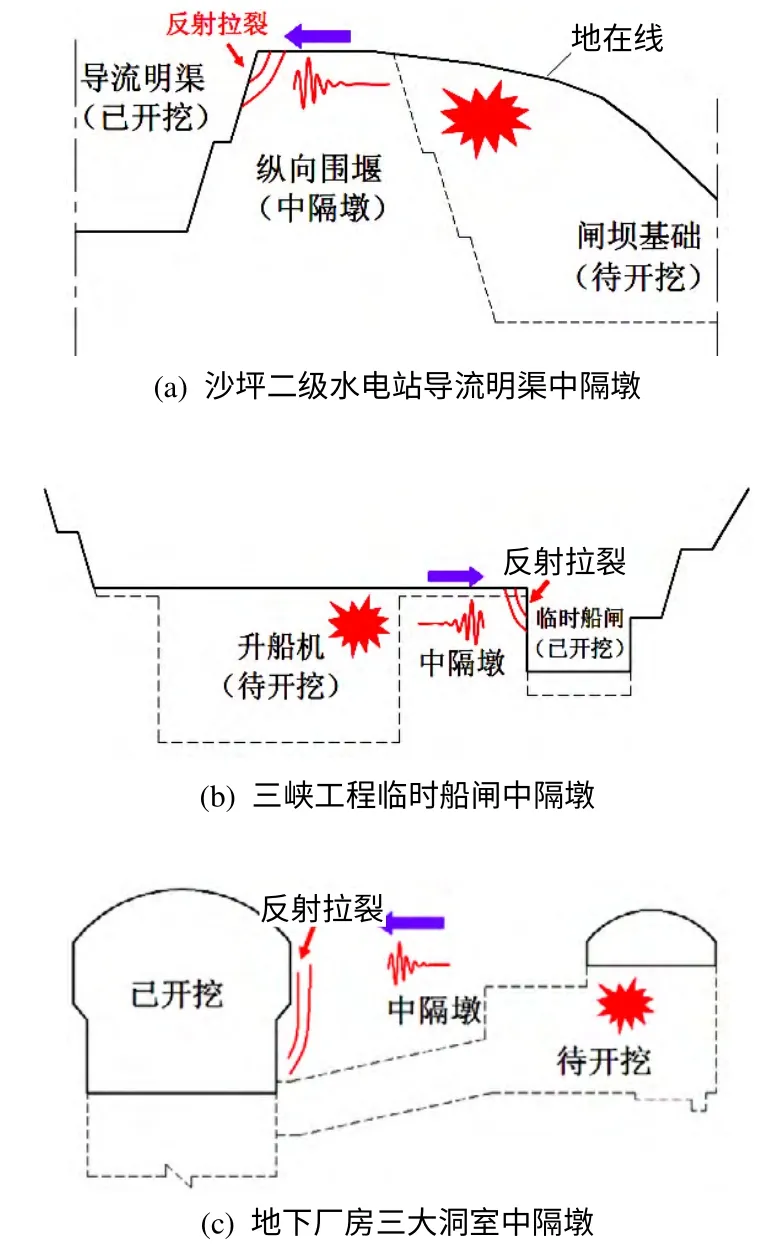
图1 开挖过程形成的岩体中隔墩Fig.1 Division pier formed during excavation process
就三峡工程临时船闸中隔墩而言,升船机右侧预裂爆破过程中因右传的爆破地震波会在中隔墩的临时船闸侧直立边墙上发生反射,从而使其墩顶上的爆破振动分布自升船机侧边缘向右逐渐衰减,至临时船闸侧边缘的一定范围内又发生局部放大[4],如图2 所示。
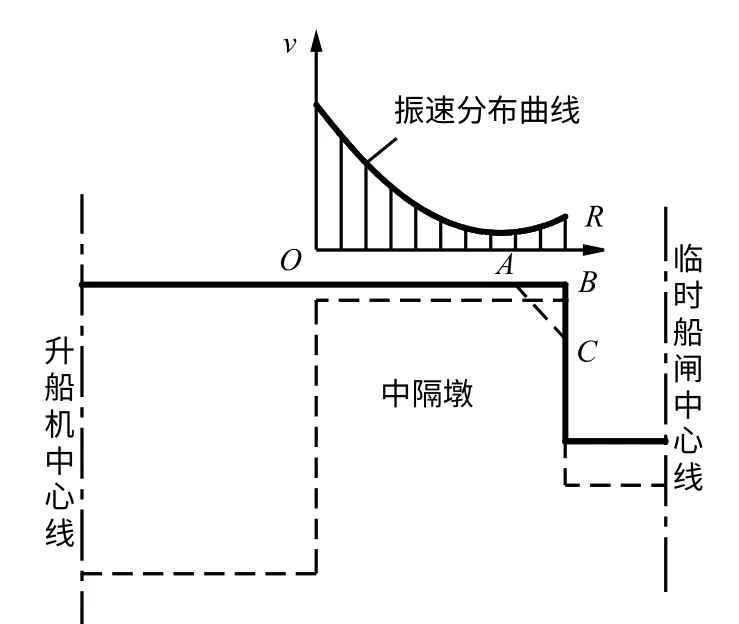
图2 中隔墩墩顶的振速分布Fig.2 Distribution of vibration velocity on the top of division pier
由于爆破振动在中隔墩的临时船闸侧顶边缘处的放大,再加上岩体的自重、开挖引起的卸荷与松动的影响,图2 中ABC 范围的岩体往往会发生局部掉块或坍塌。
针对爆破应力波作用下岩体的稳定与破坏方面,Field[5]和Bhandari[6]分析了爆破破岩过程中应力波与准静态气体压力的作用。Talhi 等[7]利用爆破试验讨论了爆破与分段参数及P 波峰值应力之间的关系。Ahmed 等[8]指出隧洞围岩与喷射混凝土衬砌的相互作用是由于应力波的传播,采用数值模拟方法分析混凝土衬砌与围岩交界面的应力响应。
针对三峡工程临时船闸与升船机开挖,朱传云等[1]在现场试验和研究的基础上确定了爆破振动速度控制的安全判据。卢文波[4]基于中隔墩岩体动力稳定性和爆破损伤的定性分析,提出了三峡工程临时船闸与升船机部位的合理开挖方式及程序。在该工程实例中得到的重要认识,即采用具有侧向临空面的预裂爆破可以有效地将爆破能量向预留岩体转移,从而保证中隔墩岩体的安全与稳定。但是,对于有侧向临空面预裂爆破时机选择,尤其是预裂爆破前预留的岩体厚度理论计算和局部失稳破坏的定量分析方面尚有待开展进一步研究。
本文以三峡工程临时船闸与升船机的开挖为实际工程背景,针对爆破冲击荷载作用下中隔墩岩体的动力响应和局部破坏机制开展进一步研究,确定了预留岩体厚度以及预裂爆破时机,为爆破开挖程序和方案优化提供依据。
2 中隔墩岩体的动力响应
应力波在传播过程中若遇到自由面会发生反射,假定入射应力波记为
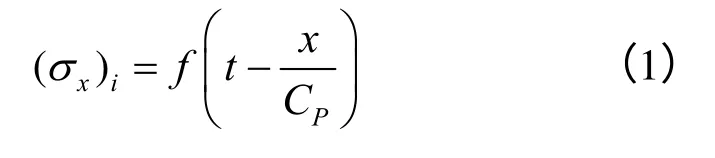
在自由边界x=a 处,应力为0,于是,反射应力波可以表示为
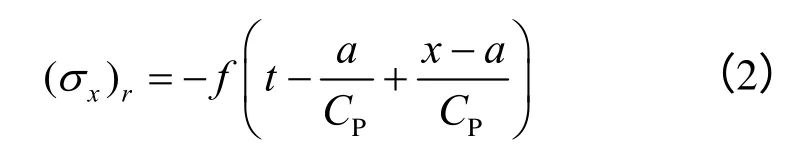
式中:CP为纵波波速,其表达式为

式中:ρ为介质密度;λ、μ为拉梅常数,

方程式(2)表明,反射应力波与入射应力波有相同的形状,但应力的符号在反射后改变。
2.1 计算模型与参数
升船机的爆破开挖对中隔墩带来的不利影响首先来自升船机右侧开挖边线上的预裂爆破,因其较之升船机主爆孔的梯段爆破,离中隔墩更近,且爆破作用力正冲中隔墩,加之多孔同时起爆的要求致使单段药量较大。为了直观地说明升船机右侧开挖线上的预裂爆破对中隔墩产生的不利影响,本文运用动力有限元分析软件ANSYS/LS-DYNA 进行数值模拟计算,分析中隔墩在预裂爆破冲击荷载作用下的动力响应,计算模型见图3。
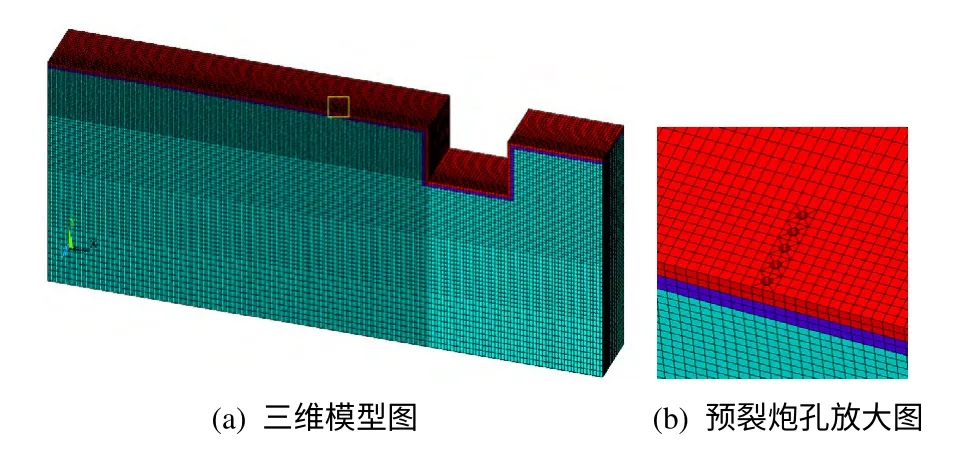
图3 动力有限元模型Fig.3 Dynamic finite element model
建模过程中,将岩体简化为各向同性的均匀介质,岩体本构模型采用塑性随动模型(*MAT_PLASTIC_KINEMATIC)。同时,为考虑历史爆破开挖对保留岩体产生的损伤,对模型表面的岩体参数进行了折减,共分2 层折减,每层1 m。取中隔墩宽度为30 m,左侧待开挖岩体宽度为3 倍中隔墩宽度,已开挖侧深槽宽为25 m,深19 m。模型X 方向总长175 m,Y 方向高79 m,Z 方向宽20 m,共570 150个单元。预裂炮孔5 孔一段,孔径为90 mm,孔深19 m,孔间距1 m。爆破荷载以荷载曲线的形式施加在炮孔的弹性边界上。模型侧面及底面施加法向位移约束,边界设为无反射边界以反映岩体的实际受力状态,岩体参数见表1。

表1 岩体力学参数Table 1 Mechanical parameters of rock mass
为了简化计算,将爆破荷载作用型式简化为三角形[9-12],如图4 所示。图中,t1=3 ms,t2=12 ms,P0=25 MPa。
2.2 计算结果分析
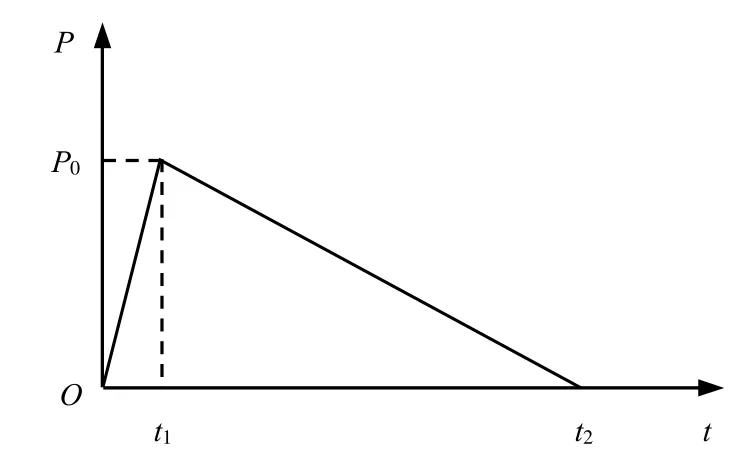
图4 爆破荷载曲线Fig.4 Curve of blasting load
基于上述模型,取预裂炮孔两侧(已开挖方向与待开挖方向)的计算结果进行对比分析。由应力波理论可知,质点峰值振动速度与岩体的动应变或动应力间存在对应关系[13],而位移是岩体变形最直观的反应,故本文取X 方向拉应力峰值、质点峰值振动速度及位移结果分析中隔墩的动力响应,如图5~7 所示。
由图5为预裂炮孔两侧X 方向拉应力峰值随爆心距的变化对比曲线可以看出,当爆心距小于15 m范围内时,中隔墩两侧的X 方向拉应力峰值几乎一致;当爆心距大于15 m 时,两侧的拉应力峰值开始分离,尤其是在近临空面处,已开挖方向的应力峰值明显大于待开挖方向,并在爆心距26 m 处,两者相差最大。图6、7 分别以速度和位移作为指标,由图可以看出,在爆心距18 m 以内,中隔墩两侧的峰值振速基本一致;当爆心距大于18 m 时,两侧的峰值振速开始分离,并在临空面处相差最大,可见临空面对爆破振动具有放大效应,已开挖侧的位移在全高程上均大于待开挖侧。
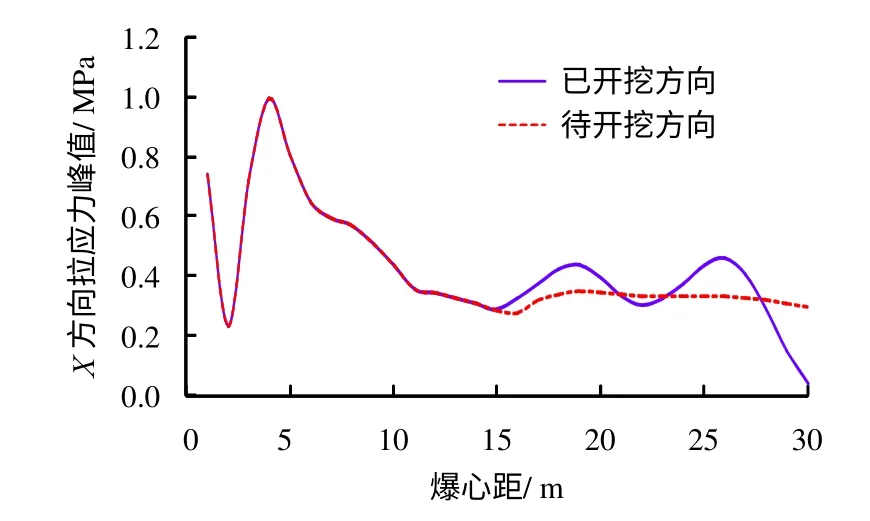
图5 预裂炮孔两侧X 方向拉应力峰值Fig.5 Peak tensile stress in X-direction on both sides of pre-splitting hole

图6 预裂炮孔两侧X 方向峰值振速Fig.6 Peak velocity in X-direction on both sides of pre-splitting hole
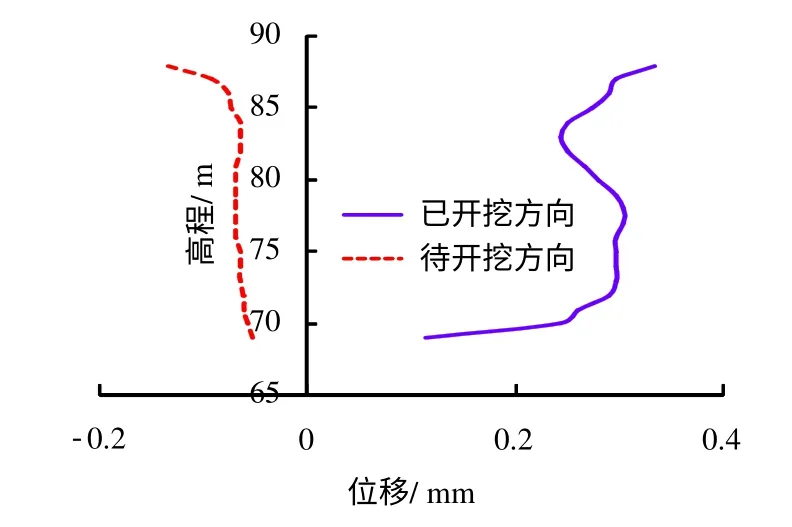
图7 预裂炮孔两侧爆心距30 m 处位移随高程的变化Fig.7 Variation of displacement with elevation on both sides of pre-splitting hole 30 m away from blast center
由以上分析可知,由于临空面的存在使中隔墩已开挖侧岩体的动力响应明显大于待开挖侧,故需对升船机的爆破开挖方案进行优化以保证中隔墩的稳定与安全。
三峡工程临时船闸与升船机部位岩体开挖施工过程,通过理论分析和现场实验,采用了具有侧向临空面的预裂爆破方式,其爆破开挖程序为:先在待开挖深槽进行抽槽爆破以形成临空面(I1);后逐步往中隔墩方向扩挖(I2),当扩挖至剩余岩体的厚度达到中隔墩岩体厚度的1/3 左右时,再在中隔墩待开挖侧开挖线上进行预裂爆破(I3);最后,用常规的梯段爆破技术将所剩岩体爆除(I4),如图8 所示。由文献[4]可知,该开挖程序与方案最终获得了成功。
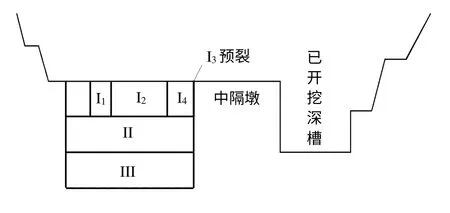
图8 开挖程序示意图Fig.8 Sketch of excavation procedure
3 预裂爆破的时机选择
为了进一步确定待开挖侧预留岩体厚度的最优值,直接将章节2 中的模型进行分步开挖,分别得到预留岩体厚度为30、20、15、10 m 及5 m 五种开挖模型,在以下分析与描述中,将简单地以每种开挖模型的剩余岩体厚度作为各自的名称。图9为预留岩体厚度为10 m 的三维模型图。
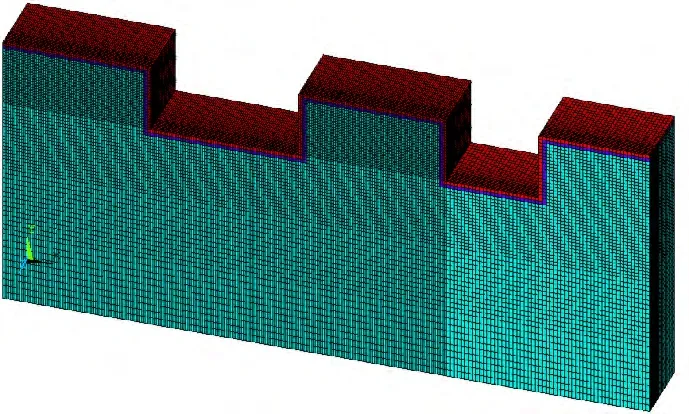
图9 预留岩体厚度为10 m 的三维模型Fig.9 3D model of 10 m thick reserved rock
图10为不同预留岩体厚度下X 方向拉应力峰值随爆心距的变化对比曲线。由图中可见,除5、10 m 模型外,几种开挖模型与未开挖模型基本重合;而5 m 与10 m 模型表现出较大差异,且5 m模型在近临空面的拉应力值明显大于10 m 模型,说明预留岩体厚度并不是越薄越好,对于中隔墩已开挖侧临空面部分岩体来说,预留岩体厚度10 m最为安全,5 m 反而最危险(30 m 与未开挖曲线重合,故图中未给出,下文如遇同样情况则不再赘述)。
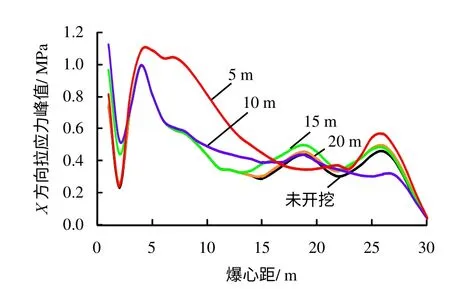
图10 不同预留岩体厚度下X 方向拉应力峰值随爆心距的变化Fig.10 Variation of peak tensile stress in X-direction with blast center distance under different reserved rock thicknesses
此外,如章节2 所述,爆心距26 m 处X 方向拉应力峰值在近临空面达到顶点,故将爆心距26 m作为控制点,图11为爆心距26 m 处各模型X 方向拉应力峰值沿高程的变化对比。从图中同样可以看到,除5、10 m 模型外,几种开挖模型与未开挖模型基本重合;在近顶部临空面处,5、10 m 模型相差较大,且10 m 模型应力值明显小于其他模型。
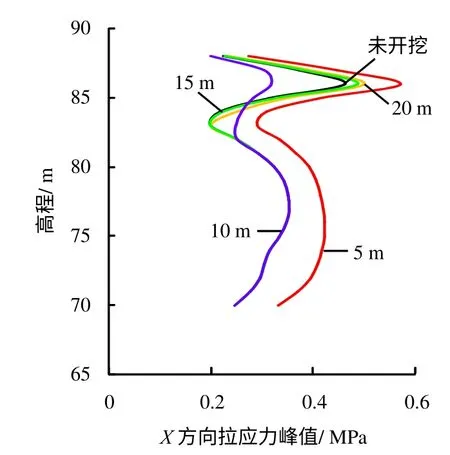
图11 爆心距26 m 处不同预留岩体厚度下X 方向拉应力峰值沿高程的变化Fig.11 Variation of peak tensile stress in X-direction with elevation under different reserved rock thicknesses 26 m away from blast center
从图12、13 可以看出,以速度为指标,同样可以得到预留岩体为10 m 最安全的结论,但以位移为指标,各模型相差不大。
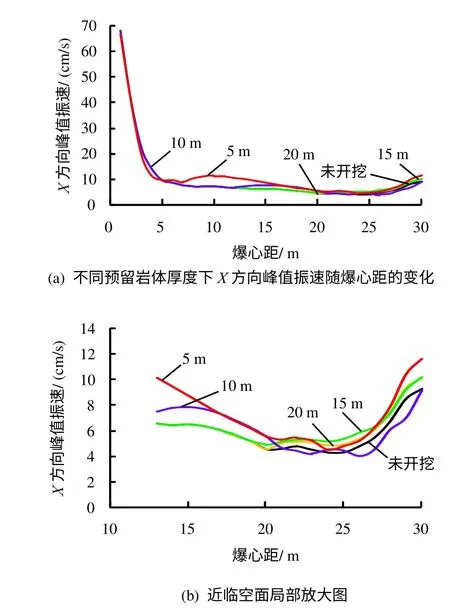
图12 不同预留岩体厚度下X 方向峰值振速随爆心距的变化Fig.12 Variation of peak velocity in X-direction with blast center distance under different reserved rock thickness
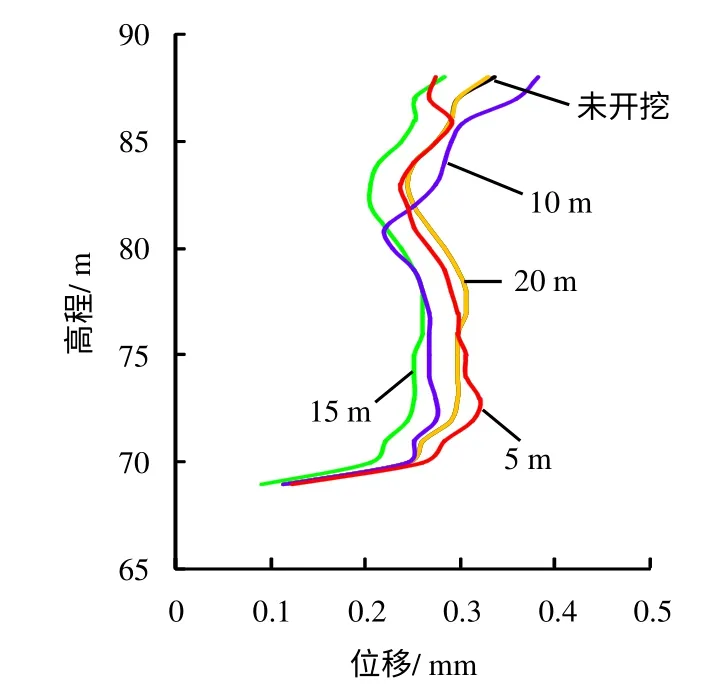
图13 不同预留岩体厚度下爆心距30 m 处位移随高程的变化Fig.13 Variation of displacement with elevation under different reserved rock thickness 30 m away from blast center
为了从整体上分析中隔墩岩体在爆破冲击荷载作用下的动力响应,图14为中隔墩岩体X 方向拉应力峰值的等值线分布图(图中两条相邻等值线的间隔为0.05 MPa)。值得一提的是,由于所涉及的是动力问题,必须考虑时间这一因素。图中的等值线为X 方向拉应力在整个振动过程中曾经达到过的最大值,而不是某一时刻中隔墩岩体的拉应力分布。通过观察可以发现,从整体上来看,10 m 模型应力值较5 m 小且分布较均匀,故预留10 m 的开挖方案更安全。
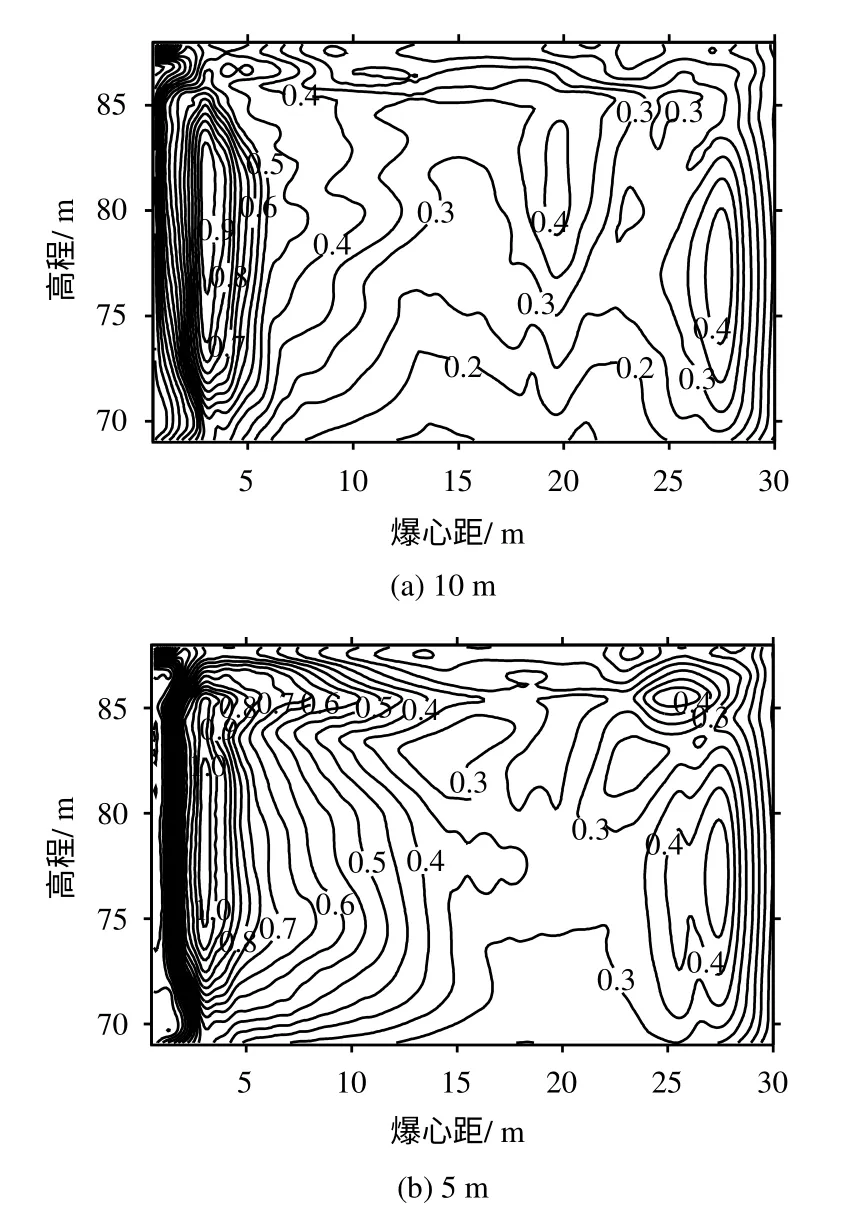
图14 中隔墩内X 方向拉应力分布(单位:MPa)Fig.14 Distribution of tensile stress in X direction in division pier(unit:MPa)
4 应力波的反射与叠加
远离爆源,地震波可以近似看成平面波,由地震波的质点速度可根据式(5)得到地震波的应力:

式中:ρ为岩石密度,由此可知质点应力与质点振速存在一一对应的关系。
由图5 可见,临空面附近X 方向拉应力峰值的最大值出现在爆心距+26 m 处,距临空面4 m。这是由于应力波经临空面反射后与入射波叠加使拉应力峰值增大。下面以爆心距+26 m 作为控制点来说明中隔墩岩体中应力波的反射与叠加以及预留岩体厚度选择的内在原因。
根据波的叠加原理,在波的重叠区域内各点的振动物理量等于各列波在该点引起的振动物理量的矢量和,故将X 方向应力作为研究对象,这样矢量和可以简化为代数和。
以预留岩体厚度10 m(见图15)为例,爆破地震波在爆心距+26 m 处诱发的应力波形应该由3种波叠加而成,分别是爆破地震波传播至+26 m 的入射波形(图中A)、爆破地震波传播至临时船闸自由面后反射并到达+26 m 的反射波形(图中B)以及爆破地震波向左传播至预留岩体自由面后反射并到达+26 m 的反射波形(图中C)。这3 种波形分别与爆心距-26 m 应力波形(图中A′)相等、与爆心距-34 m 应力波形(图中B′)等值异号、与爆心距-46 m 应力波形(图中C′)等值异号。故可以利用未开挖模型预裂缝左侧的爆破数值模拟结果将以上3 种波形提取出来。将A、B、C 三种波形叠加后与10 m 模型+26 m 处波形相比,若两者相符,则说明波的反射与叠加效应是存在的。不同预留岩体厚的结果如图16 所示。
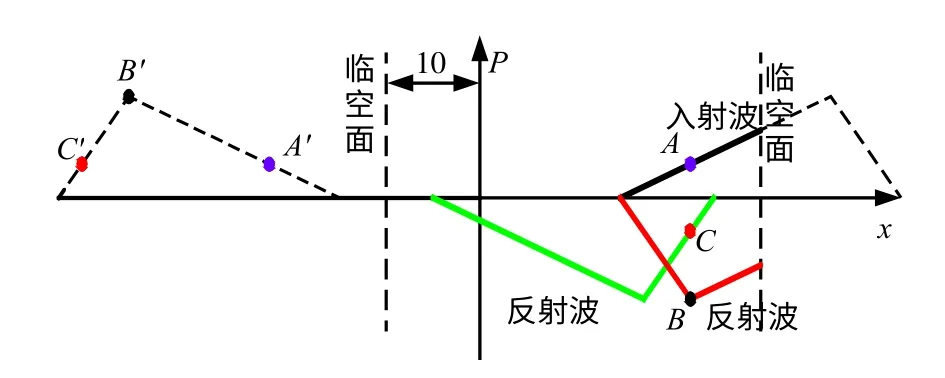
图15 关于入射波与反射波提取的说明Fig.15 Explanation of the extraction of incident wave and reflected wave
在不考虑二次反射的条件下,图16 可以证明波的反射与叠加效应是存在的,且对不同预留岩体厚度下中隔墩爆破开挖的动力响应有重要影响。
首先,为了说明临时船闸临空面对中隔墩的影响,将入射波A和反射波B 提取并比较,如图17所示。从图中可以看到,由临时船闸自由面反射的应力波B 与入射波A 在同一时刻基本上都处于波峰或波谷的位置,应力相互加强,所以说临空面的存在对于中隔墩的稳定的不利的。
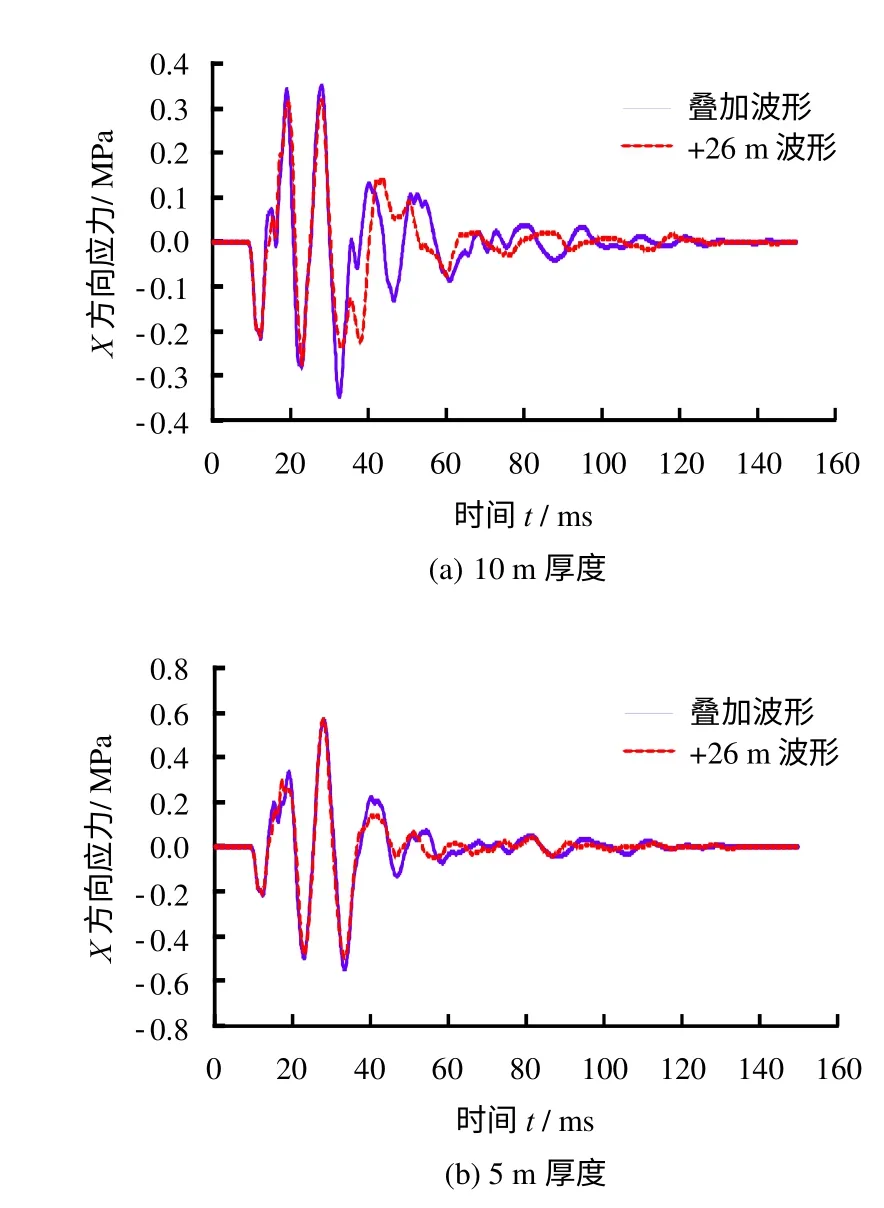
图16 不同厚度预留岩体波的反射与叠加Fig.16 Reflection and superposition of wave under different thickness reserved rock
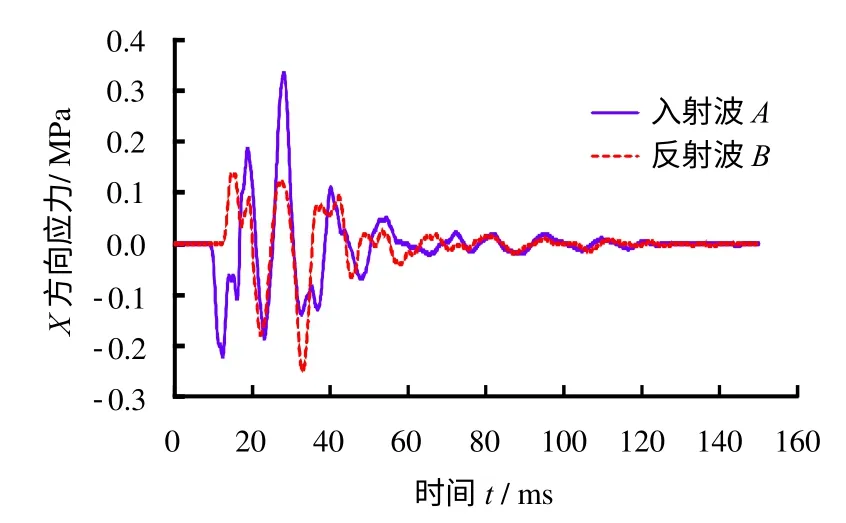
图17 入射波A 与反射波BFig.17 Incident wave A and reflected wave B
另外,为了说明预留岩体厚度选择的内在原因作如下分析:按照如上所述的开挖方案,在中隔墩左侧开挖边线上进行预裂爆破时,预留岩体一侧已形成一临空面,爆破产生的应力波传播到这一边界时会发生反射,反射回来的波将与向临时船闸方向传播的应力波进行叠加。如果正好是波峰与波谷叠加,两者相互抵消,使应力峰值减小;如果正好是波峰与波峰叠加,两者相互加强,使应力峰值增大。
图18 分别为预留岩体厚度10 m 以及5 m 条件下的入射波A 以及反射波C(为了便于分析比较,图中未考虑反射波B)。由图可知,经10 m 厚的预留岩体反射后,反射波与入射波在同一时刻基本上分别处于波峰和波谷位置;经5 m 厚的预留岩体反射后,反射波与入射波在同一时刻基本上都处于波峰或波谷位置。正因如此,中隔墩在不同预留岩体厚度下表现出不同的动力响应。
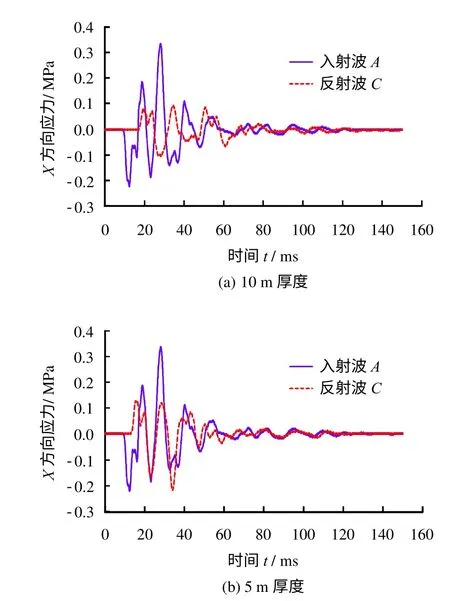
图18 不同厚度预留岩体的入射波A 与反射波CFig.18 Incident wave A and reflected wave C under different thicknesses reserved rock
由文献[14]可知,爆破振动主频在爆心距26 m处约为200 Hz,又由式(3)可知纵波波速为2 500 m/s,计算得波长为12.5 m。设预留岩体厚度为L,那么入射波A 与反射波C 的波程差为2L,根据波的叠加原理:在2 列波叠加的区域内,当波程差为0 或波长的整数倍时,叠加相长(两列波相遇后如果是波峰与波峰叠加,则相互加强);当波程差为半波长的奇数倍时,叠加相消(两列波相遇后如果是波峰与波谷叠加,则相互抵消)。由此可得预留岩体厚度的理论最优值,见表2。
综上可知,波的反射与叠加效应是存在的。由于应力波的反射与叠加效应决定了在不同预留岩体厚度下中隔墩爆破开挖动力响应的大小,通过选取适当的预留岩体厚度,可以合理地利用爆破应力波的反射与叠加,削弱爆破荷载冲击作用下中隔墩的动力响应,进而降低中隔墩因爆破开挖出现动力失稳的风险,可见预留岩体厚度是决定上述开挖方案能否成功的重要参数。

表2 预留岩体厚度理论解Table 2 Theoretical solution of reserved rock thickness
5 结论
(1)若在中隔墩左侧的开挖线上直接进行预裂爆破,由于爆破地震波在自由面的反射,爆破振动会在临时船闸侧边缘处发生局部放大,使临空面附近岩体易发生局部破坏,有必要改善爆破方式,优化爆破程序。
(2)采用先抽槽爆破,再逐步扩挖,最后在预留适当厚度岩体下进行预裂爆破,可以避免爆破能量过多地向中隔墩转移,较好地削减爆破荷载的动力响应。预留岩体的厚度并非越薄越好,计算最优值为10 m,约为中隔墩岩体厚度的1/3。另一方面,预留岩体越薄,意味着在预裂爆破前的扩挖过程中最后一排主爆孔离中隔墩越近,对中隔墩的安全也是不利的。
(3)中隔墩岩体在爆破荷载冲击作用下的动力响应是由于爆破应力波的反射与叠加。通过选取适当的预留岩体厚度,利用爆破应力波的反射与叠加效应,可以削弱爆破荷载冲击作用下中隔墩的动力响应,进而降低中隔墩因爆破开挖出现动力失稳的风险。
以上分析对两侧深槽一侧已开挖形成临空面的中隔墩爆破开挖方式的改善、开挖程序的优化、预留岩体厚度的选取具有重要的指导意义,可供类似工程参考。
[1]朱传云,卢文波.三峡工程临时船闸与升船机中隔墩爆破安全判据的研究[J].爆炸与冲击,1998,18(4):375-380.ZHU Chuan-yun,LU Wen-bo.Blasting safety criterion for the rock wall between temporary shiplock and shiplift in three gorges project[J].Explosion and Shock Waves,1998,18(4):375-380.
[2]LU W B,CHEN M,GENG X,et al.A study of excavation sequence and contour blasting method for underground powerhouses of hydropower stations[J].Tunnelling and Underground Space Technology,2012,29(5):31-39.
[3]XIA X,LI H B,LI J C,et al.A case study on rock damage prediction and control method for underground tunnels subjected to adjacent excavation blasting[J].Tunnelling and Underground Space Technology,2013,35(4):1-7.
[4]卢文波.三峡工程临时船闸与升船机开挖中的爆破方案优化和爆破振动控制[J].岩石力学与工程学报,1999,18(5):497-502.LU Wen-bo.Optimization of blasting procedure and vibration control during excavation of temporary ship lock and ship lift in Three Gorges Project[J].Chinese Journal of Rock Mechanics and Engineering,1999,18(5):497-502.
[5]FIELD J E.The importance of the reflected stress wave in rock blasting[J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts,1971,8(3):213-220.
[6]BHANDARI S.On the role of stress waves and quasi-static gas pressure in rock fragmentation by blasting[J].Acta Astronautica,1979,6(3-4):365-383.
[7]TALHI K,BENSAKER B.Design of a model blasting system to measure peak p-wave stress[J].Soil Dynamics and Earthquake Engineering,2003,23(6):513-519.
[8]AHMED L,ANSELL A.Structural dynamic and stress wave models for the analysis of shotcrete on rockexposed to blasting[J].Engineering Structures,2012,35(2):11-17.
[9]HENRYCH J.The dynamics of explosion and its use[M].New York:Elsevier Scientific Publishing Company,1979.
[10]卢文波,陶振宇.预裂爆破中炮孔压力变化历程的理论分析[J].爆炸与冲击,1994,14(2):140-146.LU Wen-bo,TAO Zhen-yu.Theoretical analysis of the pressure-variation in borehole for pre-splitting explosion[J].Explosion and Shock Waves,1994,14(2):140-146.
[11]阿肯巴赫.弹性固体中波的传播[M].徐植信,洪锦如译.上海:同济大学出版社,1992.
[12]时党勇,李裕春,张胜民.基于ANSYS/LS-DYNA8.1进行显式动力分析[M].北京:清华大学出版社,2004.
[13]卢文波,李海波,陈明,等.水电工程爆破振动安全判据及应用中的几个关键问题[J].岩石力学与工程学报,2009,28(8):1513-1519.LU Wen-bo,LI Hai-bo,CHEN Ming,et al.Safety criteria of blasting vibration in hydropower engineering and several key problems in their application[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(8):1513-1519.
[14]卢文波,张乐,周俊汝,等.爆破振动频率衰减机制和衰减规律的理论分析[J].爆破,2013,30(2):1-6.LU Wen-bo,ZHANG Le,ZHOU Jun-ru,et al.Theoretical analysis on decay mechanism and law of blasting vibration frequency[J].Blasting,2013,30(2):1-6.

